差分约束+模板

标签：code   ++   最长路   printf   stream   差分约束   while   put   技术   

一句话总结差分约束

如果需要求的是两个变量差的最大值，那么需要将所有不等式转变成\(<=\)的形式，建图后求最短路；
如果需要求的是两个变量差的最小值，那么需要将所有不等式转化成\(>=\)的形式，建图后求最长路。

这是两个最基本的规则（算是吧）。差分约束的精髓就在于建图，而这玩意儿个人感觉没什么好办法，只能靠不停做题去找到那种感觉，自己亲自推一推式子，有些题的约束条件藏得很深甚至你看不出来这道题要用查分约束做（虽然我个人目前还没敢挑战这种题...），总而言之还是多做题吧...

查分约束模板（luoguP5960）

题意

给出一组包含 \(m\) 个不等式，有 \(n\) 个未知数的形如：

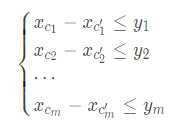
的不等式组，求任意一组满足这个不等式组的解。

简单的解释

连式子都不用自己推，根据所给的条件直接建边即可，给的式子是小于等于，所以求最大值跑最短路，看下面代码：
(洛谷里这道题是有SPJ的，所以如果答案跟样例不一样不要慌qwq，像是我这个代码样例跑出来就是0 -2 0 qwq)

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
const int maxn = 5000 + 10;
#define ll long long

struct edge{
	int nex, to, w;
}e[maxn << 2];

int head[maxn], len = 0;

void Add(int u, int v, int w){
	e[++len].to = v;
	e[len].nex = head[u];
	e[len].w = w;
	head[u] = len;
}

int n, m;
int dis[maxn], cnt[maxn];
bool vis[maxn];

int Spfa(int u){
	for(int i = 1; i <= n; i++) 
		dis[i] = 0x3f3f3f3f;
	 
	queue<int> q;
	q.push(u);
	dis[u] = 0;
	vis[u] = 1;
	while(!q.empty()){
		int x = q.front();q.pop();
		vis[x] = 0;
		for(int i = head[x]; i; i = e[i].nex){
			int v = e[i].to;
			//printf("u = %d v = %d dis[v] = %d e[i] = %d  ", x, v, dis[v], e[i].w);
			if(dis[v] > dis[x] + e[i].w){
				dis[v] = dis[x] + e[i].w;
				//printf("u = %d v = %d dis[v] = %d e[i] = %d \n", x, v, dis[v], e[i].w);
				if(!vis[v]){
					if(++cnt[v] >= n) return -1;//判负环，如果能一直跑下去说明方程无解
					vis[v] = 1;
					q.push(v);
				}
			}
		}
	}
	return 1;
}

int main(){
	cin >> n >> m;
	int u, v, w;
	for(int i = 1; i <= m; i++){
		scanf("%d %d %d", &u, &v, &w);
		Add(v, u, w); 
	}
	for(int i = 1; i <= n; i++){
		Add(0, i, 0);
	}
	if(Spfa(0) == -1) printf("NO\n");
	else for(int i = 1; i <= n; i++) printf("%d ", dis[i]);
	puts("\n");
	return 0;	
}

差分约束+模板

标签：code   ++   最长路   printf   stream   差分约束   while   put   技术   

原文地址：https://www.cnblogs.com/Zfio/p/13332349.html