标签:proc 回避 可靠 构造 准则 family mamicode 方案 pac
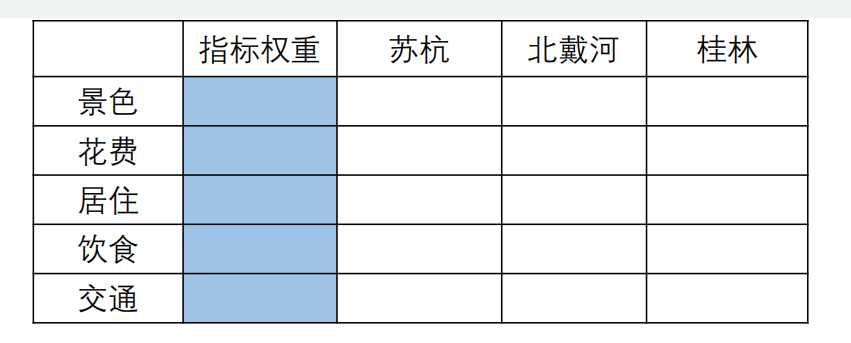
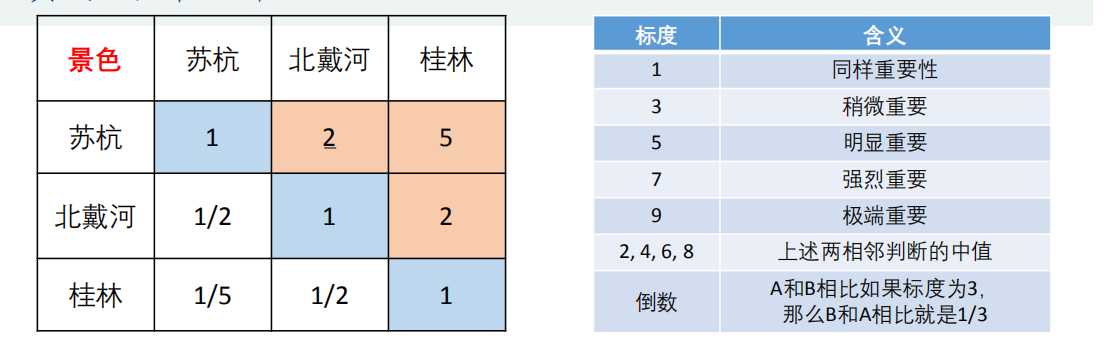
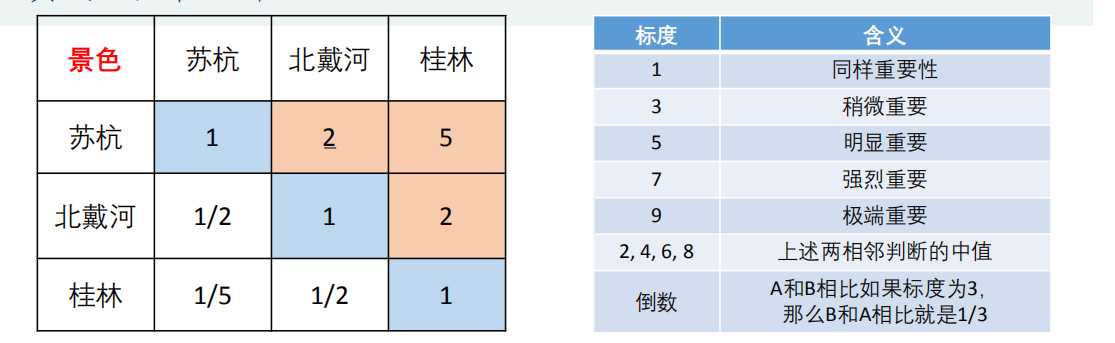
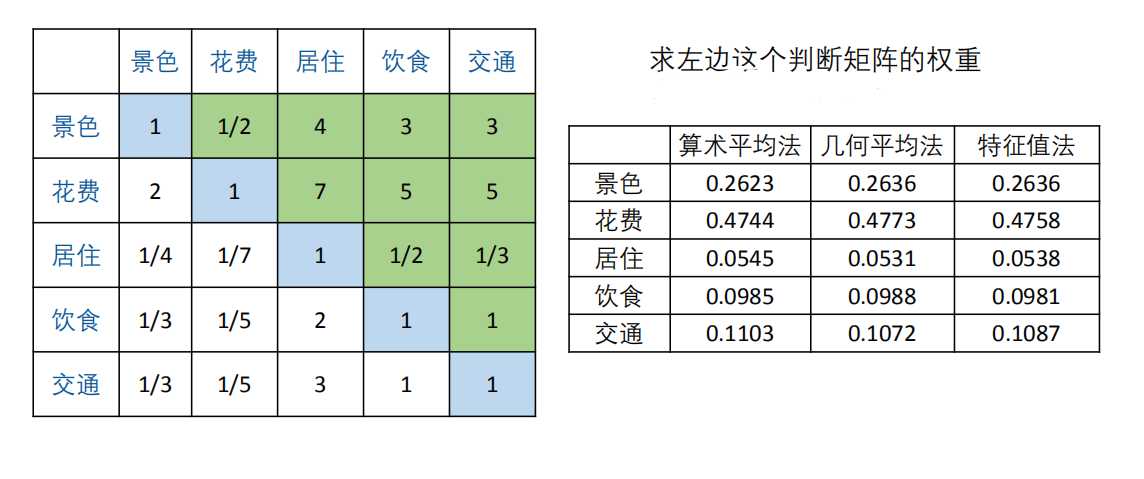
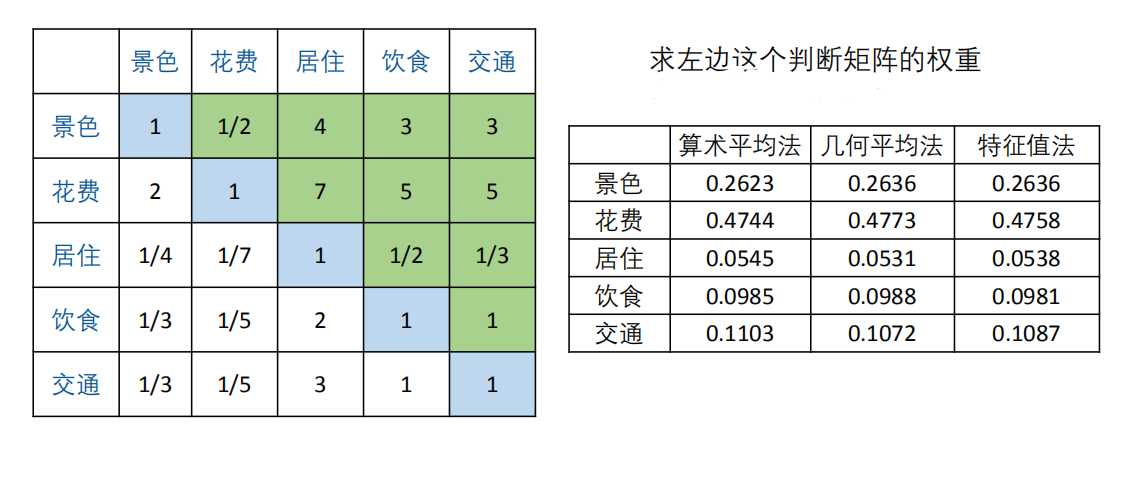
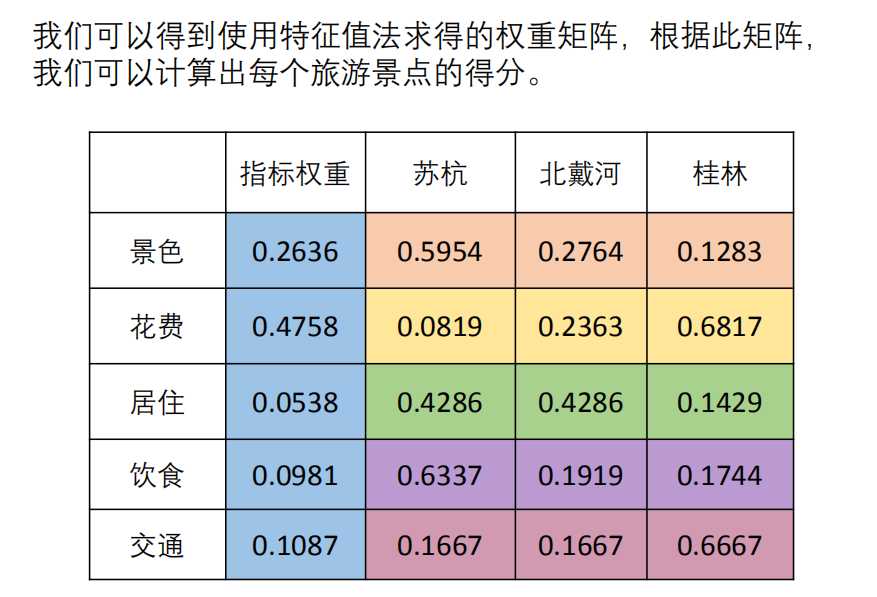
然后求出方案层对准则层的权重,汇总
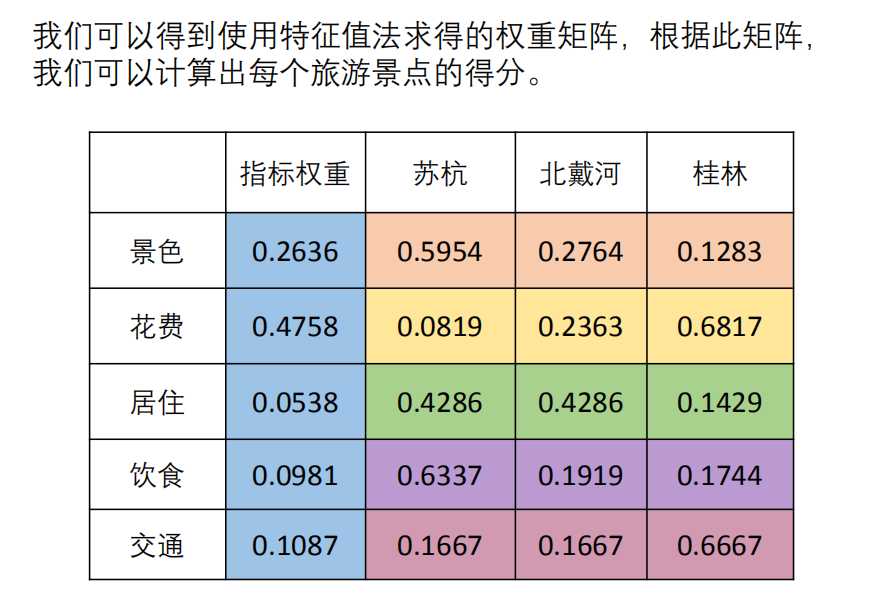
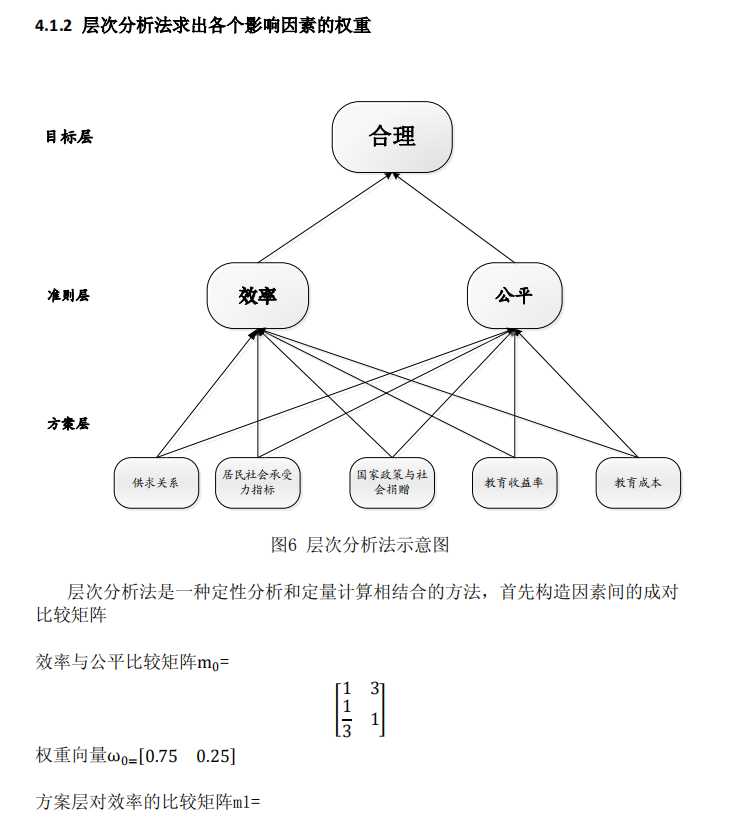
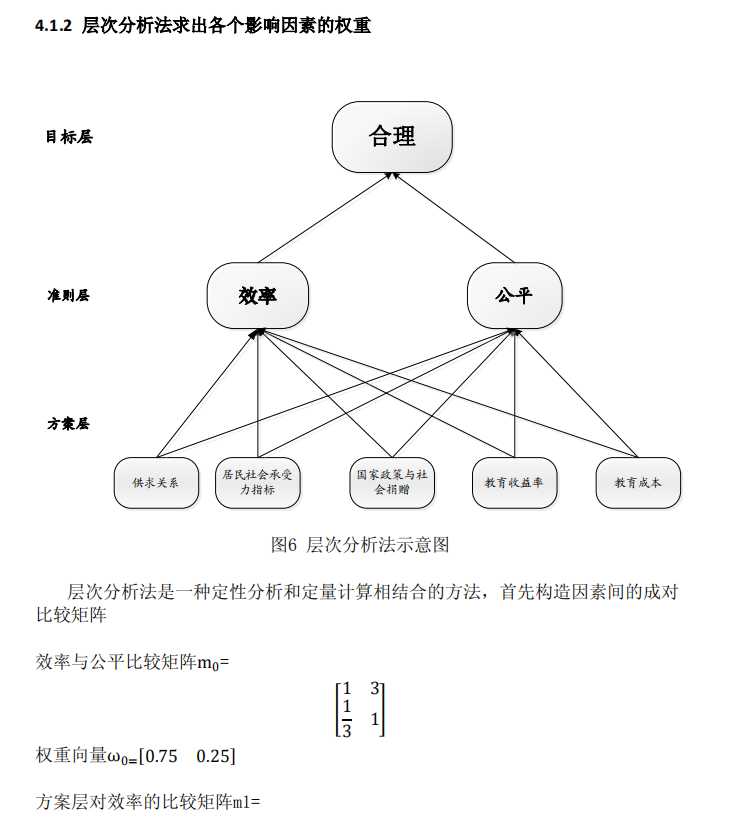

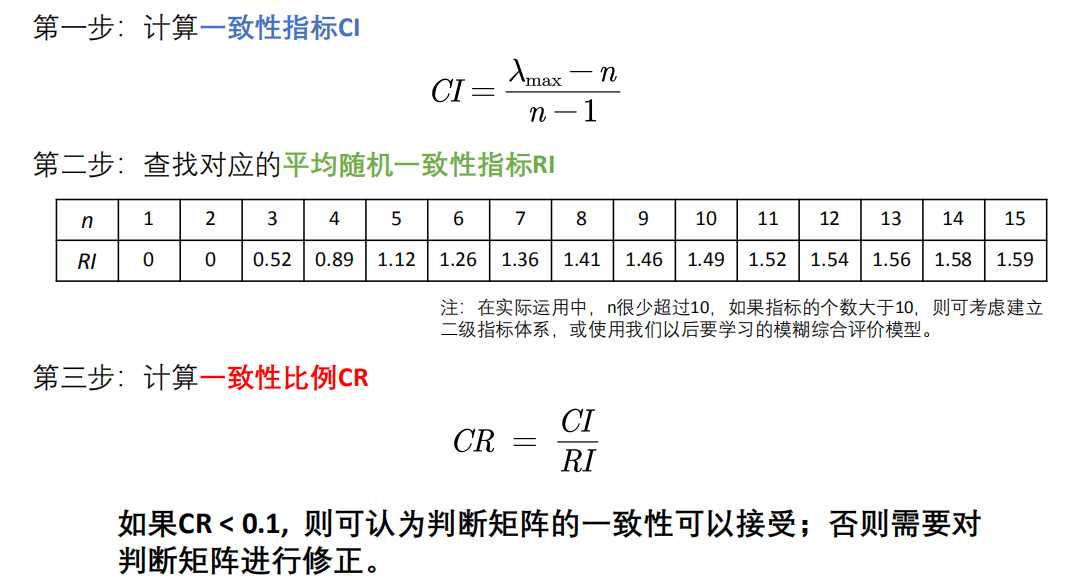
%% 注意:在论文写作中,应该先对判断矩阵进行一致性检验,然后再计算权重,因为只有判断矩阵通过了一致性检验,其权重才是有意义的。
%% 在下面的代码中,我们先计算了权重,然后再进行了一致性检验,这是为了顺应计算过程,事实上在逻辑上是说不过去的。
%% 因此大家自己写论文中如果用到了层次分析法,一定要先对判断矩阵进行一致性检验。
%% 而且要说明的是,只有非一致矩阵的判断矩阵才需要进行一致性检验。
%% 如果你的判断矩阵本身就是一个一致矩阵,那么就没有必要进行一致性检验。
disp(‘请输入判断矩阵A‘)
A=input(‘A=‘);
[n,n] = size(A);
% % % % % % % % % % % % %方法1: 算术平均法求权重% % % % % % % % % % % % %
Sum_A = sum(A);
SUM_A = repmat(Sum_A,n,1);
Stand_A = A ./ SUM_A;
disp(‘算术平均法求权重的结果为:‘);
disp(sum(Stand_A,2)./n)
% % % % % % % % % % % % %方法2: 几何平均法求权重% % % % % % % % % % % % %
Prduct_A = prod(A,2);
Prduct_n_A = Prduct_A .^ (1/n);
disp(‘几何平均法求权重的结果为:‘);
disp(Prduct_n_A ./ sum(Prduct_n_A))
% % % % % % % % % % % % %方法3: 特征值法求权重% % % % % % % % % % % % %
[V,D] = eig(A);
Max_eig = max(max(D));
[r,c]=find(D == Max_eig , 1);
disp(‘特征值法求权重的结果为:‘);
disp( V(:,c) ./ sum(V(:,c)) )
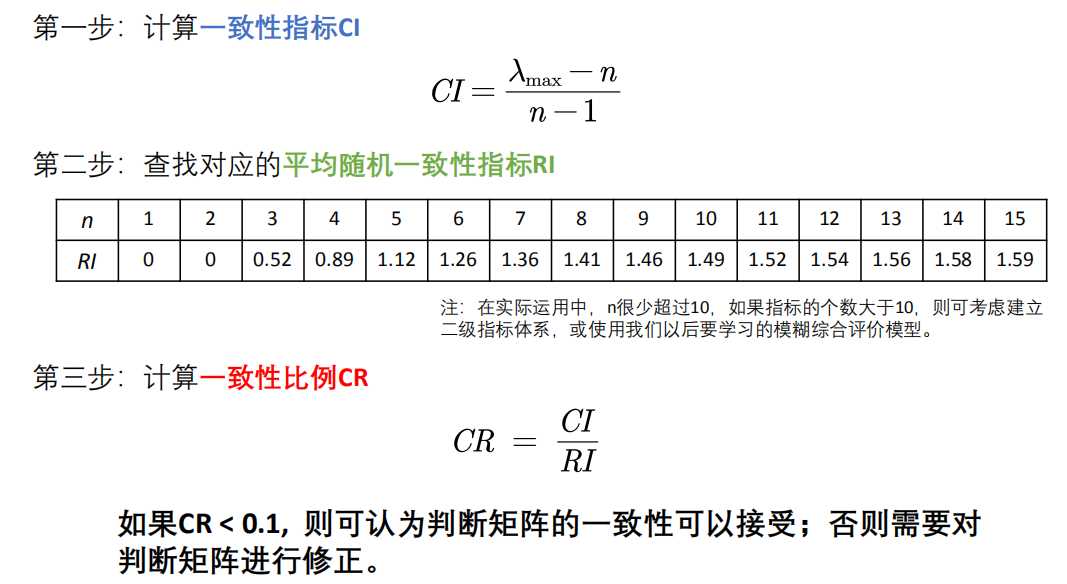
% % % % % % % % % % % % %下面是计算一致性比例CR的环节% % % % % % % % % % % % %
CI = (Max_eig - n) / (n-1);
RI=[0 0.0001 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59]; %注意哦,这里的RI最多支持 n = 15
% 这里n=2时,一定是一致矩阵,所以CI = 0,我们为了避免分母为0,将这里的第二个元素改为了很接近0的正数
CR=CI/RI(n);
disp(‘一致性指标CI=‘);disp(CI);
disp(‘一致性比例CR=‘);disp(CR);
if CR<0.10
disp(‘因为CR<0.10,所以该判断矩阵A的一致性可以接受!‘);
else
disp(‘注意:CR >= 0.10,因此该判断矩阵A需要进行修改!‘);
end
% % 注意:代码文件仅供参考,一定不要直接用于自己的数模论文中
% % 国赛对于论文的查重要求非常严格,代码雷同也算作抄袭
标签:proc 回避 可靠 构造 准则 family mamicode 方案 pac
原文地址:https://www.cnblogs.com/DWVictor/p/13335166.html