标签:info lse tar 最近公共祖先 load turn 超过 swap 根据



8 3 6
1 2
1 1
3 2
4 2
5 1
6 1
6 2
4 1
3 3
2 4
4 2
2 5
8 2
1
0
2
2
3
4
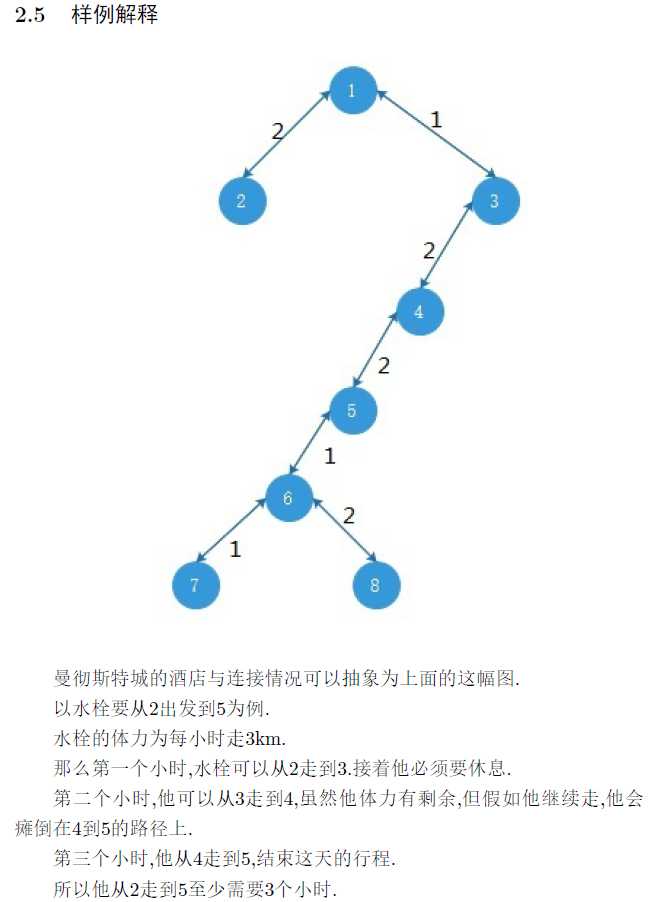
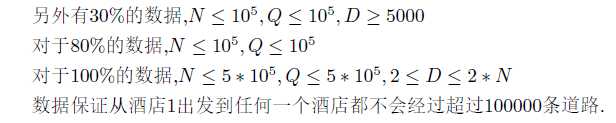
大致理一会题意,发现就是两个点 \(u,v\) 每步向上跳 \(d\) 距离,每步不能落在边上,在他们的 \(lca\) 处转身,经过 \(lca\) 直到相遇,求最少步数
而有了这句话,我们就可以直接模拟 \(u,v\) 同时一步一步往上跳,跳到离 \(lca\) 最近的点(不超过 \(lca\)),再看这两个点的距离,计算贡献
然而太慢,我们发现一步一步向上跳太 \(naive\)
又想到倍增就是改一步一步向上跳为一次向上跳 \(2^i\)步,预处理向上跳 \(2^i\) 步是谁
那么我们似乎可以同理维护一步跳距离为 \(d\),每步不能落在边上,一次跳 \(2^i\) 步是谁
记为 \(top[u][i]\),表示 \(u\) 向上跳 \(2^i\)步落在哪个点,只用算 \(top[u][0]\) 就可以得到其它的 \(top\)了。
这样忒慢的一步一步跳变成了 \(O(logn)\) 级别的
那么怎么算 \(top[u][0]\)?
我们如果从 \(u\) 处向上一条边一条边地算,那么时间是不可接受的
注意到,\(u\) 的 \(top[u][0]\) 必然是他的祖先,并且 \(top[u][0]\) 必然是 \(top[fa[u]][0]\) 或往下
那么我们就可以从 \(top[fa[u][0]]\) 处扫,不合法就往下
你向上跳的路径是固定的(你只有一个father),可往下就不一定了
所以我们开一个栈 \(stack\),\(dfs\) 到当前点 \(u\),将它入栈,那么你求 \(top[fa[u]][0]\) 往下跳时,必然是 \(top[fa[u]][0]\) 在栈中的编号加一(根据 \(dfs\) 遍历的顺序可得)
为了方便处理,我们让 \(top[u][0]\) 先表示 \(top[u][0]\) 在栈中的编号
然后回溯时让 \(top[u][0] = stack[top[u][0]]\),即变为具体的点
详细细节见 \(Code1\)
倍增,\(nlogn\),\(80\) 分
#include<cstdio>
#include<iostream>
using namespace std;
const int N = 5e5 + 5;
int n , d , q , fa[N] , anc[N][25] , f[N][25];
int tot , dep[N] , h[N] , dis[N] , st[N] , top;
struct edge{
int nxt , to;
}e[2 * N];
inline void add(int x , int y)
{
e[++tot].to = y;
e[tot].nxt = h[x];
h[x] = tot;
}
inline void dfs(int x)
{
st[++top] = x;
anc[x][0] = max(1 , anc[fa[x]][0]); //最近跳到根1,anc即上文提及的top,先存栈中的编号
while (dis[x] - dis[st[anc[x][0]]] > d) anc[x][0]++; //跳不了那么远,换栈中下一个
for(register int i = 1; i <= 21; i++)
if (f[x][i - 1]) f[x][i] = f[f[x][i - 1]][i - 1];
else break;
for(register int i = h[x]; i; i = e[i].nxt)
{
int v = e[i].to;
dep[v] = dep[x] + 1 , f[v][0] = x;
dfs(v);
}
anc[x][0] = st[anc[x][0]]; //回溯变具体的点
--top;
}
inline int LCA(int x , int y)
{
if (dep[x] < dep[y]) swap(x , y);
int deep = dep[x] - dep[y];
for(register int i = 0; i <= 21; i++)
if (deep & (1 << i)) x = f[x][i];
if (x == y) return x;
for(register int i = 21; i >= 0; i--)
if (f[x][i] != f[y][i]) x = f[x][i] , y = f[y][i];
return f[x][0];
}
inline int getans(int x , int y)
{
int lca = LCA(x , y) , res = 0;
//根据求出来的anc,让u,v同时往上跳
for(register int i = 21; i >= 0; i--)
if (dis[anc[x][i]] > dis[lca]) x = anc[x][i] , res = res + (1 << i);
for(register int i = 21; i >= 0; i--)
if (dis[anc[y][i]] > dis[lca]) y = anc[y][i] , res = res + (1 << i);
if (x == y) return res;
//处理转弯处需要的步数
if (dis[x] + dis[y] - 2 * dis[lca] <= d) return res + 1;
else return res + 2;
}
int main()
{
freopen("mancity.in" , "r" , stdin);
freopen("mancity.out" , "w" , stdout);
scanf("%d%d%d" , &n , &d , &q);
for(register int i = 2; i <= n; i++)
{
scanf("%d%d" , &fa[i] , &dis[i]);
dis[i] += dis[fa[i]];
add(fa[i] , i);
}
dfs(1);
for(register int i = 1; i <= n; i++)
for(register int j = 1; j <= 21; j++)
if (anc[i][j - 1]) anc[i][j] = anc[anc[i][j - 1]][j - 1];
else break;
int x , y;
for(register int i = 1; i <= q; i++)
{
scanf("%d%d" , &x , &y);
printf("%d\n" , getans(x , y));
}
}
正如你所见 \(O(nlogn)\) 竟然过不了
出题人毒瘤卡 \(O(nlogn)\) !
那我还要更快?!
可求 \(lca\),树剖和倍增都是 \(nlogn\) 的呀???
咦,题目似乎可以离线!
嗯,那就上 \(Tarjan\) 求 \(lca\) 吧!
\(Tarjan\) 求 \(lca\) 大致思想是将询问挂在节点上,遍历到它的时候就去处理询问
按照 \(dfs\) 遍历的顺序,我们在遍历完一个节点后将它合并的它的祖先节点
如果当前点为 \(u\) ,它的询问对象 \(v\) 已经被访问过,那么他们的最近公共祖先就是 \(find(v)\)
当然,不明白的话就去查查百度
注意,如果 \(u,v\) 是祖孙关系,那么处理询问时它们两个都会算
所以存储时要开两倍数组
不过,上面的 \(Tarjan\) 求 \(lca\) 快很多了,可计算答案怎么搞?
重新记 \(top[u]\) 表示原先的 \(top[u][0]\)
其实,我们注意到 \(u\) 所对应的 \(top[u]\) 是唯一的,它们不会形成环
于是所有的 \(top\) 关系又组成了一棵树
那么求 \(u,v\) 最接近公共祖先的两个节点时也可以同 \(Tarjan\) 一样使用并查集
我们在遍历完一个节点后将它合并的 \(top\) 节点
将询问挂在 \(lca\) 处
因为正在处理 \(lca\) ,所以查询 \(u,v\) 两点各自的 \(top\) 树的祖先绝对不会超过 \(lca\)(\(lca\) 还没合并到它的 \(top\))
所以我们直接 \(find(u),find(v)\),就得到了离 \(lca\) 最近的点。当然,求步数时给并查集加个权值就好了
然后转弯时上文同理
详见 \(Code2\)
\(Tarjan\) , 并查集, \(O(n \alpha(n))\),\(100\) 分
#include<cstdio>
#include<iostream>
using namespace std;
const int N = 5e5 + 5;
int n , d , q , top[N] , stop , stack[N];
int tot1 , tot2 , tot3 , tot4 , h1[N] , h2[N] , h3[N] , h4[N];
int dis[N] , fa[N] , vis[N] , ask[N][3] , ans[N] , dist[N];
struct edge{
int nxt , to;
}e1[N] , e2[N] , e4[2 * N];
struct edgeask{
int nxt , to , id;
}e3[2 * N];
inline void add1(int x , int y) //原来的树
{
e1[++tot1].to = y;
e1[tot1].nxt = h1[x];
h1[x] = tot1;
}
inline void add2(int x , int y) //Top关系树
{
e2[++tot2].to = y;
e2[tot2].nxt = h2[x];
h2[x] = tot2;
}
inline void add3(int x , int y , int z) //ask,Tarjan时用来求一个点和其询问对象的 $lca$
{
e3[++tot3].to = y;
e3[tot3].id = z;
e3[tot3].nxt = h3[x];
h3[x] = tot3;
}
inline void add4(int x , int y) //lca处处理询问,即在询问挂在lca处,遍历到时再处理
{
e4[++tot4].to = y;
e4[tot4].nxt = h4[x];
h4[x] = tot4;
}
inline int find1(int x) //tarjan时所用的并查集的find
{
if (fa[x] == x) return x;
fa[x] = find1(fa[x]);
return fa[x];
}
inline int find2(int x) //top关系树所用的并查集的find
{
if (top[x] == x) return x;
int t = top[x];
top[x] = find2(top[x]);
dist[x] += dist[t]; //路压合并时,加上它father的权值
return top[x];
}
inline void dfs1(int u)
{
//同理计算top
stack[++stop] = u;
top[u] = max(1 , top[fa[u]]);
while (dis[u] - dis[stack[top[u]]] > d) top[u]++;
for(register int i = h1[u]; i; i = e1[i].nxt)
dfs1(e1[i].to);
top[u] = stack[top[u]]; //更换为具体点
--stop;
add2(top[u] , u);
}
inline void dfs2(int u)
{
top[u] = u , fa[u] = u , vis[u] = 1;
for(register int i = h1[u]; i; i = e1[i].nxt)
{
dfs2(e1[i].to);
fa[e1[i].to] = u;
}
for(register int i = h3[u]; i; i = e3[i].nxt) //求lca
{
int v = e3[i].to;
if (!vis[v]) continue;
add4(find1(v) , e3[i].id);
}
for(register int i = h4[u]; i; i = e4[i].nxt) //lca处处理询问
{
int id = e4[i].to , x = ask[id][0] , y = ask[id][1];
int xx = x , yy = y;
x = find2(x) , y = find2(y); //求两个浅点
int m = dis[x] + dis[y] - dis[u] * 2;
ans[id] = dist[xx] + dist[yy] + (m > 0) + (m > d);
}
for(register int i = h2[u]; i; i = e2[i].nxt) top[e2[i].to] = u , dist[e2[i].to] = 1; //维护top
}
int main()
{
freopen("mancity.in" , "r" , stdin);
freopen("mancity.out" , "w" , stdout);
scanf("%d%d%d" , &n , &d , &q);
for(register int i = 2; i <= n; i++)
{
scanf("%d%d" , &fa[i] , &dis[i]);
dis[i] += dis[fa[i]];
add1(fa[i] , i);
}
dfs1(1);
for(register int i = 1; i <= q; i++)
{
scanf("%d%d" , &ask[i][0] , &ask[i][1]);
add3(ask[i][0] , ask[i][1] , i) , add3(ask[i][1] , ask[i][0] , i); //将询问挂上去
}
dfs2(1);
for(register int i = 1; i <= q; i++) printf("%d\n" , ans[i]);
}
标签:info lse tar 最近公共祖先 load turn 超过 swap 根据
原文地址:https://www.cnblogs.com/leiyuanze/p/13339362.html