标签:存在 一半 lin nlog 运用 name aik cos 变换
快速傅里叶变换(fast Fourier transform),即利用计算机计算离散傅里叶变换(DFT)的高效、快速计算方法的统称,简称FFT。快速傅里叶变换是1965年由J.W.库利和T.W.图基提出的。采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少。
对于一个多项式\(A(x)\),其系数表示法可表示为
\(A(x)=\sum_{i=0}^n{a_i*x^i}={a_0}+{a_1*x}+{a_2*x^2}+...+{a_n*x^n}\)
在系数表示法下,两个多项式相乘的乘法规则为其中一个多项式的每一项与另一个多项式每一项相乘后相加
故该种方式求多项式乘法的时间复杂度为\(O(n^2)\)
将互不相同的 \(x_i\) 代入多项式中会得到互不相同的 \(y_i\)
获得的这些点也就是多项式函数图像上的点坐标 \((x_i,y_i)\)
可以证明,多项式可以由这些点唯一确定
获得这些点后,只需要在两个多项式对应的点值位置进行一次数值乘法即可获得相乘后得到的多项式对应位置的值
\(y_i\) 的值满足 \(y_i=\sum_{j=0}^na_j*x_i^j\)
若仅至此,即使是点值表示法计算多项式乘法时间复杂度也是\(O(n^2)\)的,但在这部分可以进行优化
定义虚数单位\(i^2=-1\),令\(a\)、\(b\)为两实数,形如\(a+bi\)的数即为复数
FFT 要求\(n\)必须为\(2\)的正整数次幂
首先对于选点,点值表示法选点并不是随意的,而是选择复平面上具有特殊性质的\(n\)个点作为待代入的点
将复平面上以原点为圆心,\(1\)为半径的圆\(n\)等分,作从原点出发终点为这些点的\(n\)个向量,设正幅度角(实数轴正方向逆时针旋转得到的夹角)最小的向量为单位根\(w_n\),记作\(n\)次单位根
故这\(n\)个向量可表示为 \(w_n^1,w_n^2,w_n^3...w_n^n\),且\(w_n^n=w_n^0\)
这些向量值可以利用欧拉公式 \(w_n^k=\frac{2\pi}{n}cos\ k+\frac{2\pi}{n}i\ sin\ k\) 获得
设多项式\(A(x)\)的系数为\((a_0,a_1,a_2...a_{n-1})\)
则多项式可表示为\(A(x)=a_0+a_1x+a_2x^2+a_3x^3+...+a_{n-1}x^{n-1}\)
将系数奇偶分开
设\(A_1(x^2)=a_1+a_3x+a_5x^2+...+a_{n-1}x^{\frac{n}{2}-1}\)
\(A_2(x^2)=a_0+a_2x+a_4x^2+...+a_{n-2}x^{\frac{n}{2}-1}\)
可得\(A(x)=xA_1(x^2)+A_2(x^2)\)
将\(x=w_n^k(k<\frac{n}{2})\)代入得\(A(w_n^k)=w_n^kA_1(w_n^{2k})+A_2(w_n^{2k})=w_n^kA_1(w_{\frac{n}{2}}^k)+A_2(w_{\frac{n}{2}}^k)\)
将\(x=w_n^{k+\frac{n}{2}}(k<\frac{n}{2})\)代入得\(A(w_n^{k+\frac{n}{2}})=w_n^{k+\frac{n}{2}}A_1(w_n^{2({k+\frac{n}{2}})})+A_2(w_n^{2({k+\frac{n}{2}})})=A_2(w_n^{2k})-w_n^kA_1(w_n^{2k})\)
至此,可以发现两式仅有一常数项不同,故在求第一个式子时也能直接将第二个式子求出
故此时待计算的部分缩小了一半
可知缩小后的式子仍然满足上述性质,故该部分可由迭代来在\(O(logn)\)的时间内求出
基于此性质,快速傅里叶变换的总时间复杂度为\(O(nlogn)\)
主要部分实现方法图示(图是网上的,来自远航之曲大佬):
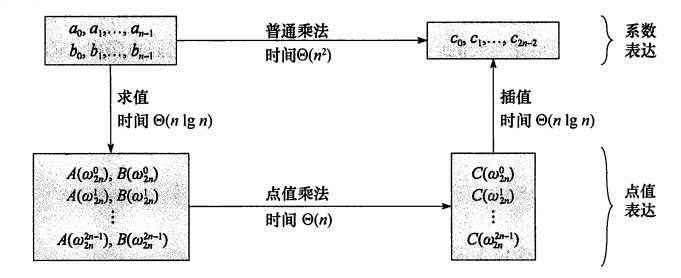
对于快速傅里叶逆变换,本文不作阐述(推公式太麻烦),记用法即可
首先对于复数,需要定义一个complex类来装载
C++的STL中已经存在complex以供使用,但建议还是手动定义
struct cp
{
double x,y;
cp(double u=0,double v=0){x=u,y=v;}
friend cp operator +(const cp &u,const cp &v){return cp(u.x+v.x,u.y+v.y);}
friend cp operator -(const cp &u,const cp &v){return cp(u.x-v.x,u.y-v.y);}
friend cp operator *(const cp &u,const cp &v){return cp(u.x*v.x-u.y*v.y,u.x*v.y+u.y*v.x);}
};
首先根据需求范围\(n\)求出进行FFT操作的上界\(lim\) (需为\(2\)的正整数次幂)
int lim=1;
void initFFT(int n)
{
int lg=0;
while(lim<=n)
lg++,lim<<=1;
}
※ 对于FFT的位置,还能在位置交换上通过预处理来进一步提升效率(蝴蝶迭代)
const int N=200050;
int rev[N],lim=1;
void initFFT(int n)
{
int lg=0;
while(lim<=n)
lg++,lim<<=1;
for(int i=0;i<lim;i++)
rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1)); //由于i可以看做是i/2二进制上的每一位左移一位得来,所以逆变换可以视为右移一位,同时处理下奇数
}
调用initFFT以获得上界\(lim\)后,即可开始进行快速傅里叶变换(板子不是使用迭代法的)
void FFT(cp *a,int opr) //a为待进行FFT的复数数组,opr为1即FFT,opr为-1即IFFT(快速傅里叶逆变换)
{
for(int i=0;i<lim;i++)
if(i<rev[i])
swap(a[i],a[rev[i]]); //借助蝴蝶迭代预处理得到的数组以快速交换
for(int md=1;md<lim;md<<=1)
{
cp rt=cp(cos(PI/md),opr*sin(PI/md)); //以欧拉公式快速获得root
for(int stp=md<<1,pos=0;pos<lim;pos+=stp)
{
cp w=cp(1,0);
for(int i=0;i<md;i++,w=w*rt)
{
cp x=a[pos+i],y=w*a[pos+md+i];
a[pos+i]=x+y;
a[pos+md+i]=x-y;
}
}
}
}
const int N=200050;
int lim=1,rev[N];
struct cp
{
double x,y;
cp(double u=0,double v=0){x=u,y=v;}
friend cp operator +(const cp &u,const cp &v){return cp(u.x+v.x,u.y+v.y);}
friend cp operator -(const cp &u,const cp &v){return cp(u.x-v.x,u.y-v.y);}
friend cp operator *(const cp &u,const cp &v){return cp(u.x*v.x-u.y*v.y,u.x*v.y+u.y*v.x);}
}f[N],g[N];
void FFT(cp *a,int opr)
{
for(int i=0;i<lim;i++)
if(i<rev[i])
swap(a[i],a[rev[i]]);
for(int md=1;md<lim;md<<=1)
{
cp rt=cp(cos(PI/md),opr*sin(PI/md));
for(int stp=md<<1,pos=0;pos<lim;pos+=stp)
{
cp w=cp(1,0);
for(int i=0;i<md;i++,w=w*rt)
{
cp x=a[pos+i],y=w*a[pos+md+i];
a[pos+i]=x+y;
a[pos+md+i]=x-y;
}
}
}
}
void initFFT(int n)
{
int lg=0;
while(lim<=n)
lg++,lim<<=1;
for(int i=0;i<lim;i++)
rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1));
}
单纯的模板题,问的即为两多项式的卷积(即多项式相乘后得到的新多项式)
解法:
将两个多项式进行FFT,变换成点值表示法后直接在对应位置相乘,最后进行IFFT即可
#include<bits/stdc++.h>
using namespace std;
const int N=5000050;
const double PI=acos(-1.0);
int lim=1,rev[N];
struct cp
{
double x,y;
cp(double u=0,double v=0){x=u,y=v;}
friend cp operator +(const cp &u,const cp &v){return cp(u.x+v.x,u.y+v.y);}
friend cp operator -(const cp &u,const cp &v){return cp(u.x-v.x,u.y-v.y);}
friend cp operator *(const cp &u,const cp &v){return cp(u.x*v.x-u.y*v.y,u.x*v.y+u.y*v.x);}
}f[N],g[N];
void FFT(cp *a,int tp)
{
for(int i=0;i<lim;i++)
if(i<rev[i])
swap(a[i],a[rev[i]]);
for(int md=1;md<lim;md<<=1)
{
cp rt=cp(cos(PI/md),tp*sin(PI/md));
for(int stp=md<<1,pos=0;pos<lim;pos+=stp)
{
cp w=cp(1,0);
for(int i=0;i<md;i++,w=w*rt)
{
cp x=a[pos+i],y=w*a[pos+md+i];
a[pos+i]=x+y;
a[pos+md+i]=x-y;
}
}
}
}
void initFFT(int n)
{
int lg=0;
while(lim<=n)
lg++,lim<<=1;
for(int i=0;i<lim;i++)
rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1));
}
int main()
{
int n,m;
scanf("%d%d",&n,&m);
initFFT(n+m);
for(int i=0;i<=n;i++)
cin>>f[i].x; //存在复数的实部中
for(int i=0;i<=m;i++)
cin>>g[i].x;
FFT(f,1);
FFT(g,1);
for(int i=0;i<=lim;i++)
f[i]=f[i]*g[i]; //直接计算卷积
FFT(f,-1); //逆变换
for(int i=0;i<=n+m;i++)
printf("%d ",(int)round(f[i].x/lim)); //逆变换后需要除以lim,注意四舍五入(精度问题)
return 0;
}
P1919 【模板】A*B Problem升级版(FFT快速傅里叶)
解法:
FFT的处理部分与上题类似
注意到一个十进制数字可以看作是一个\(x=10\)的多项式
例如\(123=1*10^2+2*10+3\)
所以两个数字的乘法即为两个\(x=10\)的多项式相乘
注意最后逆变换后可能会导致某个位置的系数\(≥10\),所以注意进位处理即可
#include<bits/stdc++.h>
using namespace std;
const int N=4000050;
const double PI=acos(-1.0);
int lim=1,rev[N];
struct cp
{
double x,y;
cp(double u=0,double v=0){x=u,y=v;}
friend cp operator +(const cp &u,const cp &v){return cp(u.x+v.x,u.y+v.y);}
friend cp operator -(const cp &u,const cp &v){return cp(u.x-v.x,u.y-v.y);}
friend cp operator *(const cp &u,const cp &v){return cp(u.x*v.x-u.y*v.y,u.x*v.y+u.y*v.x);}
}f[N],g[N];
void FFT(cp *a,int tp)
{
for(int i=0;i<lim;i++)
if(i<rev[i])
swap(a[i],a[rev[i]]);
for(int md=1;md<lim;md<<=1)
{
cp rt=cp(cos(PI/md),tp*sin(PI/md));
for(int stp=md<<1,pos=0;pos<lim;pos+=stp)
{
cp w=cp(1,0);
for(int i=0;i<md;i++,w=w*rt)
{
cp x=a[pos+i],y=w*a[pos+md+i];
a[pos+i]=x+y;
a[pos+md+i]=x-y;
}
}
}
}
void initFFT(int n)
{
int lg=0;
while(lim<=n)
lg++,lim<<=1;
for(int i=0;i<lim;i++)
rev[i]=(rev[i>>1]>>1)|((i&1)<<(lg-1));
}
char s1[N],s2[N];
int ans[N];
int main()
{
scanf("%s%s",s1,s2);
initFFT(strlen(s1)+strlen(s2));
for(int i=strlen(s1)-1,j=0;i>=0;i--,j++) //倒序存入,十进制数字次数最低的位在最后
f[j].x=s1[i]-‘0‘;
for(int i=strlen(s2)-1,j=0;i>=0;i--,j++)
g[j].x=s2[i]-‘0‘;
FFT(f,1);
FFT(g,1);
for(int i=0;i<=lim;i++)
f[i]=f[i]*g[i];
FFT(f,-1);
int tmp=0;
for(int i=0;i<=lim;i++)
{
ans[i]+=(int)(f[i].x/lim+0.5);
if(ans[i]>=10)
{
ans[i+1]+=ans[i]/10;
ans[i]%=10;
if(i==lim)
lim++;
}
}
while(ans[lim]==0&&lim>=1)
lim--;
while(lim>=0)
{
printf("%d",ans[lim]);
lim--;
}
putchar(‘\n‘);
return 0;
}
标签:存在 一半 lin nlog 运用 name aik cos 变换
原文地址:https://www.cnblogs.com/stelayuri/p/13347896.html