标签:利用 html ike loading img one 空间 sdn 形式
这次我们来拟合一个椭球,之前也拟合过空间的椭圆,不过当时只用了五个点,方程组应该是欠定的,看看就好。
要拟合椭球,首先设定椭球一般方程:
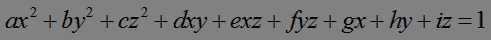
根据这个方程和已有的空间椭球点数据,利用最小二乘就能得到上面九个参数。
不过有时候我们想要的不是这样的一般方程,而是椭球的球心和三个半长轴。
下面就来说明如何根据椭球一般方程求取球心和半长轴。
首先把上述方程写成矩阵形式:
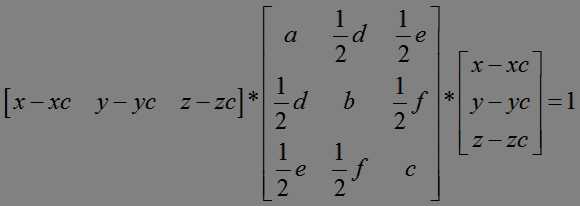
其中xc,yc,zc为球心。
对上式进行展开,得到:
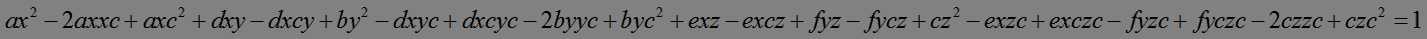
上式和第一个式子相比,求对应一次项相等时的结果。
可以用Mathematica来求:
A = {x - xc, y - yc, z - zc};
B = {{a, 1/2*d, 1/2*e}, {1/2*d, b, 1/2*f}, {1/2*e, 1/2*f, c}};
Factor[Dot[A, B, Transpose[{A}]]]
{a x^2 - 2 a x xc + a xc^2 + d x y - d xc y + b y^2 - d x yc +
d xc yc - 2 b y yc + b yc^2 + e x z - e xc z + f y z - f yc z +
c z^2 - e x zc + e xc zc - f y zc + f yc zc - 2 c z zc + c zc^2}
CoefficientList[Factor[Dot[A, B, Transpose[{A}]]], {x, y, z}]
{{{{a xc^2 + d xc yc + b yc^2 + e xc zc + f yc zc + c zc^2, -e xc -
f yc - 2 c zc, c}, {-d xc - 2 b yc - f zc, f, 0}, {b, 0,
0}}, {{-2 a xc - d yc - e zc, e, 0}, {d, 0, 0}, {0, 0, 0}}, {{a,
0, 0}, {0, 0, 0}, {0, 0, 0}}}}
得到下面这样的方程组:
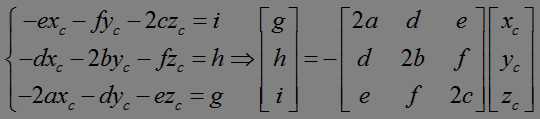
即可求出Xc,Yc,Zc。
半长轴的计算可以参考这里:https://www.zhihu.com/question/47033644/answer/112864757
椭球拟合代码如下:
clear all; close all; clc; xc = 1.21; yc = 2.32; zc = 4.32; xr = 2.78; yr = 5.76; zr = 1.51; [x,y,z] = ellipsoid(xc,yc,zc,xr,yr,zr,20); plot3(x(:),y(:),z(:),‘.‘); x=x(:); y=y(:); z=z(:); X = [x.*x y.*y z.*z x.*y x.*z y.*z x y z]; Y = ones(length(x),1); C = inv(X‘*X)*X‘*Y; M=[C(1) C(4)/2 C(5)/2; C(4)/2 C(2) C(6)/2; C(5)/2 C(6)/2 C(3)]; Cent = -0.5*[C(7) C(8) C(9)]*inv(M) S = Cent*M*Cent‘+1; [U,V]=eig(M); [~,indx] = max(abs(U(1,:))); [~,indy] = max(abs(U(2,:))); [~,indz] = max(abs(U(3,:))); R = [sqrt(S/V(indx,indx)) sqrt(S/V(indy,indy)) sqrt(S/V(indz,indz))]
结果和预设的值是一致的:

参考:https://blog.csdn.net/shenshikexmu/article/details/70143455
标签:利用 html ike loading img one 空间 sdn 形式
原文地址:https://www.cnblogs.com/tiandsp/p/13222319.html