有约束的非线性规划的求解

标签：线性   转化   case   http   cas   splay   变量   最大   fun   

标准形式：

调用 fmincon() 函数：

[x,favl]=fmincon(@fun,x0,A,b,Aeq,beq,vlb,vub,@con)

求解流程：

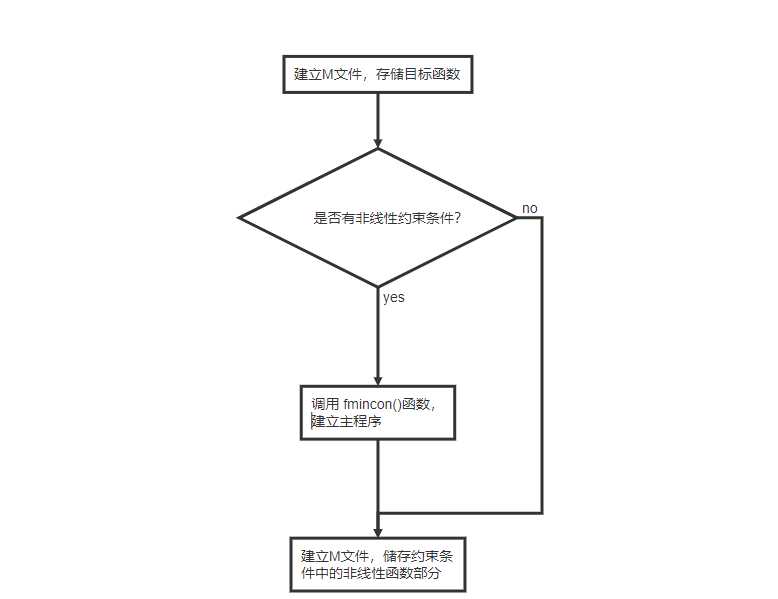
例：

转化为标准形式：

①：

function f=fun(x)
f=-x(1)^2-x(2)^2+x(1)*x(2)+2*x(1)+5*x(2);
end

②

function [G,Geq]=cont(x)
G=(x(1)-1)^2-x(2);
Geq=[];
end

③

x0=[0 1];
A=[-2,3];
b=6;
Aeq=[];
beq=[];
lb=[];
ub=[];
[x,favl]=fmincon(@fun,x0,A,b,Aeq,beq,lb,ub,@cont)

运行结果可知，最大值为-1：

x =

    1.0000    0.0000


favl =

    1.0000

>> 

有约束的非线性规划的求解

标签：线性   转化   case   http   cas   splay   变量   最大   fun   

原文地址：https://www.cnblogs.com/Noturns/p/13350518.html