标签：cin http 并且 展开 产生 细节 影响 表示 模型
FM的论文名字为《Factorization Machines》，其核心思想是组合一阶和二阶特征，基于K维的隐向量，处理因为数据稀疏带来的学习不足问题。并且通过公式推导出其学习时间是线性的，非常适用于大规模的推荐系统。首先从LR到多项式模型方程再到FM进行演进的梳理，随后对于论文中的某些细节进行展开。
演进梳理：
一、LR模型方程
回顾一般的线性回归方程LR，对于输入任意一个n维特征向量，建模估计函数
为
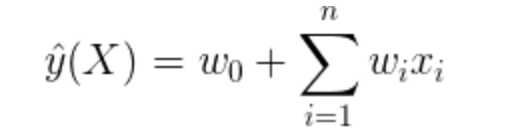
LR模型的参数为：，
从LR模型方程中我们可以看到：
（1）各个特征分量
和
彼此之间是独立的
（2）
将单个特征分量线性的组合起来，却忽略了特征分量彼此之间的相互组合关系
对于特征的组合关系，我们定义：
（1）一阶特征：即单个特征，不产生新特征，如
（2）二阶特征：即两个特征组合产生的新特征，如
（3）高阶特征：即两个以上的特征组合产生的新特征，如
所以LR模型只考虑了一阶特征的线性组合关系
二、多项式模型方程
为了克服模型欠缺二阶特征组合因素，我们将LR模型改写为二阶多项式模型
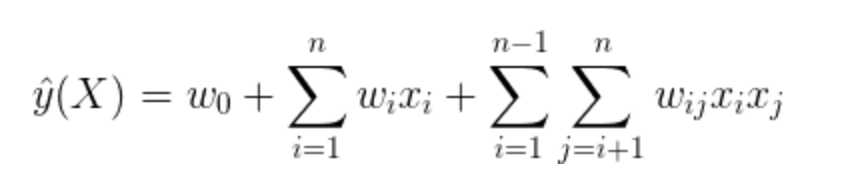
其中表示两个互异特征组合的二阶特征，
表示二阶特征的交叉项系数
至此，该模型似乎已经加入了特征组合的因素，接下来只要学习参数即可
但是，上述二阶多项式模型却有一个致命的缺陷：
数据稀疏性普遍存在的实际应用场景中，二阶特征系数
的训练是很困难的
造成学习困难的原因是：
（1）
都非零的样本
（2）样本本身是稀疏的，同时满足
的样本非常稀少
所以多项式模型虽然加入了二阶特征组合，却受到数据稀疏的影响
三、FM模型方程
为了克服模型无法在稀疏数据场景下学习二阶特征系数，我们需要将
表示为另外一种形式
为此，针对样本的第i维特征分量
，引入辅助隐向量
其中k为超参数，表示特征分量对应一个k维隐向量
，则将
表示为：
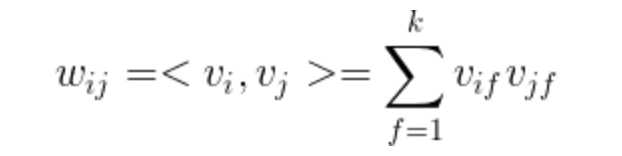
上式引入隐向量的含义为：
二阶特征系数
和
的内积
，这就是FM模型的核心思想
则我们将二阶多项式模型改写为FM模型
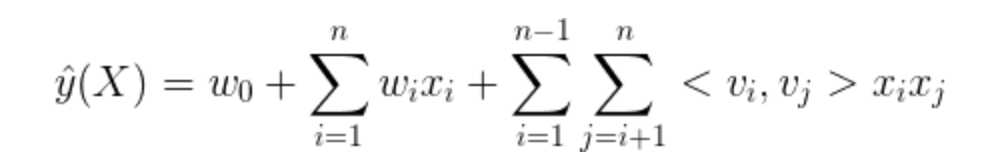
从FM模型方程可知，FM模型的参数为：
各个参数的意义为：
（1）
表示FM模型的偏置
（2）
表示FM模型对一阶特征的建模
（3）
表示FM模型对二阶特征的建模
参数的个数为：
模型的复杂度为：
公式细节：
1、关注模型中的第三项：
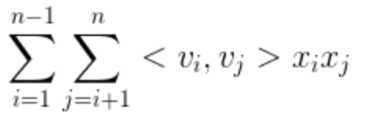
其中<v1,v2>该项的具体展开如图所示：
2、在证明该模型具有线性时间复杂度的第一步时，用到如下的方法证明：
标签：cin http 并且 展开 产生 细节 影响 表示 模型
原文地址：https://www.cnblogs.com/yuanmingzhou/p/13358056.html
