标签:因此 均值 转换 随机选择 智能 建立 步骤 测试 margin
基于未知情况的WSS失效异常数据预测判断方法
对于WSS失效异常数据的预测判断,其主要目的是针对未来可能出现的一些未知异常情况,基于对整体WSS不同维度指标数据的分析和挖掘,建立起一套可预测判断未来指标数据异常的WSS失效异常数据智能预测判断系统和集群,从而实现对未来为未知异常类型的数据进行筛选,也为后续指标异常类型的专家诊断提供数据和特征分布基础。
异常情况数据的智能预测判断,其本质是实现WSS失效异常数据判断的逆向工程,具体来说,其实就是由原来已知“病”的类型及其症状影响特征(指标特征影响规律),结合实际症状具体表现,判断“是否患“病”(即是否为失效异常数据),实现现在在未知“病”的类型及其症状影响表现的情况下,直接根据实际情况下不同指标数据分布的差异性和相似性来“筛查”出可能出现异常的数据集群,从而实现未来对WSS指标数据中未知失效异常数据的预测判断输出。
对于未来未知类型的WSS失效异常数据的预测判断,其难点主要是未来可能出现未知异常情况的多样性,复杂性,以及不同异常情况下可能对其不同特征不同维度指标数据影响的随机性,这对后续的智能预测判断模型提出了很高的泛化能力要求,需要尽可能地去匹配和适用更多未来的未知异常情况。
由于未来异常情况的未知性,多样性以及复杂性,所以想要建立起一套泛化能力较好的智能预测判断系统或者机制是有一定难度的。
基于对未来未知异常出现的可能性分析,项目采取的主要解决思路是采取不同可能异常情况分类分模型建立的方法,建立起适用于不同特点未知异常类型的不同预测判断模型,然后在后续的实验和数据积累中,不断扩展新的方法模型,并不停地修正各个模型。
目前针对未知异常与正常情况数据可能存在的分布差异类型,主要从以下两大方向进行预测判断模型的建立:
(1)针对不同时间点WSS正常情况和失效异常情况下指标特征数据分布的较大差异性,建立起特征差异性预测判断模型,其核心在于在不同时间点处未知异常数据分布的相似性,群聚性以及与正常情况下数据分布的较大差异性。
对于这种情况,主要包含两个不同类型的预测机制模型:
1)未知异常的指标数据分布与正常情况具有较大的差异(即高维特征数据分布下具有较为明显的分布边界),并且正常情况和未知异常情况数据分布具有较高的集群分布性,此时可以采取基于数据相似性集群分布的非监督学习聚类的算法模型;
2)未知异常的数据分布与正常情况下具有较大的差异,但是未知异常数据分布零散,不具备集群分布性,此时可以采取的方法是基于异常检测方法的算法模型
(2)针对一定时间周期窗口T以内的WSS正常情况和失效异常情况下指标特征数据的波形差异性,建立起波形差异性预测判断模型,其核心在于不同时间周期内未知异常数据波形变化的相似性和群聚性,以及与正常情况下数据波形分布的差异性。
这种情况以时间分析维度为主体,通过一定时间内波形的特征相似性来进行异常情况的筛选和预测判断,主要包含以下几种情况:
1)通过时域波形变化的趋势相似性来进行异常和正常情况的预测判断,其核心在于计算出时域条件下不同指标数据分布的波形相似度,最终预测判断的准确性取决于波形相似度计算的方法;
2)通过时域条件下波形的频域转换,进行频域的对比和分析,最终预测判断出未知异常的数据;
3)通过时域波形相似度分析和频域分析相结合的方法来进行未知异常情况数据的预测判断输出。
4. 具体算法模型实现:
(1)基于指标特征数据相似性集群分布的非监督学习聚类算法模型
该模型主要适用于WSS指标正常数据和未知异常数据的指标特征数据分布范围差异较大,具有明显的集群相似性,这样便可以很好地对正常情况和未知异常情况进行指标特征数据的集群聚类,同时保持一定的准确性。
模型的主体算法是基于欧氏距离进行聚类是实现的非监督学习算法K-means算法,该方法是一种经典的机器学习聚类算法。
1)算法主体思想
K-means方法是聚类中的经典算法,其主体的算法思想是以数据中随机的k个点作为中心进行欧氏距离计算与聚类,对最靠近他们的对象归类,通过不断迭代的方法,逐次更新各聚类中心的值,直到得到最好的聚类结果。
具体来说,它在数据集中根据一定策略选择K个点作为每个簇的初始中心,然后观察剩余的数据,将数据划分到距离这K个点最近的簇中,也就是说将数据划分成K个簇完成一次划分,但形成的新簇并不一定是最好的划分,因此生成的新簇中,重新计算每个簇的中心点,然后在重新进行划分,直到每次划分的结果保持不变。在实际应用中往往经过很多次迭代仍然达不到每次划分结果保持不变,甚至因为数据的关系,根本就达不到这个终止条件,实际应用中往往采用变通的方法设置一个最大迭代次数,当达到最大迭代次数时,终止计算。具体的原理如下图所示:
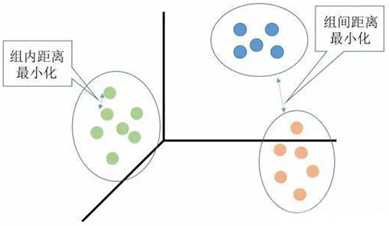
图 基于欧式距离的相似性聚类算法原理图
2)算法的具体步骤:
① 随机选择K个中心点
② 把每个数据点分配到离它最近的中心点;
③ 重新计算每类中的点到该类中心点距离的平均值;
④ 分配每个数据到它最近的中心点;
⑤ 重复步骤3和4,直到所有的观测值不再被分配或是达到最大的迭代次数(算法本身可以设置最大的迭代次数)。
具体的步骤可如下图所示:
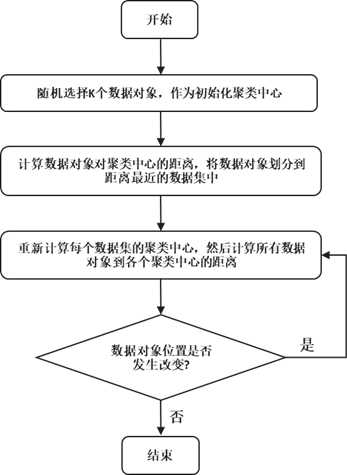
图 k-means非监督聚类算法基本实现步骤
3)算法在异常检测预测判断的仿真尝试(以二维数据进行展示分析):
①直接采用k-means算法进行异常数据点的聚类
直接采用k-means聚类分析进行WSS数据的聚类和尝试,其结果中会因为正常数据和异常数据的分布数量的相对比例而出现分类结果的不同情况,其测试的分类结果展示如下图所示:
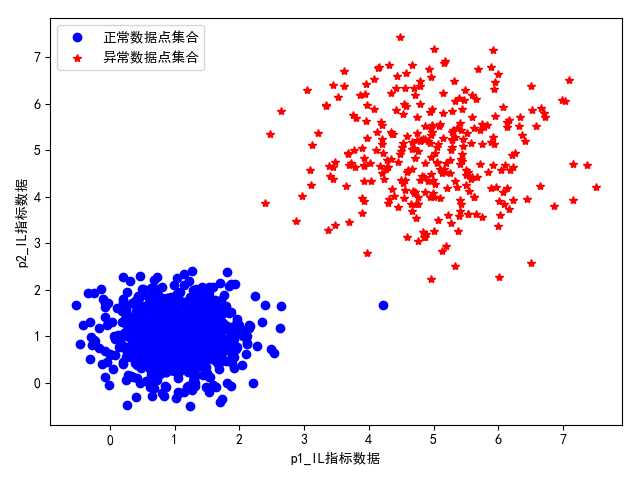
图 正常数据集合和未知异常数据集合数量比为10:3
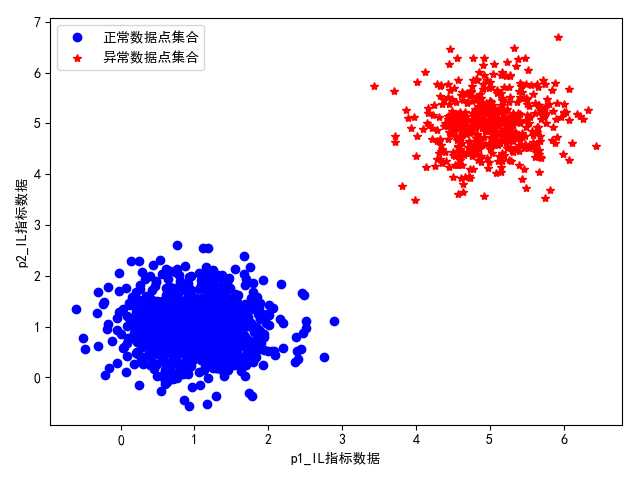
图 正常数据集合和未知异常数据集合数量比为2:1
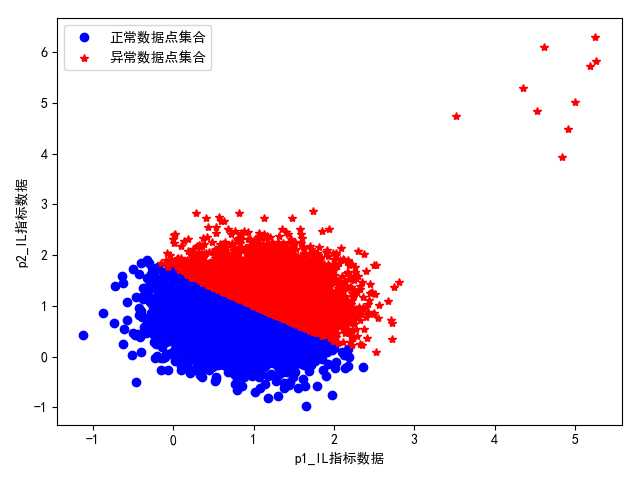
图 正常数据集合和未知异常数据集合数量比为1000:1
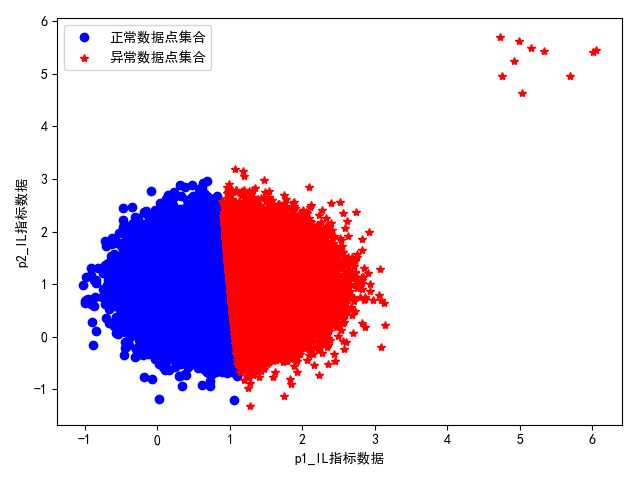
图 正常数据集合和未知异常数据集合数量比为10000:1
基于以上的测试结果可以得到以下的结论:
第一,当正常数据与异常数据数量相差不太大时(数量相对比例在100:1到1:1之间),此时采用算法时会得到非常准确的聚类结果,并且随着二者数量的越来越接近,其分类准确度越高,这也是k-means算法的优越性和适用性所在;
第二,当正常数据点集合和异常数据点集合相差非常大时(数量比例在100:1以上),即正常数据点集合的数目非常多,而异常数据点的集合非常少,此时如果直接采用k-means算法直接进行聚类,可以看到其聚类结果是不合理的,说明此时直接采用聚类算法是不对的,需要对其进行改进,使得其适合这种情况。
②改进版本的k-means聚类方法
通过总结可以看到,在 WSS指标正常数据和未知异常数据的指标特征数据分布范围差异较大,且具有明显的集群相似性的前提下,如果正常数据点集合和异常数据点集合数量相差非常大时(数量比例在100:1以上),即正常数据点集合的数目非常多,而异常数据点的集合非常少时,直接采用k-means聚类算法进行聚类是不合理的,针对这种情况,需要对k-means算法进行一定的改进使用,使得其也可以适用于此种情况。
<1>改进思路
通过上面的聚类结果可以看出,此时k-means算法会因为其异常数据点的数目太少而将其与一部分的正常数据集分到同一类,使得两大类的分类结果数量比较接近,最终造成了聚类判断结果的混淆和不合理。
另外,在分类结果中,可以看到正常数据集合的那一部分聚类结果其实是合理的,也是非常集中的,即各个数据点到聚类中心的距离大小比较接近,相差不大;而包含异常数据点集合的另外一类聚类集合,其数据集合中异常点数据集到聚类中心的距离要远大于其他正常点数据集到聚类中心的聚类,所以可以在聚类结束后计算两大聚类集合中每一个数据点到每一类聚类中心的距离,然后找到存在计算出所有距离最大的一类数据集,即为存在异常数据集的类别集合。
之后,我们将该类中每个数据点到聚类中心的距离进行保存和分布展示,其一般会符合正态分布。根据概率与统计理论,极少的异常数据集到聚类中心的距离一定分布在整体距离集合分布的最外侧
根据正态分布数据的分布特点可知数据分布在[mean-3std,mean+3std]区间的概率为99.74%。因此,基于此理论可知道这些异常点数据集合到聚类中心的距离数据分布此时一定是在这个分布区间以外的,因此找到距离大于mean+3std的点,即为异常点数据集合。
<2>改进算法的具体步骤
第一,针对数据集合首先进行k-means聚类(分两类);
第二,计算两大类数据集合到各自聚类中心的距离;
第三,比较两大类数据集到聚类中心的距离的最大值,最大值存在的聚类类别即为存在异常数据集的集合;
第四,计算存在异常数据点集合类别的距离的平均值mean和标准差std,然后找到距离大于mean+3std的点,则判断为异常点。
<3>改进算法实现结果展示:
针对之前正常数据与异常数据集合数量相差较大时k-means算法存在的问题,我们采用改进版本的k-means算法进行异常数据的判断和输出,其结果与原来的直接k-means聚类结果对比如下所示:
1> 正常数据集合和未知异常数据集合数量比为1000:1时:
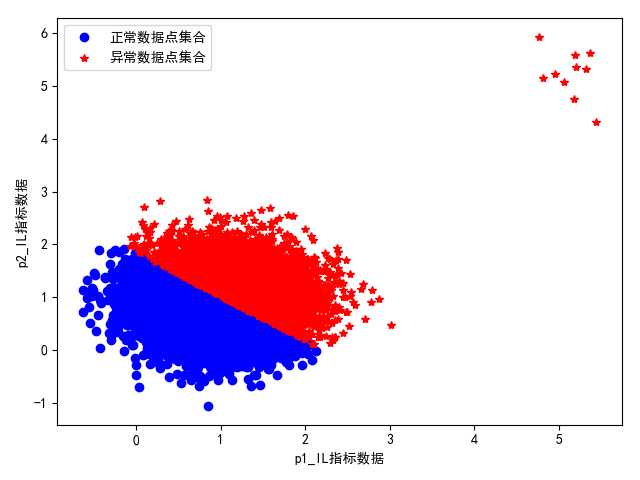
图 k-means直接聚类结果展示(不合理)
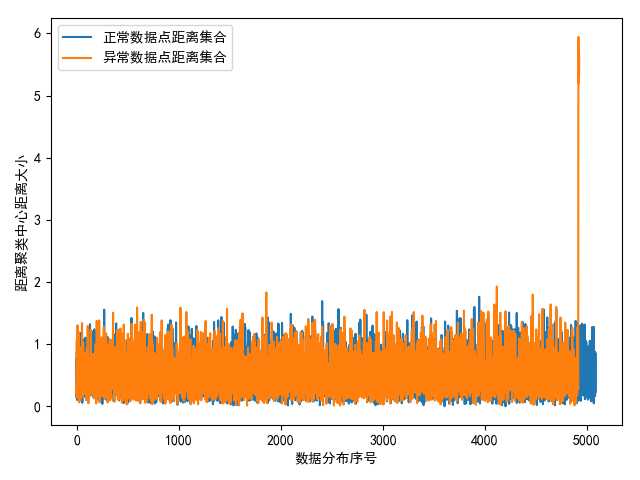
图 正常数据集合和异常数据集合到各自聚类中心的距离分布
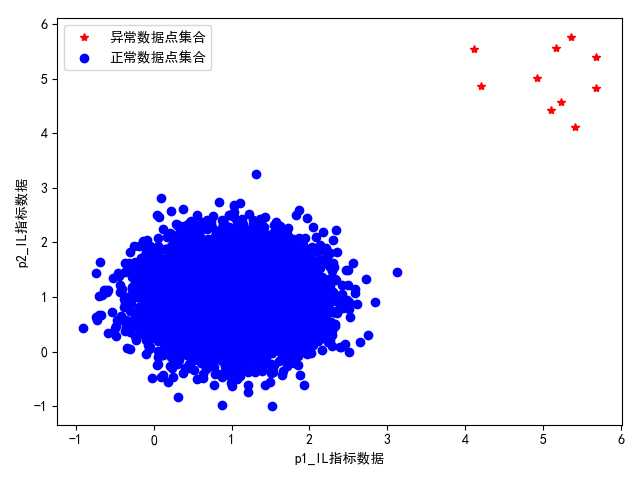
图 改进版本k-means算法的聚类输出结果展示(合理)
2> 正常数据集合和未知异常数据集合数量比为10000:1时:
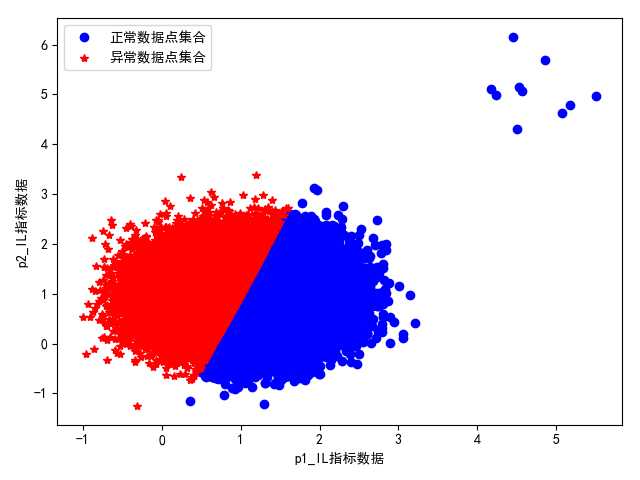
图 k-means直接聚类结果展示(不合理)
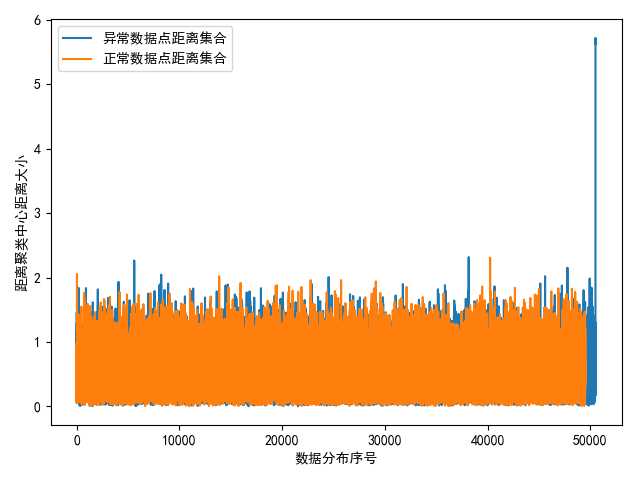
图 正常数据集合和异常数据集合到各自聚类中心的距离分布
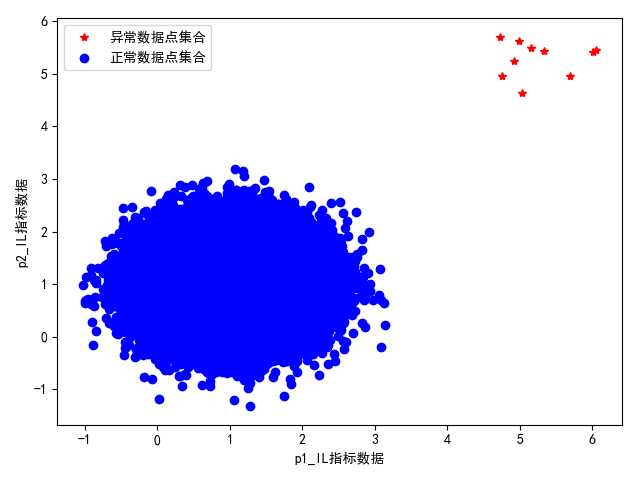
图 改进版本k-means算法的聚类输出结果展示(合理)
另外,需要注意的是,在测试中还可以发现,因为直接聚类之后存在异常数据点的一类和一部分正常数据进行了混合,所以有时候异常检测出来的距离处在mean+3std以外的数据会包含一部分正常数据,因此,为了筛选更加准确,可以将其筛查阈值放的更加大一点,通过测试调整为mean+x*std(其中x处在6-10之间)效果会更加合理一些。
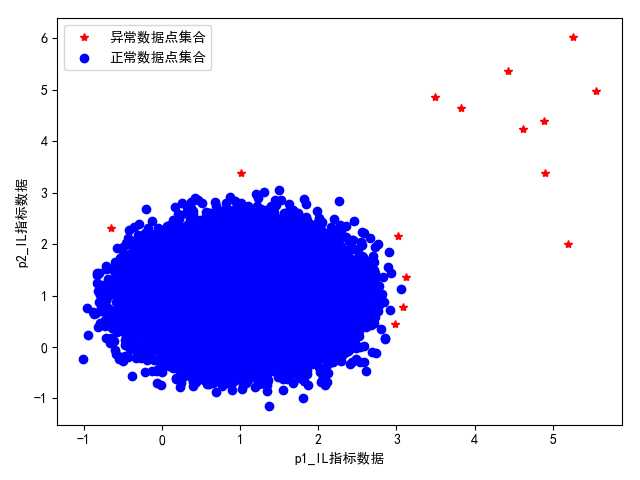
图 设置异常数据点输出的距离判断阈值为mean+3std
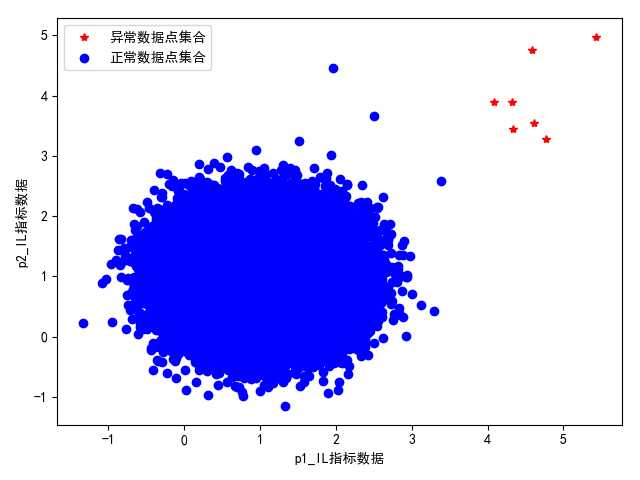
图 设置异常数据点输出的距离判断阈值为mean+8std
标签:因此 均值 转换 随机选择 智能 建立 步骤 测试 margin
原文地址:https://www.cnblogs.com/Yanjy-OnlyOne/p/13362501.html