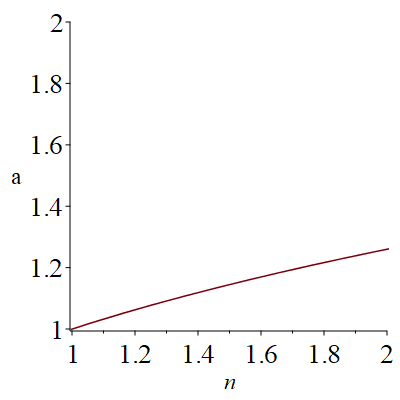标签:解答 class 使用 速度 display load end 这一 面积
1 建立数学模型
1.3 包饺子
-
复习题二
-
假设饺子越大面皮越厚,并且成正比例关系,即
\[\begin{align*}
SH &= n(sh) \H &= a h
\end{align*}
\]
由此可以得到大饺子和小饺子的面皮面积满足
\[S = \frac{n}{a}s
\]
根据教材中的中间结论
\[\begin{align*}
V &= kS^{\frac{3}{2}},& v =ks^{\frac{3}{2}}
\end{align*}
\]
可以得到饺子馅体积的关系满足
\[V = (\frac{n}{a})^{\frac{3}{2}}v = \sqrt{\frac{n}{a^3}}(nv)
\]
显然,在这个新的 \(V-nv\) 关系中,“饺子数量减少一倍能多包多少馅”的回答是与厚度变化系数\(a\)相关的:
- 当\(a = \sqrt[3]{2} \approx 1.26\)时,能包的馅数量不变;
- 当\(a > 1.26\)时,能包的馅变少;
- 当\(a<1.26\)时,能包的馅增加。
可以发现,厚度变化系数 \(a\) 存在一个临界值 \(\sqrt[3]{n}\) ,当它大于临界值时,能包的馅反而少了,反之则会更多。为了更好地观察这一临界值的变化,我们可以作出饺子数量变化倍数\(n\)与\(a\)临界值的关系图:
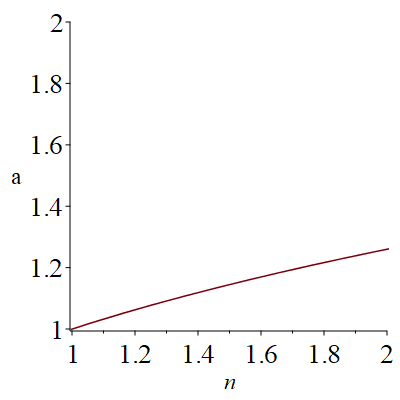
2 初等模型
2.2 滑艇比赛的成绩
复习题
考虑八人艇分重量组(桨手体重不超过86 kg)个轻量级组(桨手体重不超过73 kg),建立模型说明重量组的成绩比轻量组的大约好 5%.
考虑艇重
使用与书中相同的假设。
根据桨手输出的功率与阻力 \(f\) 和速度 \(v\) 的乘积成正比,有
\[\begin{equation}
np \propto fv
\label{2.2.1}
\end{equation}
\]
根据假设2,3,可得
\[\begin{align}
f &\propto sv^2 &p \propto w
\end{align}
\]
代入\(\eqref{2.2.1}\)式,可得
\[\begin{equation}
v \propto (\frac{nw}{s})^\frac{1}{3}
\label{2.2.3}
\end{equation}
\]
教材中已经得到浸没面积 \(s\) 与艇手数 \(n\) 的关系
\[\begin{equation}
s \propto n^\frac{2}{3}
\label{2.2.2}
\end{equation}
\]
加入艇手体重和艇重,式\(\eqref{2.2.2}\)进一步写为
\[s \propto (kn+nw)^\frac{2}{3}
\]
其中,\(k\) 是艇重与艇手数的比例系数.
代入\(\eqref{2.2.3}\)式,并考虑到同为八人艇,消去 $ n$,可以得到速度与艇手重量 \(w\) 的关系
\[v \propto \frac{w^\frac{1}{3}}{(w+k)^\frac{2}{9}}
\]
因为比赛成绩 \(t\) 与 \(v\) 成反比,所以
\[\begin{equation}
t \propto \frac{(w+k)^\frac{2}{9}}{w^\frac{1}{3}}\propto(\frac{1}{w}+\frac{2k}{w^2}+\frac{k^2}{w^3})^\frac{1}{9}
\label{2.2.4}
\end{equation}
\]
由表1中最后一列的数据可知,对于八人艇,\(w_0=14.7n\),即\(k=14.7\). 代入\(\eqref{2.2.4}\)式,可得
\[t \propto(\frac{1}{w}+\frac{29.4}{w^2}+\frac{216.09}{w^3})^\frac{1}{9}
\]
最终,可以得到重量组和轻量组的相对成绩差为
\[\delta = \frac{t_{73}-t_{86}}{t_{73}} \approx 2.4\%
\]
不考虑艇重
使用与书中相同的假设。
根据桨手输出的功率与阻力 \(f\) 和速度 \(v\) 的乘积成正比,有
\[\begin{equation}
np \propto fv
\label{2.2.5}
\end{equation}
\]
根据假设2,3,可得
\[\begin{align}
f &\propto sv^2 &p \propto w
\end{align}
\]
代入\(\eqref{2.2.5}\)式,可得
\[\begin{equation}
v \propto (\frac{nw}{s})^\frac{1}{3}
\end{equation}
\label{2.2.7}
\]
教材中已经得到浸没面积 \(s\) 与艇手数 \(n\) 的关系
\[\begin{equation}
s \propto n^\frac{2}{3}
\end{equation}
\label{2.2.6}
\]
加入艇手体重和艇重,\(\eqref{2.2.6}\)式进一步写为
\[s \propto (nw)^\frac{2}{3}
\]
代入\(\eqref{2.2.7}\)式,并考虑到同为八人艇,消去 $ n$,可以得到速度与艇手重量 \(w\) 的关系
\[v \propto w^\frac{1}{9}
\]
因为比赛成绩 \(t\) 与 \(v\) 成反比,所以
\[t \propto w^{-\frac{1}{9}}
\]
最终,可以得到重量组和轻量组的相对成绩差为
\[\delta = \frac{73^{-\frac{1}{9}} - 86^{-\frac{1}{9}}}{73^{-\frac{1}{9}}} \approx 1.8 \%
\]
习题解答——姜启源《数学模型》
标签:解答 class 使用 速度 display load end 这一 面积
原文地址:https://www.cnblogs.com/zxlzxl/p/13373180.html