2020杭电多校第2场

时间：2020-07-24 21:43:59 阅读：171 评论：0 收藏：0 [点我收藏+]

标签：items 代码 online dfs unset printf bool 官方 img

由于本人水平不够，这场多校只写了第1题和第10题

第1题

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6763

Problem A. Total Eclipse

　　There are n cities and m bidirectional roads in Byteland. These cities are labeled by 1, 2, . . . , n, the

　　brightness of the i-th city is bi.

　　Magician Sunset wants to play a joke on Byteland by making a total eclipse such that the brightness of

　　every city becomes zero. Sunset can do the following operations for arbitrary number of times:

　　　　• Select an integer k (1 ≤ k ≤ n).

　　　　• Select k distinct cities c1, c2, . . . , ck (1 ≤ ci ≤ n) such that they are connected with each other. In other words, for every pair of distinct selected cities ci and cj (1 ≤ i < j ≤ k),

　　　　if you are at city ci,you can reach city cj without visiting cities not in {c1, c2, . . . , ck}.

　　　　• For every selected city ci (1 ≤ i ≤ k), decrease bci by 1.

　　Now Sunset is wondering what is the minimum number of operations he needs to do, please write a program to help him

Input

　　The fifirst line of the input contains a single integer T (1 ≤ T ≤ 10), the number of test cases.

　　For each case, the fifirst line of the input contains two integers n and m (1 ≤ n ≤ 100 000, 1 ≤ m ≤ 200 000),denoting the number of cities and the number of roads.

　　The second line of the input contains n integers b1, b2, . . . , bn (1 ≤ bi ≤ 109 ), denoting the brightness of each city.

　　Each of the following m lines contains two integers ui and vi (1 ≤ ui , vi≤ n, ui= vi), denoting an bidirectional road between the ui-th city and the vi-th city. Note that there may be multiple roads

　　between the same pair of cities.

Output

　　For each test case, output a single line containing an integer, the minimum number of operations.

题意：给定一个无向图，每个点给定权值，每次选择一个连通块，将连通块里面所有点权值同时减1，直到所有点权值都变成 0，问最少需要几次

解题思路（官方题解）：

　　　　每次一定是选择一个极大连通块，将里面所有数同时减小，直到最小值变成 0，然后将变成 0 的点删除，分裂成多个连通块再接着做。

　　　　为了实现这个策略，可以将整个过程倒过来看，变成按照 b 的值从大到小依次加入每个点。加入每个点 x 时遍历与 x 相连的所有边 (x, y)，如果 y 在 x 之前加入且 x 和 y 不连通则将 x

　　和 y 合并，并将 y 所在连通块的树根的父亲设为 x，得到一棵有根树。那么每个点 x 在成为最

　　小值之前已经被做了 bfatherx 次操作，所以每个点 x 对答案的贡献为 bx-bfatherx。

　　　　使用并查集支持路径压缩，时间复杂度 O((n + m)log n)。

代码：

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 const int N=1e5+5;
 4 struct node
 5 {
 6     int id,bi;
 7 }ss[N];
 8 int f[N],fa[N],b[N];
 9 bool vis[N];
10 vector<int > vec[N];
11 int n,m;
12 int find(int x)
13 {
14     if(f[x]==x)return x;
15     return f[x]=find(f[x]);
16 }
17 void init()
18 {
19     memset(vis,0,sizeof(vis));
20     memset(fa,0,sizeof(fa));
21     for(int i=0;i<N;i++)
22         f[i]=i,vec[i].clear();
23 }
24 bool cmp(struct node x,struct node y)
25 {
26     return x.bi>y.bi;
27 }
28 
29 int main()
30 {
31     int t;
32     scanf("%d",&t);
33     while(t--)
34     {
35         init();
36         scanf("%d%d",&n,&m);
37         for(int i=1;i<=n;i++)
38         {
39             scanf("%d",&b[i]);
40             ss[i].bi=b[i];
41             ss[i].id=i;
42         }
43         sort(ss+1,ss+1+n,cmp);
44         int u,v,father;
45         for(int i=0;i<m;i++)
46         {
47             scanf("%d%d",&u,&v);
48             vec[u].push_back(v);
49             vec[v].push_back(u);
50         }
51         for(int i=1;i<=n;i++)
52         {
53             u=ss[i].id;
54             vis[u]=1;
55             int len=vec[u].size();
56             for(int j=0;j<len;j++)
57             {
58                 v=vec[u][j];
59                 if(vis[v]==0)continue;
60                 father=find(v);
61                 if(father==u)continue;
62                 fa[father]=f[father]=u;
63             }
64         }
65         long long ans=0;
66         for(int i=1;i<=n;i++)
67             ans+=b[i]-b[fa[i]];
68         printf("%lld\n",ans);
69     }
70     return 0;
71 }

代码

第10题

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6763

Problem J. Lead of Wisdom

　　In an online game, “Lead of Wisdom” is a place where the lucky player can randomly get powerful items.

　　There are k types of items, a player can wear at most one item for each type. For the i-th item, it has

　　four attributes ai , bi , ci and di . Assume the set of items that the player wearing is S, the damage rate of

　　the player DMG can be calculated by the formula:

　　Little Q has got n items from “Lead of Wisdom”, please write a program to help him select which items to wear such that the value of DMG is maximized.

Input

　　The fifirst line of the input contains a single integer T (1 ≤ T ≤ 10), the number of test cases.

　　For each case, the fifirst line of the input contains two integers n and k (1 ≤ n, k ≤ 50), denoting the number of items and the number of item types.

　　Each of the following n lines contains fifive integers ti , ai , bi , ci and di (1 ≤ ti ≤ k, 0 ≤ ai , bi , ci , di ≤ 100),

　　denoting an item of type ti whose attributes are ai , bi , ci and di.

Output

　　For each test case, output a single line containing an integer, the maximum value of DMG.

题意：每组选一个，使DMG最大

题解：暴力

我的代码写的太丑了，这里就不给出了

官方题解代码：

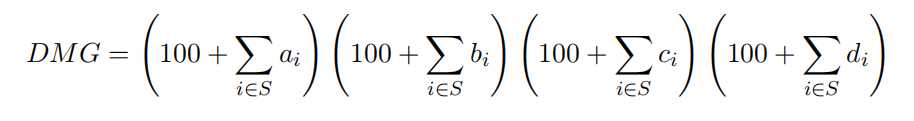
 1 #include<cstdio>
 2 typedef long long ll;
 3 const int N=55;
 4 int Case,n,m,i,j,x,cnt[N],nxt[N],e[N][N][4];ll ans;
 5 void dfs(int x,int a,int b,int c,int d){
 6   if(x>m){
 7     ll tmp=1LL*a*b*c*d;
 8     if(tmp>ans)ans=tmp;
 9     return;
10   }
11   int num=cnt[x];
12   if(!num){
13     dfs(nxt[x],a,b,c,d);
14     return;
15   }
16   for(int i=1;i<=num;i++)dfs(x+1,a+e[x][i][0],b+e[x][i][1],c+e[x][i][2],d+e[x][i][3]);
17 }
18 int main(){
19   scanf("%d",&Case);
20   while(Case--){
21     scanf("%d%d",&n,&m);
22     for(i=1;i<=m;i++)cnt[i]=0;
23     while(n--){
24       scanf("%d",&x);
25       cnt[x]++;
26       for(j=0;j<4;j++)scanf("%d",&e[x][cnt[x]][j]);
27     }
28     x=m+1;
29     for(i=m;i;i--){
30       nxt[i]=x;
31       if(cnt[i])x=i;
32     }
33     ans=0;
34     dfs(1,100,100,100,100);
35     printf("%lld\n",ans);
36   }
37 }

代码

2020杭电多校第2场

标签：items 代码 online dfs unset printf bool 官方 img

原文地址：https://www.cnblogs.com/zenghuan0620/p/13374176.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行