POJ-2516 Minimum Cost(最小费用最大流)

标签：puts   min   turn   alt   http   ==   cpp   return   inf   

题意:有n个商店，卖k种物品，有m个供应商，不同的供货商存货不同，不同商店对不同需求量也不同，运输的费用也不同，求满足所有店主要求的最小运输费用。

分析:样例中的数据解释:。
供应是否满足需求的条件?
1.每种物品的总供应量>=每种物品的总需求量
如何求k种物品的总的最小费用？我们可以跑k次费用流，求总和。
样例中求运送第一种物品的建图如下:

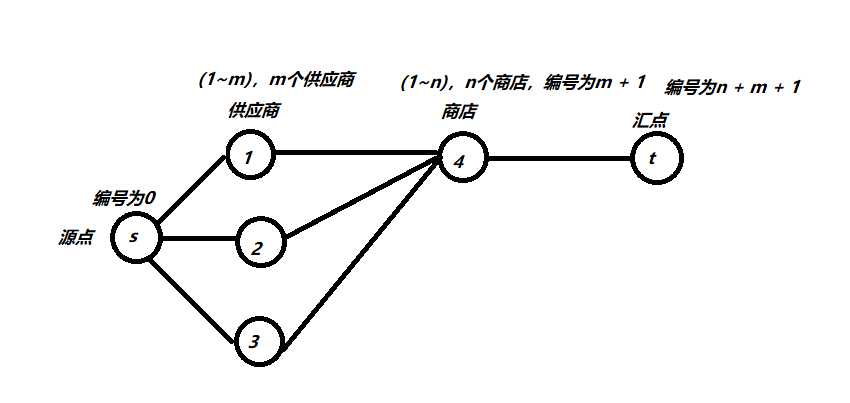
源点和供应商的每条边的容量为供应商供应这个物品的总量，费用为0。供应商和商店之间的每条边的容量为供应商供应这个物品的总量以及费用为从这个供应商运送这个物品到这个商店的费用。从商店到汇点的每条边的容量为这个商店对这个商品的需求量。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <vector>
#include <queue>
#include <algorithm>

using namespace std;
const int N = 305;
//n个商店，m个供应商，k种物品
int n, m, k;

//每家商店的需求清单
int shop[N][N];
//每家供应商的提供
int supply[N][N];

//每种物品的需求量
int totn[N];
//每种物品的供应量
int tots[N];

int off[N][N][N];

const int M = 300 * N;
int s, t, maxflow, res;

int h[M], e[M * 2], ne[M * 2], w[M * 2], cost[M * 2], idx;
int d[M * 2], incf[M * 2], pre[M * 2];
bool st[M * 2];

void add(int a, int b, int z, int c)
{
	e[idx] = b, w[idx] = z, cost[idx] = c, ne[idx] = h[a], h[a] = idx++;
	e[idx] = a, w[idx] = 0, cost[idx] = -c, ne[idx] = h[b], h[b] = idx++;
}

bool spfa()
{
	queue<int> q;
	q.push(s);
	memset(d, 0x3f, sizeof d);
	memset(st, 0, sizeof st);
	d[s] = 0, st[s] = true;
	incf[s] = 1 << 30;

	while (q.size())
	{
		int u = q.front();
		q.pop();
		st[u] = false;
		for (int i = h[u]; i != -1; i = ne[i])
		{
			int j = e[i];
			if (!w[i]) continue;
			if (d[j] > d[u] + cost[i])
			{
				d[j] = d[u] + cost[i];
				incf[j] = min(incf[u], w[i]);
				pre[j] = i;
				if (!st[j])
				{
					st[j] = true;
					q.push(j);
				}
			}
		}
	}
	if (d[t] == 0x3f3f3f3f) return false;
	return true;
}

void update()
{
	int u = t;
	while (u != s)
	{
		int i = pre[u];
		w[i] -= incf[t];
		w[i ^ 1] += incf[t];
		u = e[i ^ 1];
	}
	maxflow += incf[t];
	res += d[t] * incf[t];
}

void init()
{
	maxflow = 0, idx = 0;
	memset(h, -1, sizeof h);
}

void clear()
{
	memset(shop, 0, sizeof shop);
	memset(totn, 0, sizeof totn);
	memset(tots, 0, sizeof tots);
	res = 0;
}

int main()
{	
	while (scanf("%d%d%d", &n, &m, &k) != EOF)
	{
		if (n == 0 && m == 0 && k == 0) break;
		clear();
		bool flag = true;
		for (int i = 1; i <= n; ++i)
		{
			//每家商店的需求清单
			for (int j = 1; j <= k; ++j)
			{
				scanf("%d", &shop[i][j]);
				totn[j] += shop[i][j];
			}
		}

		for (int i = 1; i <= m; ++i)
		{
			//每家供应商的提供
			for (int j = 1; j <= k; ++j)
			{
				scanf("%d", &supply[i][j]);
				tots[j] += supply[i][j];
			}
		}

		for (int i = 1; i <= k; ++i)
		{
			if (tots[i] < totn[i])
			{
				flag = false;
				break;
			}
		}

		//k个矩阵
		for (int u = 1; u <= k; ++u)
		{
			for (int i = 1; i <= n; ++i)
			{
				for (int j = 1; j <= m; ++j)
				{
					//第j个供应商运送1单元的k货物到第i个商家的费用
					scanf("%d", &off[u][j][i]);
				}
			}
		}

		if (!flag)
		{
			puts("-1");
			continue;
		}
		else
		{
			s = 0, t = m + n + 1;
			
			//求k次最小费用最大流
			for (int u = 1; u <= k; ++u)
			{
				init();

				for (int i = 1; i <= m; ++i)
				{
					add(s, i, supply[i][u], 0);
				}

				//供应商向商家供货
				for (int i = 1; i <= m; ++i)
				{
					for (int j = 1; j <= n; ++j)
					{
						add(i, m + j, supply[i][u], off[u][i][j]);
					}
				}

				for (int i = 1; i <= n; ++i)
				{
					add(m + i, t, shop[i][u], 0);
				}

				while (spfa()) update();
			}

			printf("%d\n", res);
		}
	}


	return 0;
}

POJ-2516 Minimum Cost(最小费用最大流)

标签：puts   min   turn   alt   http   ==   cpp   return   inf   

原文地址：https://www.cnblogs.com/pixel-Teee/p/13374126.html