标签:效率 under capacity 替换 实现机制 htm 不能 lis 过滤
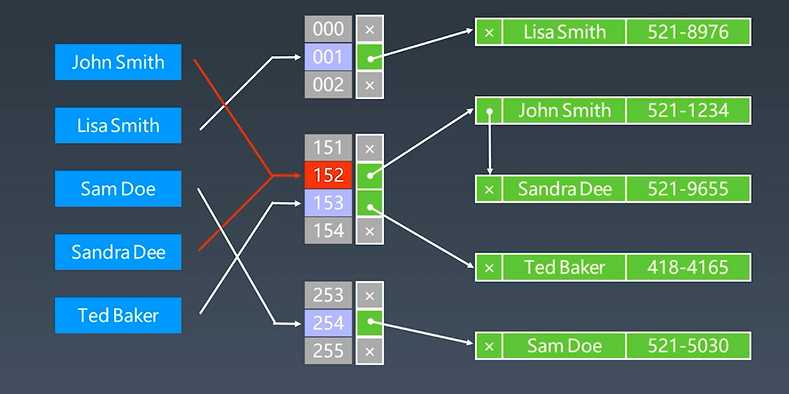
布隆过滤器和哈希表类似,HashTable + 拉链表存储重复元素:
元素 ---哈希函数---> 映射到一个整数的下标位置index。比如Join Smith和Sandra Dee经过哈希函数都映射到了152的下标,就在152的位置开一个链表,把多个元素都存在相同位置的链表处,往后边不断的积累积累。
它不仅有哈希函数得到一个index值,且会把整个要素的元素都存储到哈希表里边去,这是一个没有误差的数据结构,有多少个元素,每个元素有多大,所有这些元素所占的内存空间等在哈希表里边都要有相应的内存大小给存储起来。
但是在很多工业级应用中,我们并不需要存储所有的元素本身,而只需要存储一个信息,即这个元素在这个表里边有没有,这时就需要更高效的一种数据结构。
布隆过滤器即 一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否存在一个集合中。(而哈希表不只是判断元素是否在一个集合中,同时还可以存元素本身和元素的各种额外信息。布隆过滤器只用于检索一个元素它是否在还是不在的信息,而不能存其它的额外信息)
优点:空间效率和查询时间都远远超过一般的算法,
缺点是有一定的误识别率和删除困难。
布隆过滤器示意图:
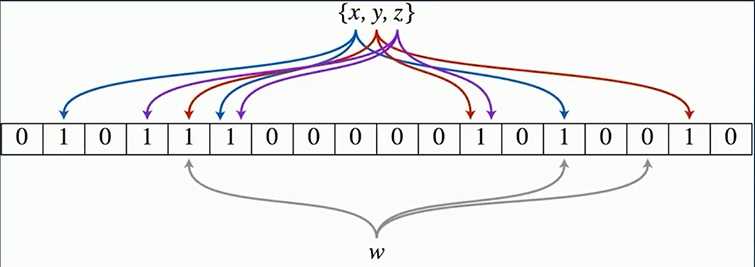
x,y,z不是同时往里边添加,一个一个的添加; 每一个元素它会分配到一系列的二进制位中。
假设x会分配3个二进制位,蓝色线表示, 把x插入布隆过滤器时即把x对应的这三个位置置为1就可以了。
y插入进来,根据它的哈希函数分为红色的这三条线所对应的二进制位,置为1。
同理z也置为1。
这个二进制的数组用来表示所有的已经存入的xyz是否已经在索引里边了。
重新插入一个x, 这时x始终会对应这3个蓝色的二进制位, 去表里查就查到这三个都是1, 所以我们认为x是存在的。
如果是一个陌生的元素w进来, 它把它分配给通过布隆过滤器的二进制索引的函数, w就得到灰色的这三个二进制位110, 有一个为0说明w未在索引里边。
只要布隆过滤器中有一个为0就说明这个元素不在布隆过滤器的索引里面, 且我们肯定它不在。
但比如又来一个元素q, 它刚好分配的三个二进制都为1, 我们不一定说它是存在的。
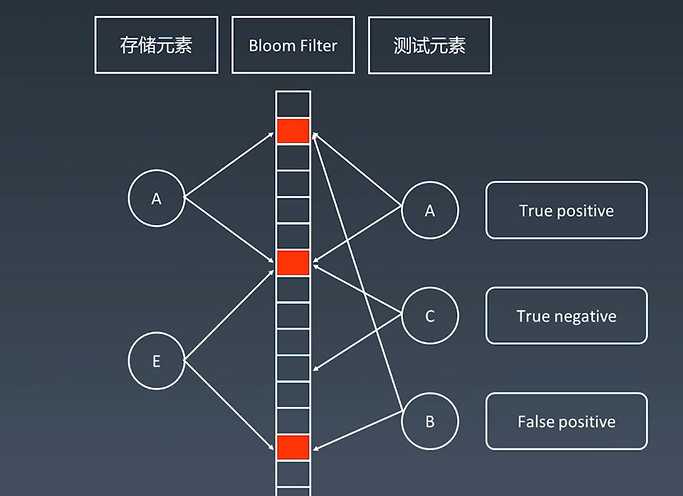
存储元素A和E都存入布隆过滤器中,置为1.
测试元素,A查到到它的二进制位为1,可能是有的;C查到它的二进制位有一个为0,则C肯定不在布隆过滤器里边;B恰好分配的二进制位都为1,但从来没有存储过B,则我们会判断B在这个索引里边,这个时候对于B的判断就是有误差的。
结论:
当布隆过滤器把元素全部插入完之后, 对于测试(新来)的元素要验证它是否存在
当它验证这个元素所对应的二进制位是1时, 我们只能说它可能存在布隆过滤器里边。
但是当这个元素所对应的二进制位只要有一个不为1, 则它肯定不在。
---一个元素去布隆过滤器里边查, 如果查到它不存在, 那么它肯定就是不存在的。
如果查到它的二进制都是1,为存在的状态比如B,则它可能存在。
那我们到底怎么判断B这种元素是否存在呢?
布隆过滤器只是放在外边当一个缓存使用,来作为一个很快速的判断来使用
当B查到了,布隆过滤器里边是存在的,则B会继续在这个机器上的数据库DB中来查询,去查询B是否存在。
而C就会直接打到布隆过滤器里边,这样C就不用查询了节省了查询访问数据库的时间。
布隆过滤器只是挡在一台机器前边的快速查询的缓存。
案例
①.比特币网络
②.分布式系统(Map-Reduce) -- Hadoop、 Searchengine
③.Redis缓存
④.垃圾邮件、评论等的过滤
https://www.cnblogs.com/cpselvis/p/6265825.html
https://blog.csdn.net/tianyaleixiaowu/article/details/74721877
布隆过滤器的Java代码实现:
https://github.com/lovasoa/bloomfilter/blob/master/src/main/java/BloomFilter.java
https://github.com/Baqend/Orestes-Bloomfilter
①.记忆
②.钱包-储物柜
③.代码模块
Understanding the Meltdown exploit – in my own simple words
上图为四核CPU,三级缓存(L1 Cache,L2 Cache ,L3 Cache);
每一个核里边就有L1 D-Cache,L1 l-Cache,L2 Cache,L3 Cache;最常用的数据马上要给CPU的计算模块进行计算处理的就放在L1里边,次之不常用的就放在L1 l-Cache里边,再次之放在L2Cache里边,最后放在L3 Cache里边。外边即内存。他们的速度 L1 D-Cache > L1 l-Cache > L2-Cache > L3-Cache
体积(能存的数据多少)即 L1 D-Cache < L1 l-Cache < L2-Cache < L3-Cache
两个要素:
大小
替换策略(least recent use -- 最近最少使用)
实现机制:
HashTable+DoubleLinkedList
复杂度分析:
O(1)查询
O(1)修改、 更新
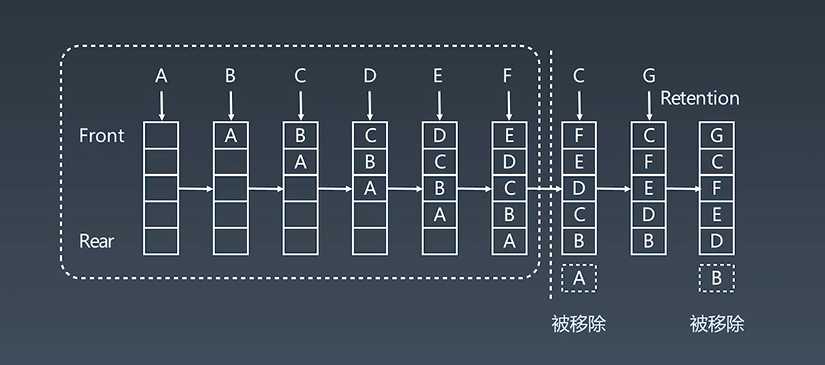
LRU Cache工作示例:
更新原则 least recent use
替换策略:
LFU - least frequently used
LRU - least recently used
LRUCache Python
class LRUCache(object):
def __init__(self, capacity):
self.dic = collections.OrderedDict()
self.remain = capacity
def get(self, key):
if key not in self.dic:
return -1
v = self.dic.pop(key)
self.dic[key] = v # key as the newest one
return v
def put(self, key, value):
if key in
self.dic: self.dic.pop(key)
else:
if self.remain > 0:
self.remain -= 1
else: # self.dic is full
self.dic.popitem(last=False)
self.dic[key] = value
LRUCache Java
private Map<Integer, Integer> map;
public LRUCache(int capacity) {
map = new LinkedCappedHashMap<>(capacity);
}
public int get(int key) {
if (!map.containsKey(key)) {
return -1;
}
return map.get(key);
}
public void put(int key, int value) {
map.put(key, value);
}
private static class LinkedCappedHashMap<K, V> extends LinkedHashMap<K, V> {
int maximumCapacity;
LinkedCappedHashMap(int maximumCapacity) {
// initialCapacity代表map的容量, loadFactor代表加载因子, accessOrder默认false,如果要按读取顺序排序需要将其设为true
super(16, 0.75f, true);//default initial capacity (16) and load factor (0.75) and accessOrder (false)
this.maximumCapacity = maximumCapacity;
}
/* 重写 removeEldestEntry()函数,就能拥有我们自己的缓存策略 */
protected boolean removeEldestEntry(Map.Entry eldest) {
return size() > maximumCapacity;
}
}
标签:效率 under capacity 替换 实现机制 htm 不能 lis 过滤
原文地址:https://www.cnblogs.com/shengyang17/p/13341128.html