标签:The mamicode cin src 错误 load 端点 line cti
本文发表半小时后,我百度搜索,想看一下其他人的文章,结果发现本文,排名搜索结果第一名
截图在文章最后
英语单词: lagrange mean value theorem
auxiliary function
construction of the auxiliary function
有多种构造方法, 辅助函数不止一个
一,几何方法
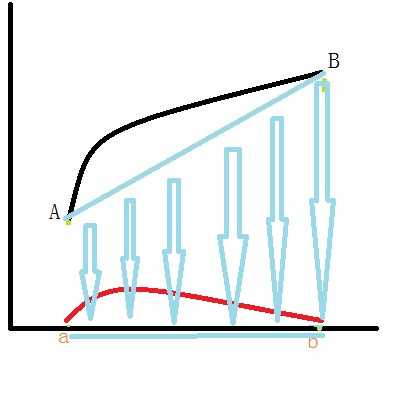
思路:设构造出的辅助函数为F,必须有F(a)=F(b)=0,才能应用罗尔中值定理
\(让f(x)在[a,b]区间内的所有点,下移直线弦AB到x轴的距离,即可保证弦AB跟x轴重回。\)
\(弦AB与x轴重合,即,F(a)=F(b)=0.\)
\(这个距离是一个跟x有关的函数,这个函数\\\)
\(就是弦AB的直线段的函数:g(x)=kx+b\)
\(由:f(a)=ka+b,f(b)=kb+b,\)
\(解得,k=\frac{f(b)-f(a)}{b-a}\)
\(\quad\quad b=f(a)-\frac{f(b)-f(a)}{b-a}a\)
\(弦方程为:y=\frac{f(b)-f(a)}{b-a}x+f(a)-\frac{f(b)-f(a)}{b-a}a\)
\(合并同类项:y=f(a)+\frac{f(b)-f(a)}{b-a}(x-a)\)
让F(x)减去弦的高度,即上式的弦方程,即可做到f(x)曲线的右端点B,落在x轴上
\(即:F(x)=f(x)-f(a)-(\frac{f(b)-f(a)}{b-a}x+f(a)-\frac{f(b)-f(a)}{b-a}a)\)
\(化简为:F(x)=f(x)-f(a)-\frac{f(b)-f(a)}{b-a}(x-a)\)
上式与拉格朗日中值定理的辅助函数,完全一致
\(【注意】有网友认为是曲线先下落,然后以(a,0)点为轴,旋转曲线右端点到x轴,这是错误的。\\\)
\(因为旋转是弧形旋转,弦AB长度不变,实际是长度缩短了,因为是投影下来的,曲线两端点的距离不变\)
参考文献
余惠霖的文章
https://wenku.baidu.com/view/403bd330ff00bed5b8f31d0f.html


天水师范学院常正军的毕业论文
https://www.docin.com/p-694641420.html
本文搜索排名第一的截图如下
标签:The mamicode cin src 错误 load 端点 line cti
原文地址:https://www.cnblogs.com/strongdady/p/13379248.html