O(nlogn)求出最长不上升子序列的长度

标签：调试器   efault   模拟   src   cpp   open   读者   tar   data   

1.实现方式

首先我们需要一个数组a，存储从第1个到第n个导弹的高度

然后一个数组d(其实是个栈)，存储不上升序列

把a中的每个元素挨个加到d里面：

(a中第i个元素为a[i]，d长度为len，d中最后一个(也是最小的一个)为d[len])

如果a[i] <= d[len]，说明a[i]可以接在d后面(而整个d还是有序的)，那就简单粗暴地把a[i]丟进d：

d[++len] = a[i]

如果a[i] > d[len]，说明a[i]接不上

但是我们发扬瞎搞精神：接的上要接，接不上创造条件也要接！

强行把a[i]塞进去：

在d中找到第一个小于a[i]的数，把它踹了，用a[i]代替它！(为什么正确在下面）

假设这个数是y，怎样踹掉它呢？

很明显，我们需要使用lower_bound和upper_bound来查找

第一步，找一个听起来无比正确的理由，比如它占着位置不干活啦，干起活来还不如a[i]啦，naive啦，它too young啦，too simple啦......反正能骗过lower_bound和upper_bound就行

(lower_bound&&upper_bound：你当我们傻)(w1049：真聪明)

接下来，特别有正义感的lower_bound和upper_bound就会去把y给拎出来

第二步，考虑使用什么

我们知道，要求的是最大不上升子序列长度，也就是如果两个元素相等也是可以的

所以我们踹人就不用踹等于a[i]的了

结合上面，应该使用upper_bound(终于想起来它了)并且使用>作为比较器(这是个下降序列)

第三步，直接开搞

int p = upper_bound(d + 1, d + 1 + len, a[i], greater<int>()) - d;
  
d[p] = a[i];

成功把a[i]塞了进去

2.为什么正确

显然成立

如果y在末尾，由于y < a[i]，所以y后面能接的不如a[i]多，y让位给a[i]可以让序列更长

如果y不在末尾，那y有生之年都不会再被用到了，直接踹了y就行，y咋样，who care？

注意到lower_bound只能在有序序列中使用，此时d还有序吗？

当然有序。(本文第一个句号)

假设y前一个y1，y后一个是y2，则

y1 > y > y2y1>y>y2

因为y是第一个小于a[i]的，所以

y1 > a[i]y1>a[i]

又因为

a[i] > y > y2a[i]>y>y2

所以

y1 >y1>a[i]> y2>y2

对比下原来的式子

y1 >y1>y> y2>y2

a[i]可以完美代替y，至于y以后咋办，who care？

对于最长上升子序列，只需要把上面的过程通通换一下符号

可以用以下方法证明：

反之亦然同理，推论自然成立，略去过程QED，由上可知证毕(多么美妙的证明)

实际上，d[i]d[i]的含义是：最大不上升子序列长度为ii时，最优的结尾元素。

3.代码：

for(int i=2;i<=n;i++)
	if(d[len]>=a[i])d[++len]=a[i];
	else {
		int p=upper_bound(d+1,d+1+len,a[i],greater<int>())-d;
		d[p]=a[i];
	}

最后len就是要求的最大不上升子序列长度

但要注意的是，d中存储的并不是最大不上升子序列！

原因如下：

即得易见平凡，仿照上例显然，留作习题答案略，读者自证不难

4.对样例模拟：

在这里推荐一下DevC++的调试器(不用DevC++的当我没说)

（还是不要推荐了）

1.我们把a[i]**(389)**加入d：

2.i=2，此时a[i](207)<=d[len](389)，把a[2]加入d：

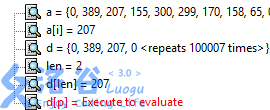
3.i=3，此时a[i](155)<=d[len](207)，把a[3]加入d：

4.i=4，此时a[i](300)>d[len](155)，不能直接加入，所以准备踹人

5.找出d中第一个小于a[i](300)的(即207)，用a[i]换掉

6.i=5，此时a[i](299)>d[len](155)，不能直接加入，所以准备踹人

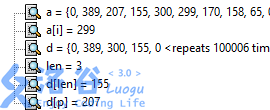
7.找出d中第一个小于a[i](299)的(即155)，用a[i]换掉

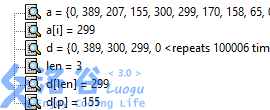
8.i=6，此时a[i](170)<=d[len](299)，把a[6]加入d：

9.i=7，此时a[i](158)<=d[len](170)，把a[7]加入d：

10.i=8，此时a[i](65)<=d[len](158)，把a[8]加入d：

至此，得到最大不上升子序列长度len=6

by——w1049344862

洛谷

——END——

O(nlogn)求出最长不上升子序列的长度

标签：调试器   efault   模拟   src   cpp   open   读者   tar   data   

原文地址：https://www.cnblogs.com/yxr001002/p/13379685.html