标签:返回 返回结果 cpp 难度 clu 题目 导致 date 就会

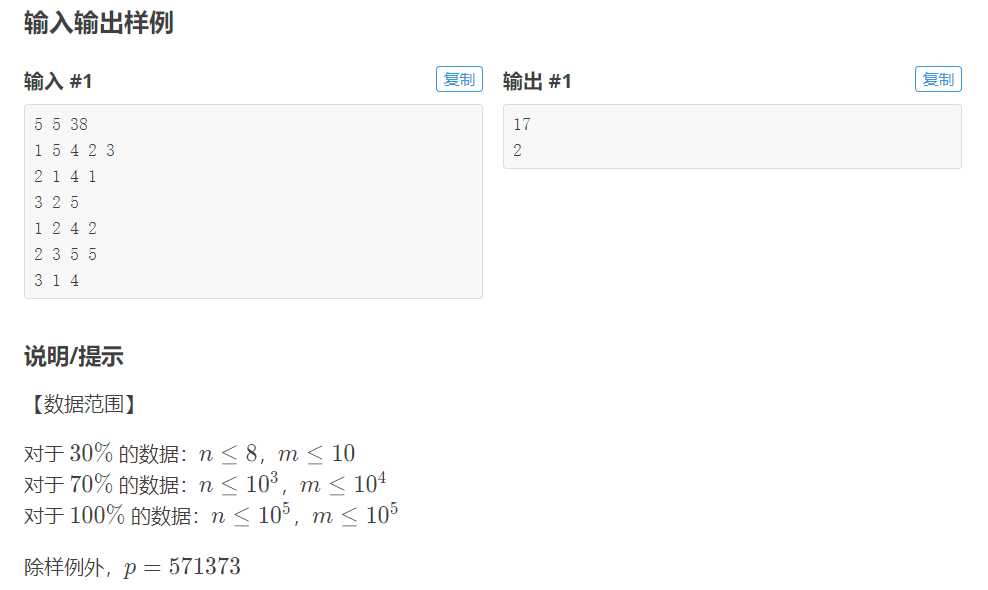
这道题虽然和线段树1同是线段树模板题,但是这道题的难度我个人感觉是比1提高了,主要就是在有关lazytag的处理和运算方面更加复杂。
这道题的有两种修改操作,一种是区间加,一种是区间乘。这就会导致我们使用一个lazytag无法解决所有的问题,所以我们就要维护两个lazytag,一个是加法,另一个是乘法。维护两个lazytag除了增
加了一点码量之外没有什么难的地方,而这道题难就难在如何pushdown上。每次pushdown时乘法和加法的顺序对此题有非常大的影响,所以如果你的pushdown里乘法和加法的顺序是瞎写的,那很有可能会挂。
PS:有可能有人会问题目的更新是一次一次的,而且是在线处理,怎么用考虑顺序问题呢?我们对于每一个点,我们只有在用到它的时候才会对他进行pushdown操作,这就会导致在对一个点进行pushdown
操作之前,这个点上可能就会有很多个标记,这里说的就是在一个点上既有乘法标记又有加法标记的时候的处理顺序。
为了下面叙述方便,我现在声明此题是要先乘再加。为什么呢?看下面这个例子:
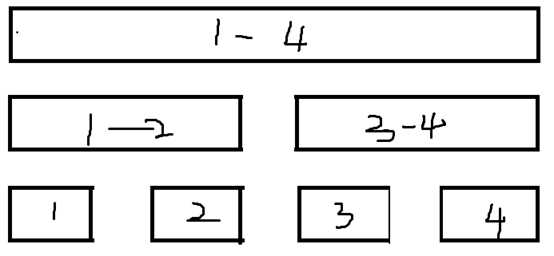
假设我们有一颗初始状态如上图所示的线段树,我们假设这个线段树1~2这个区间有两个标记(即加法和乘法标记都有值),并且我们暂且将这个节点维护的区间的值定为sum,把它的乘法标记的值
暂定为mul,把它的加法标记的值暂定为add。
在先乘再加的顺序下,sum的值会被更新为:sum=(summul+add(r-l+1))%p。
这里r-l+1即为该节点所维护的区间的区间长度。很显然,这样写并没有什么问题。但是,如果我们先加再乘呢?
先加再乘的话,我们就可以得到:sum=((sum+add)*mul)%p。这个式子看起来人畜无害,但是这个式子极其难以进行更新,只要我们改变一下add的值,mul就可能变成各种奇奇怪怪的无限循
环小数(因为在这个式子里add和mul是互相关联的),而我们用的又是整型变量,所以就会出现各种精度丢失问题,导致整个代码炸掉。
剩下的细节和实现问题就看代码吧。
Code
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#define MAXN 100010
#define INF 0x3f3f3f3f
typedef long long ll;
int n,m,p;
ll a[MAXN];
struct node{
ll val;
ll add, mul;
} tree[MAXN << 2];
//结构体数组,存储树状数组每项的值和lazytag的值
inline int lson(int k) { return k << 1; };//求左儿子
inline int rson(int k) { return k << 1 | 1; };//求右儿子
inline void push_up(int k){//pushup的时候千万不要忘了取模
tree[k].val = (tree[lson(k)].val + tree[rson(k)].val) % p;
return;
}
inline void push_down(int k,int l,int r){//重要的pushdown操作,注意一定要先乘后加
int mid = (l + r) >> 1;
tree[lson(k)].val = (tree[lson(k)].val * tree[k].mul + tree[k].add * (mid - l + 1)) % p;
tree[rson(k)].val = (tree[rson(k)].val * tree[k].mul + tree[k].add * (r - mid)) % p;
//不要忘了先乘后加!!!
tree[lson(k)].mul = (tree[lson(k)].mul * tree[k].mul) % p;//更新乘法标记
tree[rson(k)].mul = (tree[rson(k)].mul * tree[k].mul) % p;//……
tree[lson(k)].add = (tree[lson(k)].add * tree[k].mul + tree[k].add) % p;//更新加法标记
tree[rson(k)].add = (tree[rson(k)].add * tree[k].mul + tree[k].add) % p;//……
tree[k].add = 0;//清空加法标记
tree[k].mul = 1;//清空乘法标记,一定要赋值为1,否则怎么乘都是0
return;
}
void build(int k,int l,int r){
tree[k].add = 0;//加法标记赋值为0
tree[k].mul = 1;//乘法标记一定要为1
if(l==r){//若遍历到叶子结点,直接赋值
tree[k].val = a[l];
return;
}
int mid = (l + r) >> 1;
build(lson(k), l, mid);//建立左子树
build(rson(k), mid + 1, r);//建立右子树
push_up(k);//上传
}
void update_add(int k,int cl,int cr,int l,int r,ll v){//更新加法
if(cl<=l&&r<=cr){//若当前区间被更新区间完全包括,直接更新
tree[k].val = (tree[k].val + v * (r - l + 1)) % p;//更新标记
tree[k].add = (tree[k].add + v) % p;//只更新当前节点的值
return;
}
push_down(k, l, r);//下放标记
int mid = (l + r) >> 1;
if(cl<=mid)//若更新区间有一部分在左儿子,更新左儿子
update_add(lson(k), cl, cr, l, mid, v);
if(cr>mid)//若更新区间有一部分在右儿子,更新右儿子
update_add(rson(k), cl, cr, mid + 1, r, v);
push_up(k);//上传
}
void update_mul(int k,int cl,int cr,int l,int r,ll v){
if(cl<=l&&r<=cr){//若当前区间被更新区间完全包括,直接更新
tree[k].val = (tree[k].val * v) % p;
tree[k].mul = (tree[k].mul * v) % p;
tree[k].add = (tree[k].add * v) % p;
return;//……同上
}
push_down(k, l, r);//下放标记
int mid = (l + r) >> 1;
if(cl<=mid)//若更新区间有一部分在左儿子,更新左儿子
update_mul(lson(k), cl, cr, l, mid, v);
if(cr>mid)//若更新区间有一部分在右儿子,更新右儿子
update_mul(rson(k), cl, cr, mid + 1, r, v);
push_up(k);//上传
}
ll query(int k,int ql,int qr,int l,int r){
ll res = 0;
if(ql<=l&&r<=qr)//若查询区间有一部分在左儿子,直接返回当前区间的值
return tree[k].val;
push_down(k, l, r);//下放标记
int mid = (l + r) >> 1;
if(ql<=mid)//若查询区间有一部分在左儿子,查询左儿子
res = (res + query(lson(k), ql, qr, l, mid)) % p;
if(qr>mid)//若查询区间有一部分在右儿子,更新右儿子
res = (res + query(rson(k), ql, qr, mid + 1, r)) % p;
return res;//返回结果
}
int main(){
scanf("%d%d", &n, &m);
scanf("%d", &p);
for (int i = 1; i <= n;++i)
scanf("%lld", &a[i]);
//读入……
build(1, 1, n);//建树……
for (int i = 1; i <= m;++i){
int opt=0;
int x = 0, y = 0;
scanf("%d", &opt);
scanf("%d%d", &x, &y);
//读入……
if(opt==1){
ll k = 0;
scanf("%lld", &k);
update_mul(1, x, y, 1, n, k);
//乘法更新
}
if(opt==2){
ll k = 0;
scanf("%lld", &k);
update_add(1, x, y, 1, n, k);
//加法更新
}
if(opt==3)//查询
printf("%lld\n", query(1, x, y, 1, n));
}
return 0;
}
标签:返回 返回结果 cpp 难度 clu 题目 导致 date 就会
原文地址:https://www.cnblogs.com/ShadowFlowhyc/p/13381784.html