Luogu P3275 [SCOI2011]糖果

标签：bool   std   inf   clu   etc   string   getch   图片   pos   

思路

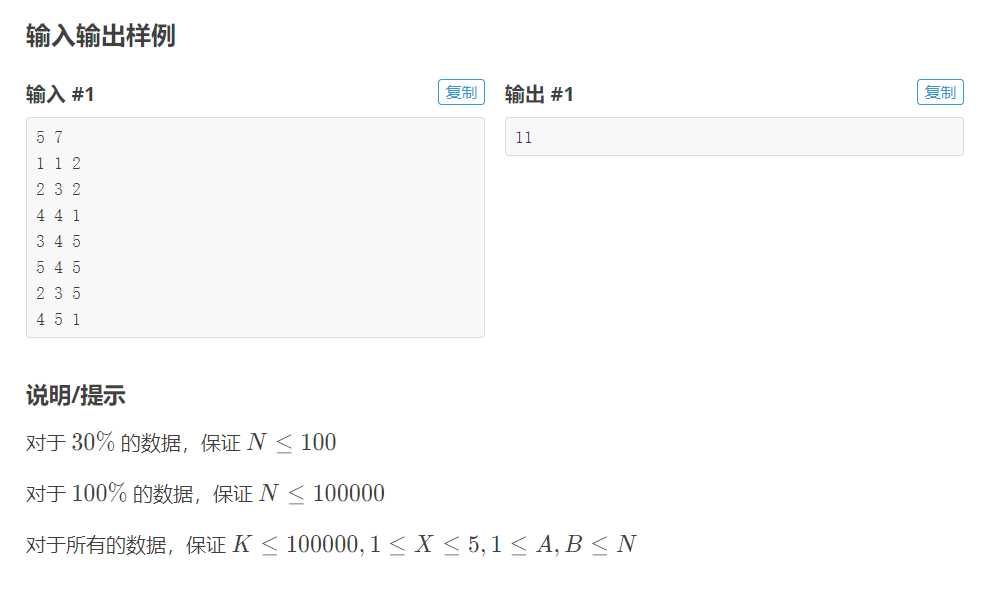
这个题是近似于差分约束的模板题（稍微难一点点），差分约束我之前好像听yt神仙讲过。

不懂差分约束的自行百度。

这个题需要注意的就是在建立超级原点的时候要倒叙建边（理论上正倒序都可以，但是这个题正序过不了应该是数据造得比较奇特）。

update：2020.7.26 正序这个题是可以正常过的，个人认为能不能过取决于代码效率

然后再就是套个差分约束板子就行，注意有负环时无解，而且每个点至少有一个糖果。

//这个题也可以用tarjan缩点+toposort做（题解里看到的），但是相较于差分约束那玩意难写得多，所以就没写那种做法QWQ。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#define INF 0x3f3f3f3f
#define MAXN 100010
typedef long long ll;
int n, k;
int head[MAXN], cnt;
int dis[MAXN], used[MAXN];
bool flag[MAXN];
struct node{
    int nxt, to;
    int val;
} edge[MAXN << 1];
inline int read(void){
    int f = 1, x = 0;char ch;
    do{ch = getchar();if(ch==‘-‘)f = -1;} while (ch < ‘0‘ || ch > ‘9‘);
    do{ x = (x << 1) +(x << 3) + ch - ‘0‘;ch = getchar();} while (ch >= ‘0‘ && ch <= ‘9‘);
    return f * x;
}
inline void add_edge(int x,int y,int z){
    ++cnt;
    edge[cnt].nxt = head[x];
    edge[cnt].to = y;
    edge[cnt].val = z;
    head[x] = cnt;
    return;
}
void _init(void){
    for (int i = 0; i <= n;++i)
        dis[i] = -INF, flag[i] = 0, used[i] = 1;
    return;
}
ll SPFA(void){
    std::queue<int> Q;
    Q.push(0), flag[0] = 1;
    dis[0] = 0;
    while(!Q.empty()){
        int u = Q.front();
        Q.pop(), flag[u] = 0;
        if(used[u]>=n) return -1;
        for (int i = head[u]; i;i=edge[i].nxt){
            int v = edge[i].to;
            if(dis[u]+edge[i].val>dis[v]){
                dis[v] = dis[u] + edge[i].val;
                ++used[u];
                if(!flag[v])
                    Q.push(v), flag[v] = 1;
            }
        }
    }
    ll res = 0;
    for (int i = 1; i <= n;++i)
        res += dis[i];
    return res;
}
int main(){
    n=read(),k=read();
    for (int i = 1; i <= k;++i){
        int x = read();
        int a = read(), b = read();
        if(!(x&1)&&a==b){puts("-1");return 0;}
        if(x==1) add_edge(a, b, 0), add_edge(b, a, 0);
        if(x==2) add_edge(a, b, 1);
        if(x==3) add_edge(b, a, 0);
        if(x==4) add_edge(b, a, 1);
        if(x==5) add_edge(a, b, 0);
    }
    for (int i = n; i >= 1;--i)
        add_edge(0, i, 1);
    _init();
    printf("%lld\n", SPFA());
    return 0;
}

Luogu P3275 [SCOI2011]糖果

标签：bool   std   inf   clu   etc   string   getch   图片   pos   

原文地址：https://www.cnblogs.com/ShadowFlowhyc/p/13381711.html