标签:obj incr not 技术 inf etc src nbsp 动态规划
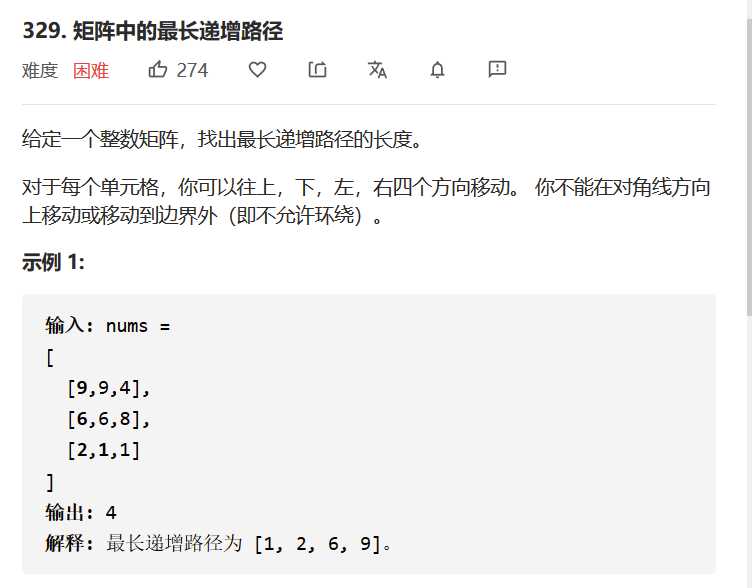
题目描述:

方法一:动态规划 O(mnlogmn)
class Solution(object): def longestIncreasingPath(self, matrix): if not matrix or not matrix[0]: return 0 m, n = len(matrix), len(matrix[0]) lst = [] for i in range(m): for j in range(n): lst.append((matrix[i][j], i, j)) lst.sort() dp = [[0 for _ in range(n)] for _ in range(m)] for num, i, j in lst: dp[i][j] = 1 for di, dj in [(0, 1), (1, 0), (0, -1), (-1, 0)]: r, c = i + di, j + dj if 0 <= r < m and 0 <= c < n: if matrix[i][j] > matrix[r][c]: dp[i][j] = max(dp[i][j], 1 + dp[r][c]) return max([dp[i][j] for i in range(m) for j in range(n)])
方法二:记忆化深搜 O(mn) O(mn)
class Solution(object): def longestIncreasingPath(self, matrix): if not matrix or not matrix[0]: return 0 dirs = [(0,-1),(0,1),(1,0),(-1,0)] rows,columns = len(matrix),len(matrix[0]) @lru_cache(None) def helper(row,column): best = 1 for _i,_j in dirs: newrow,newcolumn = row + _i,column + _j if 0 <= newrow < rows and 0 <= newcolumn < columns and matrix[row][column] < matrix[newrow][newcolumn]: best = max(best,helper(newrow,newcolumn) + 1) return best ans = 0 for i in range(rows): for j in range(columns): ans = max(ans,helper(i,j)) return ans
标签:obj incr not 技术 inf etc src nbsp 动态规划
原文地址:https://www.cnblogs.com/oldby/p/13384749.html