Luogu P5603 小C与桌游

标签：lin   lazy   algorithm   贪心   define   code   priority   return   lan   

思路

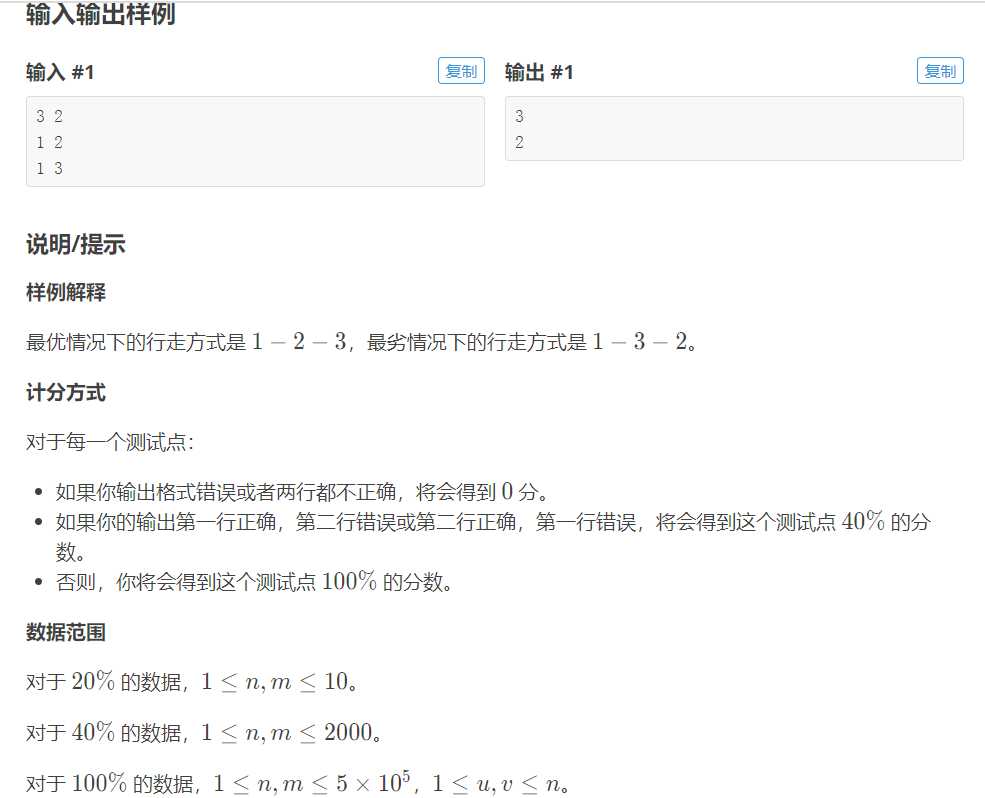
这个题一看和入度扯上关系就是明显的topo了。

对于最优情况，直接维护小根堆，贪心即可。

对于最劣情况，显然直接维护大根堆然后贪心是错误的（反例见Luogu题解），所以每次要取出所有能拓展的节点，依次加入队列topo即可。这里注意当连到的点比当前最大值大时，压入大根堆，

否则加入队列。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#define MAXN 500010
std::priority_queue<int> Q1;
std::priority_queue<int> Q2;
int n, m, res1, res2;
int head[MAXN], cnt;
int in1[MAXN], in2[MAXN];
struct node{
    int nxt, to;
} edge[MAXN];
class Queue{
    private:
        int q[MAXN << 1];
        int head, tail;
    public:
        inline void Push(int x) { q[++tail] = x; return; }
        inline int Front(void) { return q[head + 1]; }
        inline void Pop(void) { ++head; return; }
        inline bool Empty(void) { return head == tail ? true : false; }
} Q;
inline int read(void){
    int f = 1, x = 0;char ch;
    do{ch = getchar();if(ch==‘-‘)f = -1;} while (ch < ‘0‘ || ch > ‘9‘);
    do{ x = (x << 1) + (x << 3) + ch - ‘0‘;ch = getchar();} while (ch >= ‘0‘ && ch <= ‘9‘);
    return f * x;
}
inline int _max(int x, int y) { return x > y ? x : y; }
inline void add_edge(int x,int y){
    ++cnt;
    edge[cnt].nxt = head[x];
    edge[cnt].to = y;
    head[x] = cnt;
    return;
}
void toposort1(void){
    int maxx = 0;
    while(!Q1.empty()){
        int u = -Q1.top();
        Q1.pop();
        if(u>maxx) ++res1;
        maxx = _max(maxx, u);
        for (int i = head[u]; i;i=edge[i].nxt){
            int v = edge[i].to;
            --in1[v];
            if(!in1[v]) Q1.push(-v);
        }
    }
    return;
}
void toposort2(void){
    int maxx = 0;
    while(!Q2.empty()){
        int u = Q2.top();
        if(u>maxx) ++res2;
        while(!Q2.empty()){
            Q.Push(Q2.top());
            Q2.pop();
        }
        while(!Q.Empty()){
            int u1 = Q.Front();
            Q.Pop();
            maxx = _max(maxx, u1);
            for (int i = head[u1]; i;i=edge[i].nxt){
                int v1 = edge[i].to;
                --in2[v1];
                if(!in2[v1]){
                    if(v1>maxx) Q2.push(v1);
                    else Q.Push(v1);
                }
            }
        }
    }
    return;
}
int main(){
    n = read(), m = read();
    for (int i = 1; i <= m;++i){
        int u = read(), v = read();
        add_edge(u, v);
        ++in1[v], ++in2[v];
    }
    for (int i = 1; i <= n;++i)
        if(!in1[i]) Q1.push(-i), Q2.push(i);
    toposort1();
    toposort2();
    printf("%d\n%d\n", res1, res2);
    return 0;
}

Luogu P5603 小C与桌游

标签：lin   lazy   algorithm   贪心   define   code   priority   return   lan   

原文地址：https://www.cnblogs.com/ShadowFlowhyc/p/13389048.html