[编程题] nk：[二叉搜索树的后序遍历]

标签：root   传参   coder   图片   logs   存在   思想   http   方法   

[编程题] nk：二叉搜索树的后序遍历

输入输出

无

思路

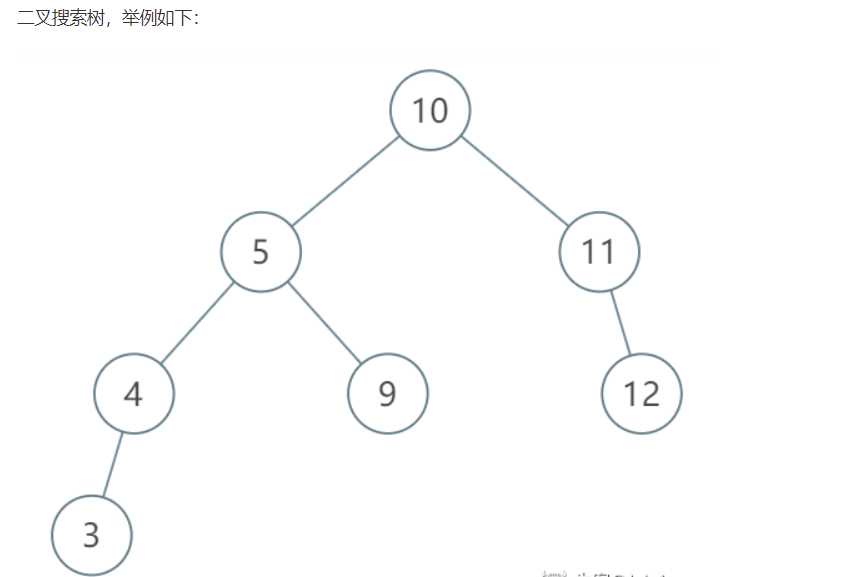
代码思路：

我们可以采用递归的思想，每次处理本次流程的时候（比如该组元素有n个），拿出最后一个节点当作是root节点，然后，在剩下的n-1 中，确定出前边的左子树部分都比root小，左子树后的右子树部分都比roo大；

比如：一开始调用传入的是solve(arr,left,right);

（1）此时，我们得到本次的root = arr[right];

? 指定一个用于比较指向的指针int i=0;

? 指定一个变量split 用于记录本次的分割点（分割左 右子树）

（2）在指针i从本次的数组的left处，一直判断，如果arr[i]<root ，就指针右移；当找到了arr[i]>root的时候，指针就是指向了右子树的部分的第一个元素了。 【这里也有可能就是指针走到了right-1的那个元素了，也没找到比root大的元素，就是仅有左子树，无右子树的情况，需要考虑进去，如果是仅有左子树无右子树，那就无分割，无需递归这组数据产生的左子树和右子树是否满足的了，直接返回true】

（3）此时继续让指针移动往后判断右子树情况。如果arr[i]>root，就正常i++后移。当到达了right-1的那个节点就是比较完了右子树，说明本次的左右部分都满足二叉树的情况。那接下来就是需要对本次这组数据分割的两部分子树进行上述逻辑判断了，如果也满足，那这组数据就返回true

• 当在右子树的判断过程中，如果出现了arr[i]<root的话（即右子树小于root的情况），直接返回false,本组数据肯定不满足二叉排序树。

Java代码（递归处理）

public class Solution {
    public boolean VerifySquenceOfBST(int [] sequence) {
       return  verify(sequence,0,sequence.length-1);
    }
    
    public boolean verify(int[] seq,int left,int right){
        //极端条件处理
        if(seq==null || seq.length==0) {return false;}
        
        //===================递归的退出条件===================
        if(left>=right){
            return true;
        }
        
        //===================递归的处理方法体=====================
        int root = seq[right];  //根永远都是子树的最右边的那个节点
        int i = left;  //用于元素比较的指针
        int split = 0; //标记大小分界点，用于递归传参
        
        //处理判断左子树，从头开始找，如果当前值小于root,指针右移
        while(i<right && seq[i]<root){
           i++;
        }
        
        //标记切割点（此时指针i指向了右子树的第一个大于root的节点）
        split = i;
        
        //判断右子树
        if(i>=right){
            //说明在上边的查找左子树的中已经走到头了，该次没有右子树，且左子树都小于root
            return true; //仅有左子树无右子树也无序递归了，直接返回这组数据满足
        }else{
            //如果还没到头，那就继续比较看是否都是大于root的节点
            while(i<right){
                if(seq[i]>root) {i++;}
                else{return false;}  //存在不满足的情况直接返回了false；
             }
        }
        //递归子树（正常退出了上述的while,那么就是此次满足，递归遍历该次分割的子树，两子树都满足则满足）
        return verify(seq,left,split-1) && verify(seq,split,right-1);
    }
}

输出：

[编程题] nk：[二叉搜索树的后序遍历]

标签：root   传参   coder   图片   logs   存在   思想   http   方法   

原文地址：https://www.cnblogs.com/jiyongjia/p/13391511.html