标签:near 签名 不同 big hold trying research index UNC

The task of finding nearest neighbours is very common. You can think of applications like finding duplicate or similar documents, audio/video search. Although using brute force to check for all possible combinations will give you the exact nearest neighbour but it’s not scalable at all. Approximate algorithms to accomplish this task has been an area of active research. Although these algorithms don’t guarantee to give you the exact answer, more often than not they’ll be provide a good approximation. These algorithms are faster and scalable.
Locality sensitive hashing (LSH) is one such algorithm. LSH has many applications, including:

In this blog, we’ll try to understand the workings of this algorithm.
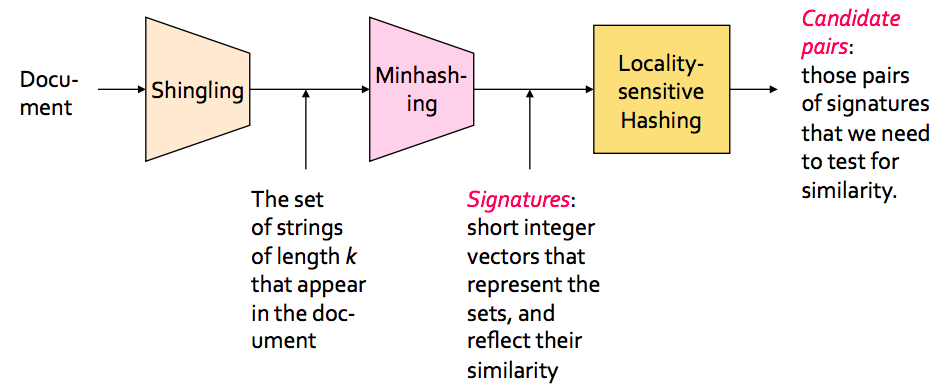
LSH refers to a family of functions (known as LSH families) to hash data points into buckets so that data points near each other are located in the same buckets with high probability, while data points far from each other are likely to be in different buckets. This makes it easier to identify observations with various degrees of similarity.
Let’s try to understand how we can leverage LSH in solving an actual problem. The problem that we’re trying to solve:
Goal: You have been given a large collections of documents. You want to find “near duplicate” pairs.
In the context of this problem//////再次问题的背景下, we can break down the LSH algorithm into 3 broad steps:
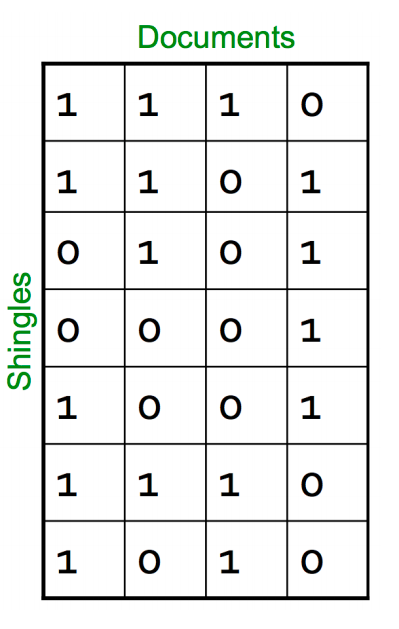
In this step, we convert each document into a set of characters of length k (also known as k-shingles or k-grams). The key idea is to represent each document in our collection as a set of k-shingles.
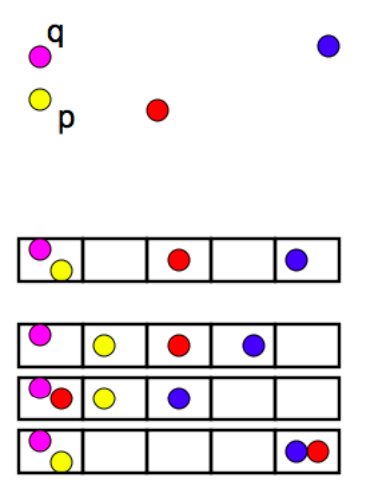
For ex: One of your document (D): “Nadal”. Now if we’re interested in 2-shingles, then our set: {Na, ad, da, al}. Similarly set of 3-shingles: {Nad, ada, dal}.
We’ve a representation of each document in the form of shingles. Now, we need a metric to measure similarity between documents. Jaccard Index is a good choice for this. Jaccard Index between document A & B can be defined as:
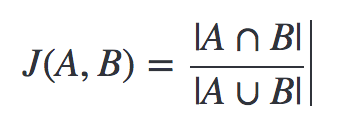
It’s also known as intersection over union (IOU).
A: {Na, ad, da, al} and B: {Na, ad, di, ia}.
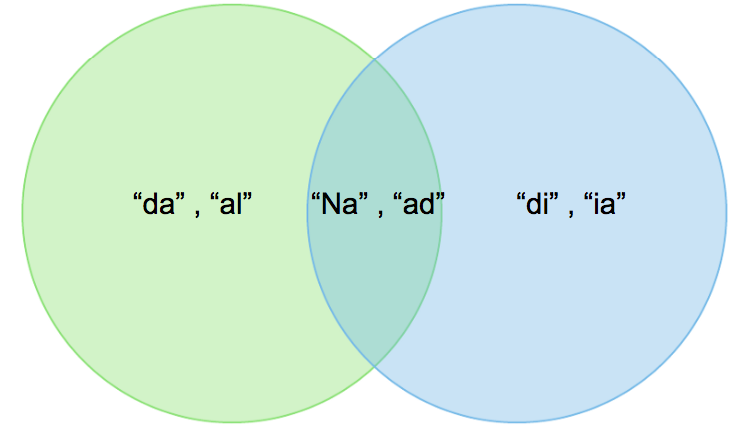
Jaccard Index = 2/6
Let’s discuss 2 big issues that we need to tackle:
Now you may be thinking that we can stop here. But if you think about the scalability, doing just this won’t work. For a collection of n documents, you need to do n*(n-1)/2 comparison, basically O(n2). Imagine you have 1 million documents, then the number of comparison will be 5*1011 (not scalable at all!).
The document matrix is a sparse matrix and storing it as it is will be a big memory overhead. One way to solve this is hashing.
The idea of hashing is to convert each document to a small signature using a hashing function H*.* Suppose a document in our corpus is denoted by d. Then:
Choice of hashing function is tightly linked to the similarity metric we’re using. For Jaccard similarity the appropriate hashing function is min-hashing.
This is the critical and the most magical aspect of this algorithm so pay attention:
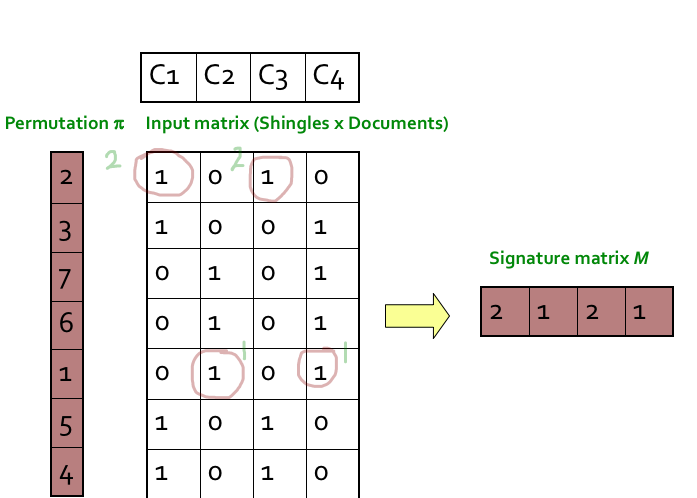
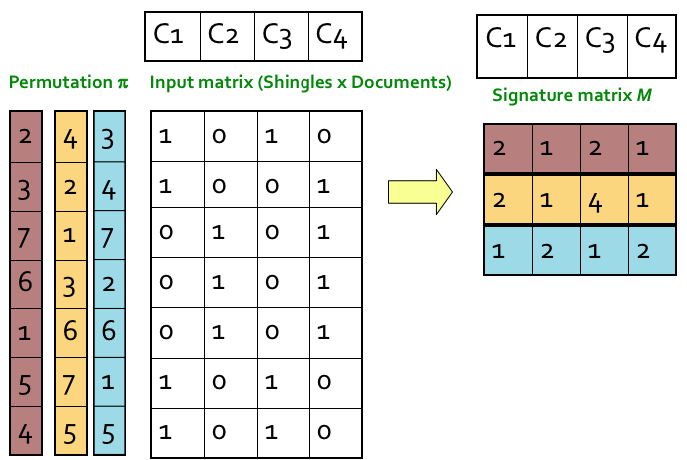
Step 1: Random permutation (π) of row index of document shingle matrix.

////////对行进行随机排列
Step 2: Hash function is the index of the first (in the permuted order) row in which column C has value 1. Do this several time (use different permutations) to create signature of a column.
第2步:哈希函数是列C值为1的第一行(按顺序排列)的索引。这样做几次(使用不同的排列)来创建一个列的签名。
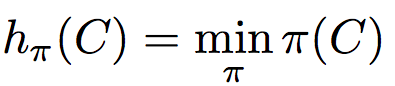
////这个图根本看不懂?? ////看了视频懂了
The similarity of the signatures is the fraction of the min-hash functions (rows) in which they agree. So the similarity of signature for C1 and C3 is 2/3 as 1st and 3rd row are same.
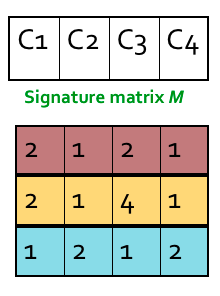
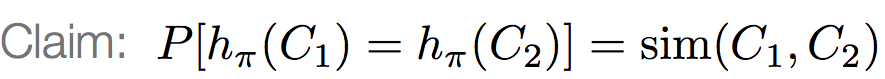
Expected similarity of two signatures is equal to the Jaccard similarity of the columns. The longer the signatures, the lower the error.
In the below example you can see this to some extent. There is difference as we have signatures of length 3 only. But if increase the length the 2 similarities will be closer.
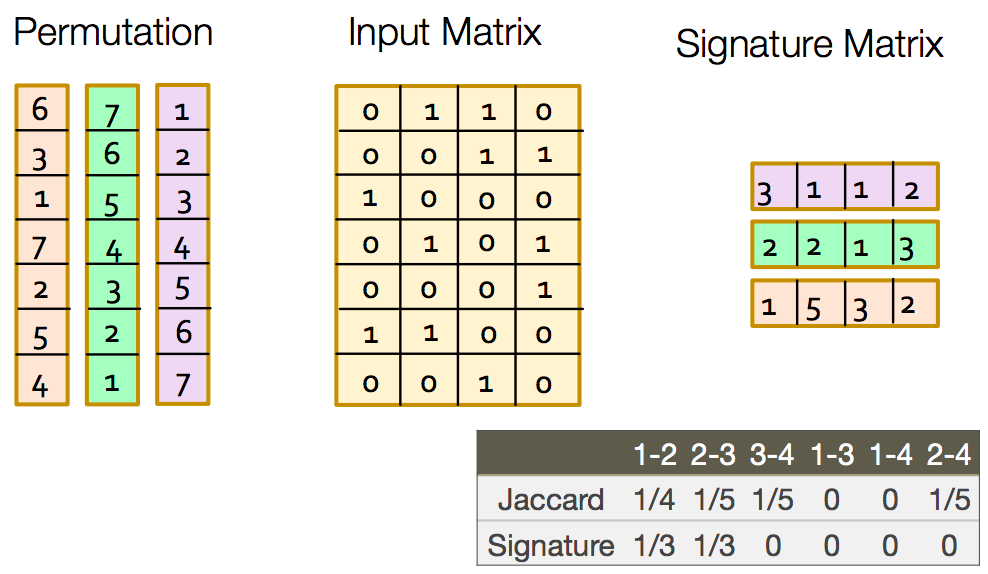
So using min-hashing we have solved the problem of space complexity by eliminating the sparseness and at the same time preserving the similarity. In actual implementation their is a trick to create permutations of indices which I’ll not cover but you can check this video around 15:52. Min-hash implementation
Goal: Find documents with Jaccard similarity of at least t
The general idea of LSH is to find a algorithm such that if we input signatures of 2 documents, it tells us that those 2 documents form a candidate pair or not i.e. their similarity is greater than a threshold t. Remember that we are taking similarity of signatures as a proxy for Jaccard similarity between the original documents.
Specifically for min-hash signature matrix:
Now the question is how to create different hash functions. For this we do band partition.
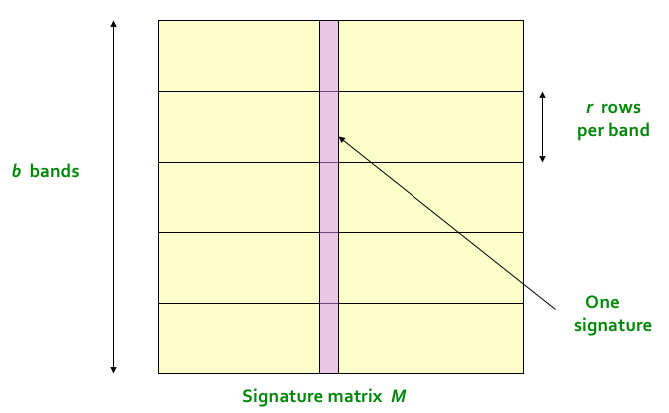
Here is the algorithm:
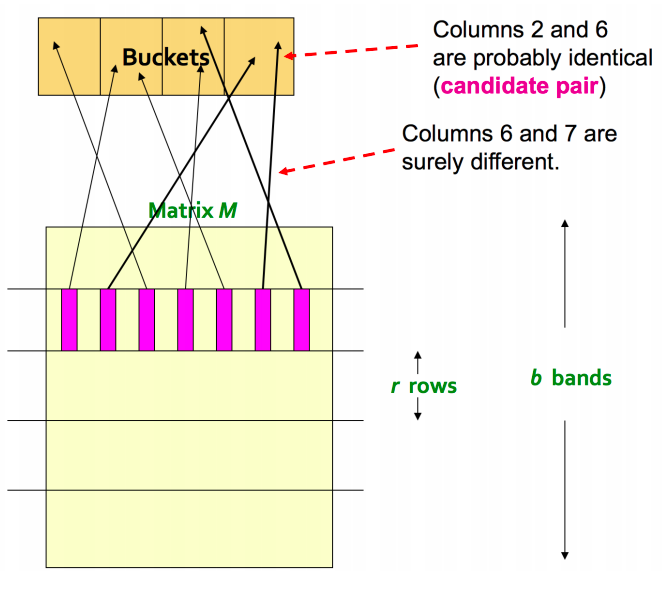
Divide the signature matrix into b bands, each band having r rows
For each band, hash its portion of each column to a hash table with k buckets
Candidate column pairs are those that hash to the same bucket for at least 1 band
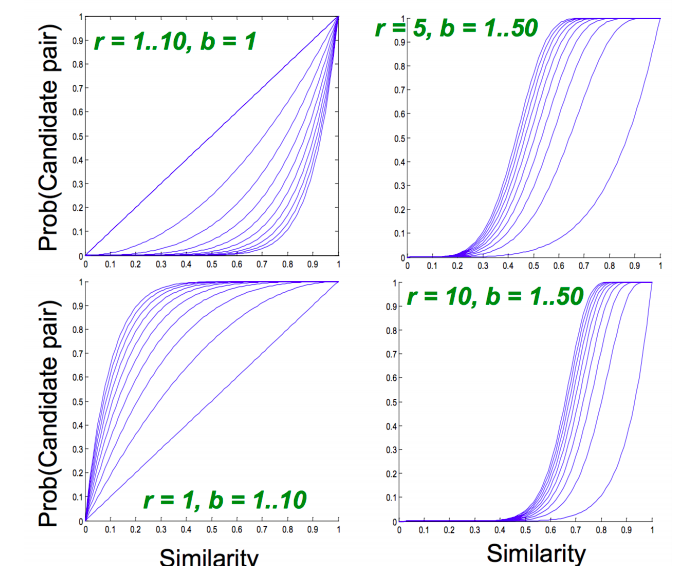
Tune b and r to catch most similar pairs but few non similar pairs
There are few considerations here. Ideally for each band we want to take k to be equal to all possible combinations of values that a column can take within a band. This will be equivalent to identity matching. But in this way k will be a huge number which is computationally infeasible. For ex: If for a band we have 5 rows in it. Now if the elements in the signature are 32 bit integers then k in this case will be (232)? ~ 1.4615016e+48. You can see what’s the problem here. Normally k is taken around 1 million.////没看明白
The idea is that if 2 documents are similar then they will will appear as candidate pair in at least one of the bands.
If we take b large i.e more number of hash functions, then we reduce r as b*r is a constant (number of rows in signature matrix). Intuitively it means that we’re increasing the probability of finding a candidate pair. This case is equivalent to taking a small t (similarity threshold)
Let’s say your signature matrix has 100 rows. Consider 2 cases:
Let’s say your signature matrix has 100 rows. Consider 2 cases:
b1 = 10 → r = 10
b2 = 20 → r = 5
In 2nd case, there is higher chance for 2 documents to appear in same bucket at least once as they have more opportunities (20 vs 10) and fewer elements of the signature are getting compared (5 vs 10).
Higher b implies lower similarity threshold (higher false positives) and lower b implies higher similarity threshold (higher false negatives)
Let’s try to understand this through an example.
00k documents stored as signature of length 100
Signature matrix: 100*100000
Brute force comparison of signatures will result in 100C2 comparisons = 5 billion (quite a lot!)
Let’s take b = 20 → r = 5
similarity threshold (t) : 80%
We want 2 documents (D1 & D2) with 80% similarity to be hashed in the same bucket for at least one of the 20 bands.
P(D1 & D2 identical in a particular band) = (0.8)? = 0.328
P(D1 & D2 are not similar in all 20 bands) = (1–0.328)^20 = 0.00035
Also we want 2 documents (D3 & D4) with 30% similarity to be not hashed in the same bucket for any of the 20 bands (threshold = 80%).
P(D3 & D4 identical in a particular band) = (0.3)? = 0.00243
P(D3 & D4 are similar in at least one of the 20 bands) = 1 — (1–0.00243)^20 = 0.0474
This means in this scenario we have ~4.74% chance of a false positive @ 30% similar documents.
So we can see that we have some false positives and few false negatives. These proportion will vary with choice of b and r.
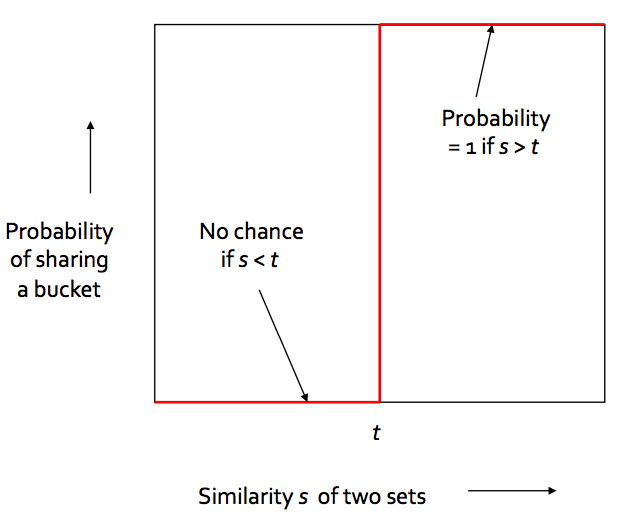
Worst case will be if we have b = number of rows in signature matrix as shown below.
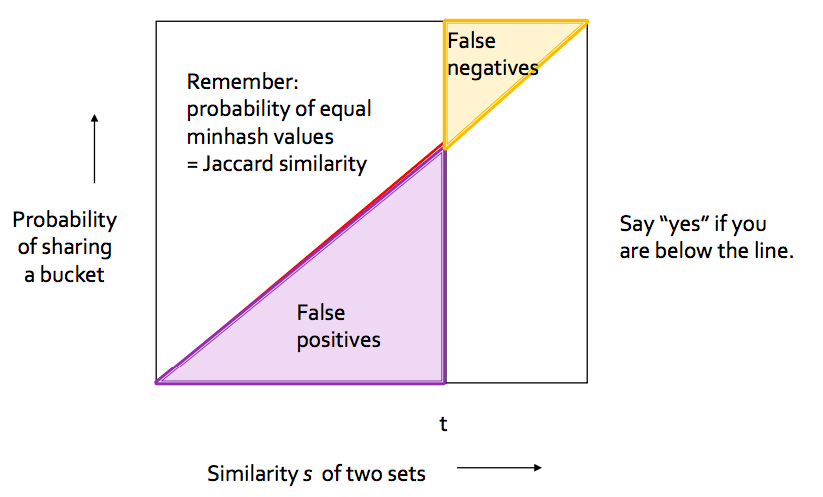
Generalised case for any b and r is shown below.
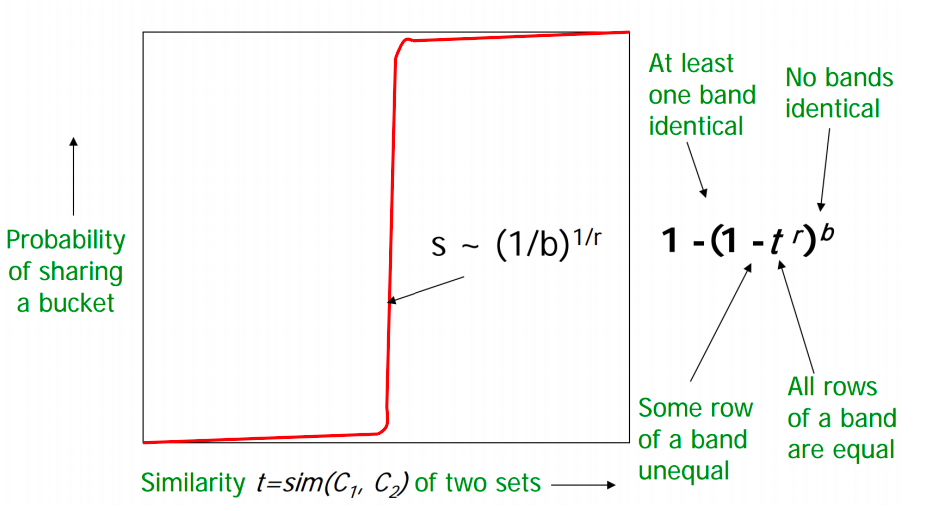
Choose b and r to get the best S-curve i.e minimum false negative and false positive rate
I hope that you have a good understanding of this powerful algorithm and how it reduces the search time. You can imagine how LSH can be applicable to literally any kind of data and how much it’s relevant in today’s world of big data.
To read more on the code implementation of LSH, checkout this article. https://santhoshhari.github.io/Locality-Sensitive-Hashing/
转自:
标签:near 签名 不同 big hold trying research index UNC
原文地址:https://www.cnblogs.com/xiaofeisnote/p/13394446.html