标签:初始 作用 特征 复杂 决策树 保留 计算机视觉 需要 相同
激活函数:增加非线性
??如果不用激活函数,每一层节点的输入都是上层输出的线性函数。无论神经网络有多少层,输出都是输入的线性组合,与没有隐藏层效果相当,因此网络的逼近能力就相当有限。
Sigmoid:
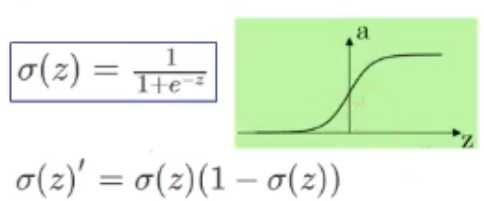
??将输入的连续实值变换为0-1的输出。反向传播中易发生梯度消失,输出不对称(只输出正值)
tanh:
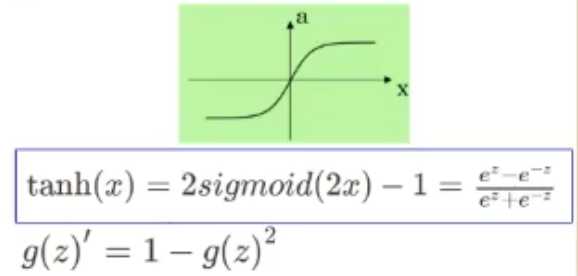
??输出为-1 - 1
relu:
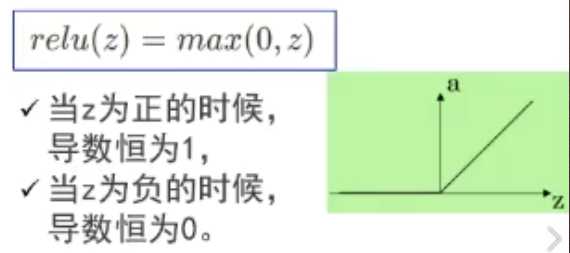
??计算速度快,只需判断输入是否大于0。某些神经元可能永远不会被激活,导致相应的参数永远不能被更新
??常用
?
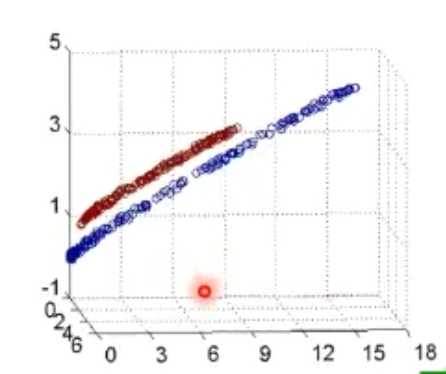
线性分类任务组合后可以解决非线性分类任务
前几层感知器理解为空间的变换,将非线性问题变为线性问题
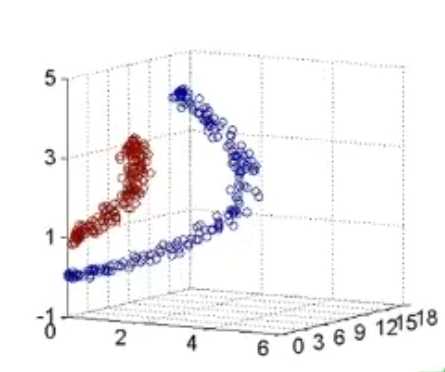
?
增加节点数:增加维度,即增加线性转换能力
增加层数:增加激活函数次数,即增加非线性转换次数
?
残差:损失函数在某个结点的偏导?? \(da^{[1]}=\frac{\partial L}{\partial a^{[1]}}=\frac{\partial L}{\partial z^{[2]}}\cdot W^{[2]}\)
?
BP反向传播
??前馈??\(z^{[2]}=W^{[2]}\cdot a^{[1]}\)
??反馈??\(da^{[1]}=W^{[2]}\cdot dz^{[2]}\rightarrow\frac{\partial L}{\partial W^{[1]}}=dz^{[1]}\cdot x\)??复合求导
??(1)先计算每一层的状态和激活值,直到最后一层(前向传播)
??(2)计算每一层的误差,误差计算过程是从最后一层向前推进(反向传播)
??(3)更新参数
?
梯度消失
??接近输入层的参数更新缓慢或停滞,此时的神经网络学习就等价于只有后面几层的隐藏层网络在学习。如sigmoid函数,求导结果是两个0-1的数相乘
??解决:
????使用深度信念网络(DBN),对每层神经元单独进行训练。
????使用其他激活函数,如relu
????使用长短期记忆(LSTM)单元和相关门类型的神经元结构
?
逐层预训练:先用无监督学习对每一层进行预训练,然后使用经过预训练的权值参数作为初始参数进行训练
??解决局部最小值,梯度消失
??自编码器:假设输入输出相同,先编码再解码
????两套编码函数
??受限玻尔兹曼机(两层,可见层,隐藏层)
????不同层全连接,层内无连接(二分图)
????共享权重矩阵W,两个偏置向量
?
矩阵线性变换
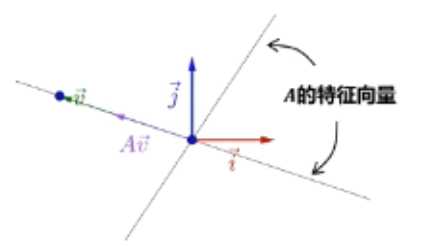
??矩阵相乘对原始向量同时施加方向变化和尺度变化
??对某些特殊向量(特征向量),矩阵的作用只有尺度变化而没有方向变化
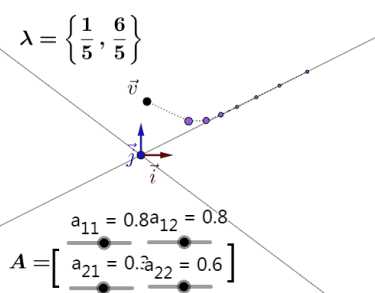
??任意向量v乘矩阵A次数足够多,会落到最大特征值的特征向量上(矩阵A和向量v相乘时,会把向量v向最大特征值对应的特征向量上引导)
?
秩
??线性方程组角度:度量矩阵行列之间的相关性
??数据点分布角度:数据需要的最小的基的数量
????数据分布模式越容易被捕捉,即需要的基越少,秩就越小
????数据冗余度越大,需要的基就越少,秩越小
????若矩阵表达的是结构化信息,如图像,用户-物品表等,各行之间存在一定相关性,一般是低秩的
?
低秩近似
??保留决定数据分布的最主要的模式/方向(丢弃的可能是噪声或其他不关键信息)
?
训练误差->泛化误差(测量的误差结果不一定真实反映真实情况)
??泛化误差(期望风险)
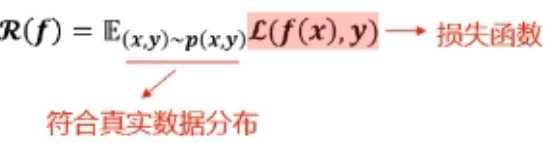
??训练误差(经验风险)
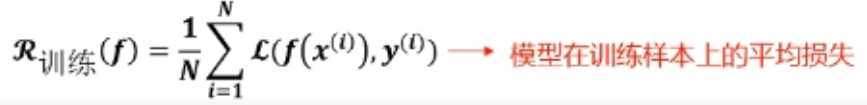

?
欠拟合:
??提高模型复杂度
????决策树:拓展分支
????神经网络:增加训练轮数
过拟合:
??降低模型复杂度
????优化目标加正则项
????决策树:剪枝
????神经网络:early stop,dropout
??数据增广
????计算机视觉:图像旋转,缩放,剪切
????自然语言处理:同义词替换
????语音识别:添加随机噪声
?
交叉熵(对数损失函数)替代平方损失
??信息量:一个事件发生的概率越大,则它所携带的信息量就越小,而当p(x0)=1时,熵将等于0,也就是说该事件的发生不会导致任何信息量的增加。
??信息熵:当一种信息出现概率更高的时候,表明它被传播得更广泛,或者被引用的程度更高。从信息传播的角度来看,信息熵可以表示信息的价值。
??交叉熵:心中的概率分布与实际的概率分布相差有多远。用这样的一个量,来定义预估事情的错误程度(loss)。
标签:初始 作用 特征 复杂 决策树 保留 计算机视觉 需要 相同
原文地址:https://www.cnblogs.com/Arsene-W/p/13409307.html