标签:问题 智能扫地机器人 规划 自动 高达 价格 生活 2016年 弯道超车
请从字符串中找出一个最长的不包含重复字符的子字符串,计算该最长子字符串的长度。 示例 1: 输入: "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。 示例 2: 输入: "bbbbb" 输出: 1 解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。 示例 3: 输入: "pwwkew" 输出: 3 解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。 请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
首先可以用动态规划求解此题。设动态规划表dp,dp[j]是以s[j]为结尾的“最长不重复字符串”的长度。dp[j-1]是第j-1个“最长不重复字符串”的长度。假设s[j]上一次出现的字符位置为i,则s[i]和s[j]之间的距离d=j-1,此时,dp[j-1]存在两种情况:
1.d>dp[j-1],想想这个距离大于dp[j-1],那么说明s[i]不在以s[j-1]为结尾的“最长不重复字符串”里面,此时dp[j]=dp[j-1]+1
2.d<=dp[j-1],说明s[i]在在以s[j-1]为结尾的“最长不重复字符串”里面,此时dp[j] = j -i。
此外,可以用一个hash map保存s[j]出现的位置, 如果重复出现,则更新为最近的位置,hash map的时间复杂度为O(1)。
再梳理一下动态规划的转移方程:
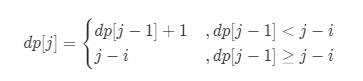
此时返回时max的最长不重复字符串。
代码:
class Solution: ‘‘‘ hash表+动态规划 ‘‘‘ def lengthOfLongestSubstring(self, s: str) -> int: dp = [] res = tmp = 0 dic = {} for j in range(len(s)): i = dic.get(s[j], -1) dic[s[j]] = j # tmp = tmp + 1 if tmp < j-i else j - i if j -i <= tmp: tmp = j -i elif j -i > tmp: tmp += 1 res = max(res, tmp) return res
这道题,其实最容易想到的就是时间复杂度为O(N^2)的双指针。类似滑动窗口的思想,用指针p1和p2指向字符串头,用一个滑动窗口始终维护当前不重复的最大长度的字符串s[p1:p2+1],当s[p2]不在这个字符串中,则从左向右移动p2,否则,从左向右移动p1,同时每次保存最大s[p1:p2+1]的长度,保存每次更新的最大值。
但是呢,这样时间复杂度高啊,p1和p2最差的情况需要O(N^2)。
class Solution: ‘‘‘ 滑动窗口+双指针 ‘‘‘ def lengthOfLongestSubstring(self, s: str) -> int: p1, p2= 0,0 res = 0 while p1 < len(s) and p2 < len(s): if s[p2] not in s[p1:p2]: res = max(res, p2+1 - p1) p2 += 1 else: p1 += 1 return res
因此如果我们在p2遇到重复的s[p2]时,直接将s[p1]指向前一个s[p2]出现的位置,(为什么要这么做呢?因此p1原来的位置到前一个s[p2]出现的位置这段位置已经包含了重复的s[p2],因此遍历这部分是没有意义的,最大字符串一定是在没有重复的)。这样的话,我们可以用一个hash表保存s[p2]的位置,如果下一次遇到s[p2]时,则将p1的指向s[p2]出现的前一个位置。
最大字符串长度则为每次的p2-p1的最大值。
此时时间复杂度O(N),空间复杂度O(N).
代码中i表示p1,j表示p2.
class Solution: ‘‘‘ hash表+双指针 ‘‘‘ def lengthOfLongestSubstring(self, s: str) -> int: res, i , Map =0, -1, {} for j in range(len(s)): if s[j] in Map: i = max(Map[s[j]], i) #求i的新位置 Map[s[j]] = j #哈希表记录s[j]的索引j res = max(res, j - i) return res
标签:问题 智能扫地机器人 规划 自动 高达 价格 生活 2016年 弯道超车
原文地址:https://blog.51cto.com/14869228/2518137