标签:大于 子节点 timer 变化 介绍 tree 基础 img xtend
上一章我们介绍了二叉树,二叉搜索树相关的一些知识。
当一个二叉搜索树是一个满二叉树,或者是完美二叉树的时候可以计算一下二叉搜索树的查找,插入,删除的时间复杂度。
从代码来看它们的时间复杂度都是和树的高度相关的。
满二叉树的高度是$log_2(n + 1)$,完美二叉树的高度是$floor(log_2n) +1$,所以当二叉树是满二叉树或者是完美二叉树的时候,树的高度接近 $logn$,所以插入、删除、查找操作的时间复杂度也比较稳定,是 $O(logn)$。
这是在满二叉树或者是完美二叉树的情况下,当插入、或者删除操作一些节点后,二叉搜索树可能会变成链表,也就是高度是 $n$的情况,这个时候插入,删除,查找的时间复杂度就变成了$O(n)$。
所以可以发现当 $n$ 比较大的时候最好和最坏的情况下时间复杂度相差很大
为了更高效的使用二叉搜索树,避免二叉搜索树退化成链表,就需要在二叉搜索树的添加,删除的时候尽量保持二叉搜索树的平衡。
平衡:当节点数固定的时候,左右子树的高度越接近,这颗二叉搜索树越平衡
最理想的情况当然就是满二叉树或者完美二叉树了,在相同节点数的情况下高度最低。
首先添加,删除的节点是随机的,无法控制,可以做的是在添加,或者删除动作后调整节点的位置,使得二叉树尽量保持平衡。
这种在添加,删除节点后仍然保持平衡二叉树叫自平衡二叉树
经典的自平衡二叉搜索树有
AVL 树是最早发明的自平衡二叉搜索树,取名于发明者的名字。
AVL 引入平衡因子的概念
某节点的左右子树的高度差
AVL 树的特点就是
下面是一组对比:二叉搜索树和 AVL 树插入相同数据后的表现
二叉搜索树
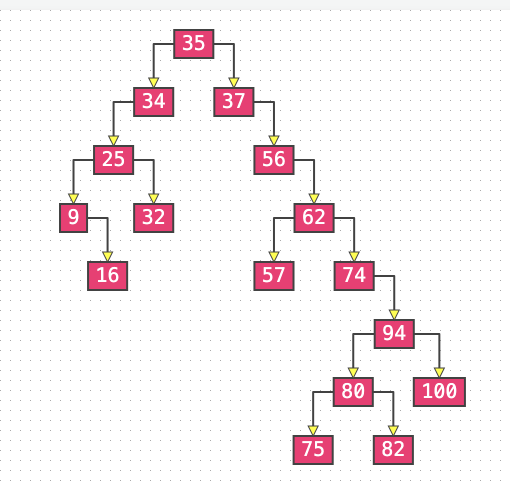
AVL 树
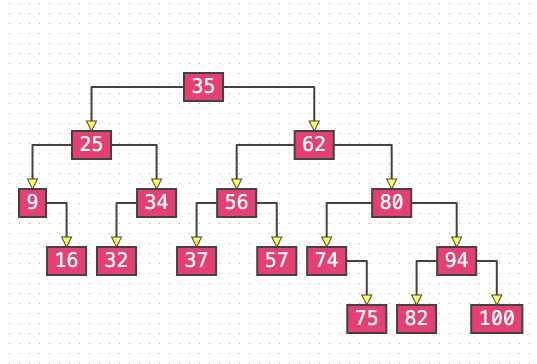
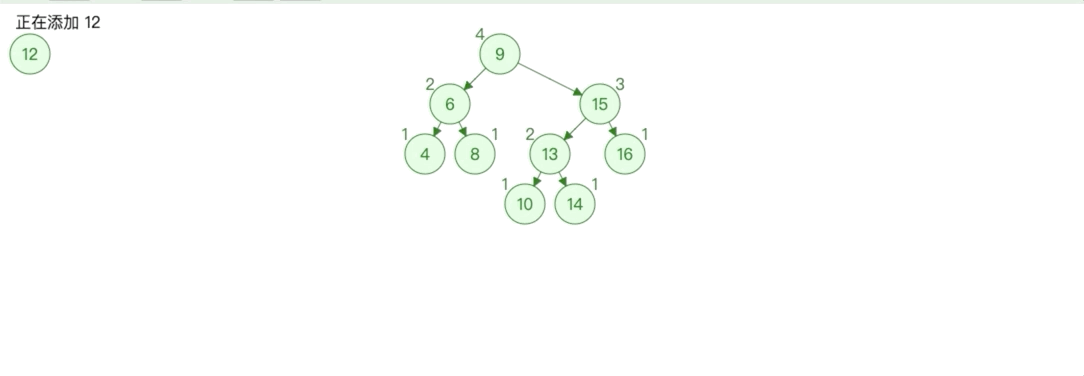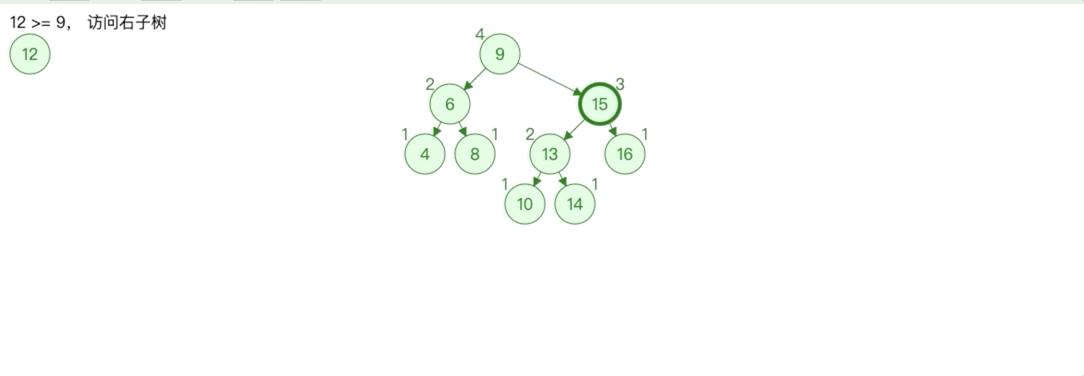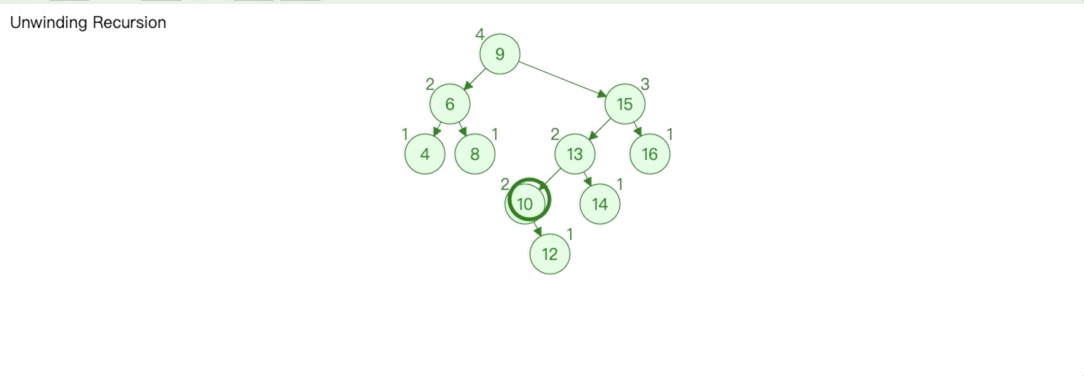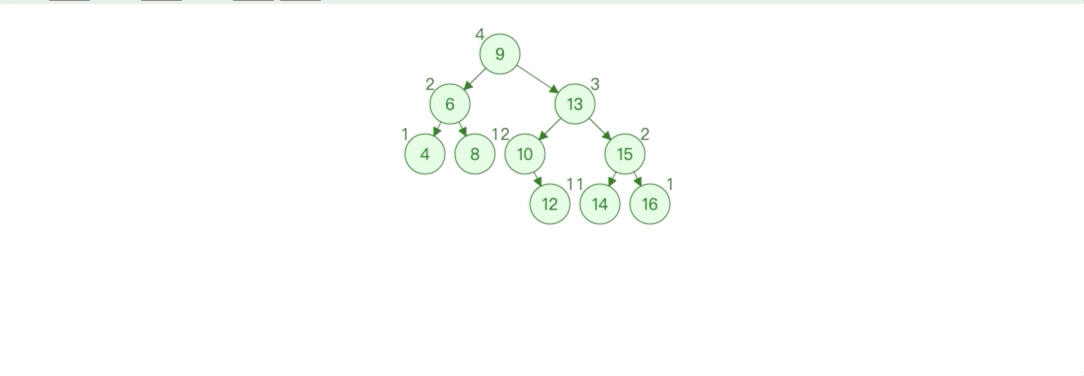
首先回忆一下二叉搜索树的添加,我们会从根节点开始一路向下比较,找到新添加节点的位置。所以因为添加而破坏树的平衡的的情况都会发生在叶子节点处,并且失衡只会发生在添加节点的祖先节点上,添加节点的父节点和非祖先节点都不会失衡。
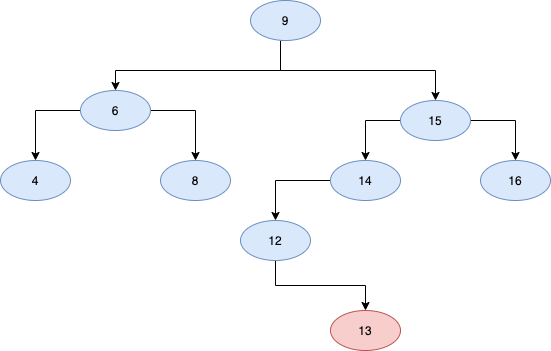
如上图,当添加节点 13 后,失衡的节点有 14,15,9这 3 个祖先节点,而父节点 12 和非祖先节点 6,4,8,16 都没有失衡。
因此,对于添加节点导致的失衡可以有如下 4 中情况
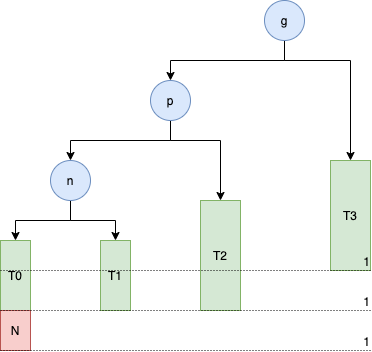
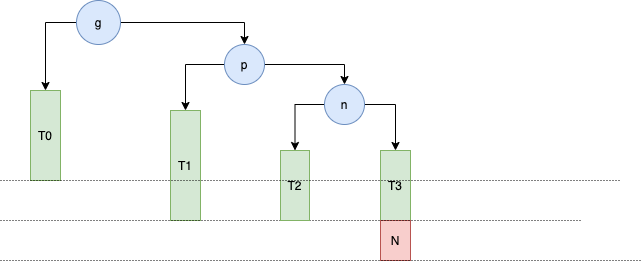
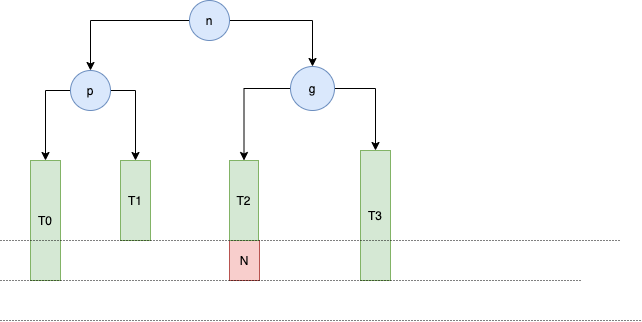
当添加节点 N 时,失衡的节点有 n 的祖父节点 g
这个时候是因为是 g 节点的左边的左边的节点使得它失去平衡,所以称这种情况为 LL,这个时候需要进行右旋转使得这个树重新获得平衡。
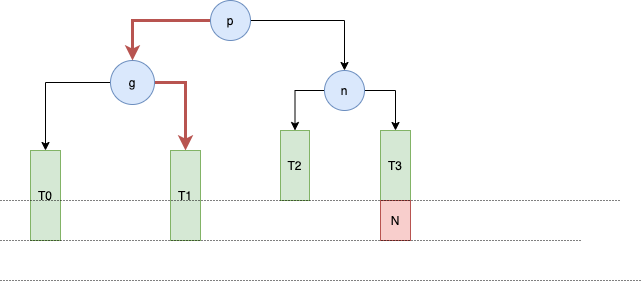
操作如下
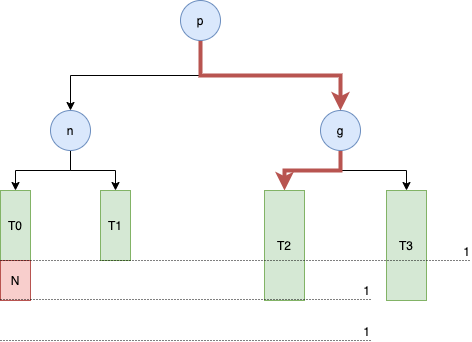
操作后如上图所示,这颗子树就恢复平衡了,同时仍然是一棵二叉搜索树:T0 < n < T1 < p < T2 < g < T3,而其他节点因为添加前后子树的高度没有变化,因此往上的祖父节点也还是平衡的。
当添加节点 N 时,失衡的节点有 n 的祖父节点 g
这个时候是因为是 g 节点的右边的右边的节点使得它失去平衡,所以称这种情况为 RR,这个时候需要进行右旋转使得这个树重新获得平衡。
变化后如下图所示
此时同样也是一颗二叉搜索树
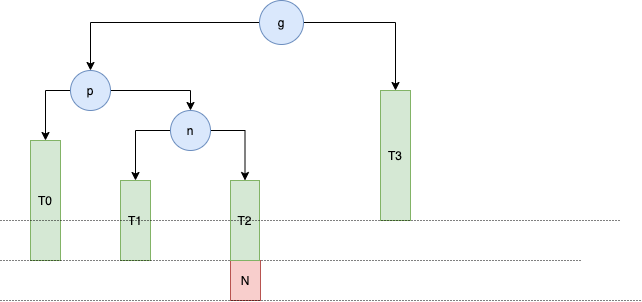
从上面的 LL,RR 的讲解,应该能猜到,是失衡节点右边的左边的节点的添加导致的。如下图所示:
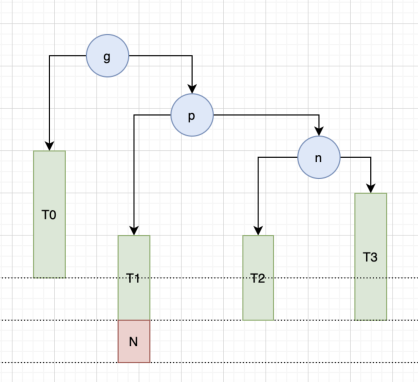
此时 g 的平衡因子是 2 失衡。此时需要做的是将这种情况转变成我们上面讲的 LL 和 RR 的情况,和玩魔方类似。讲复杂问题一步步拆分成熟悉的问题来解决。只看 n 和 p 两个节点,新添加的 N 节点是 p 节点的左边的左边,对 p 进行 LL 情况的转换。也就是对 P 进行右旋转
转换后如下图所示
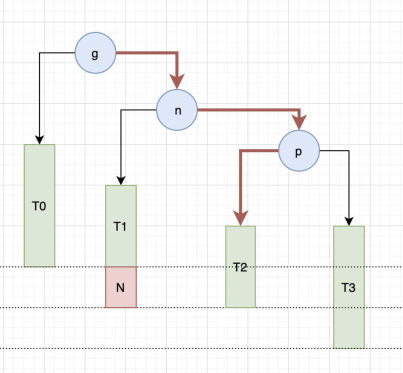
这样就变成了我们上面讲的 RR 的情况了,很简单,在对 g 进行左旋转即可。
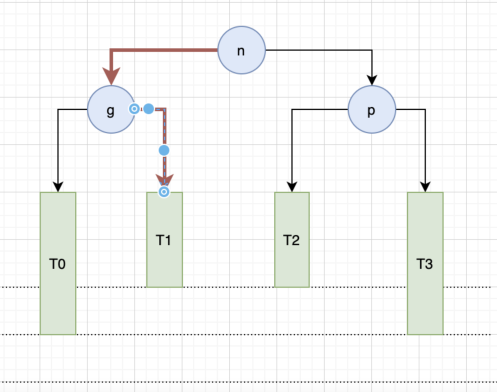
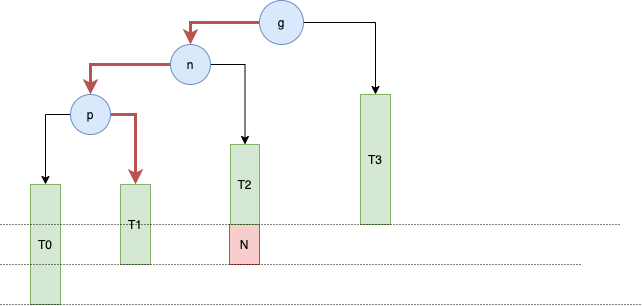
有了上面 RL 情况的分析,LR 就很简单了,直接上图
节点 g 失衡,因为其左边的右边的节点新增了节点,而单看 p,n 节点,可以简单的看成 RR 的情况,对 p 用左旋处理后
LL 的情况就形成了,下面就简单的对 g 进行右旋解决问题
至此添加导致失衡的所有情况都分析完毕,下面就是代码上如何去实现这 4 中情况了
上面分析了,失衡发现在添加之后,而我们的处理逻辑也都是在添加之后进行的,所以恢复平衡的代码也就是写在二叉搜索树添加节点之后。
在二叉搜索树的添加节点方法中添加方法afterAdd(newNode);参数为新添加的节点。
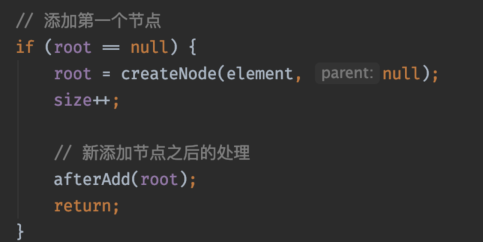

而上面的分析我们也知道了,失衡只发生在祖先节点上,而处理了最低的失衡节点后,其之上的失衡节点也会因此平衡,所以,只需要从添加节点开始向上查找第一个失衡的节点,将其平衡就可使得整个二叉搜索树平衡。
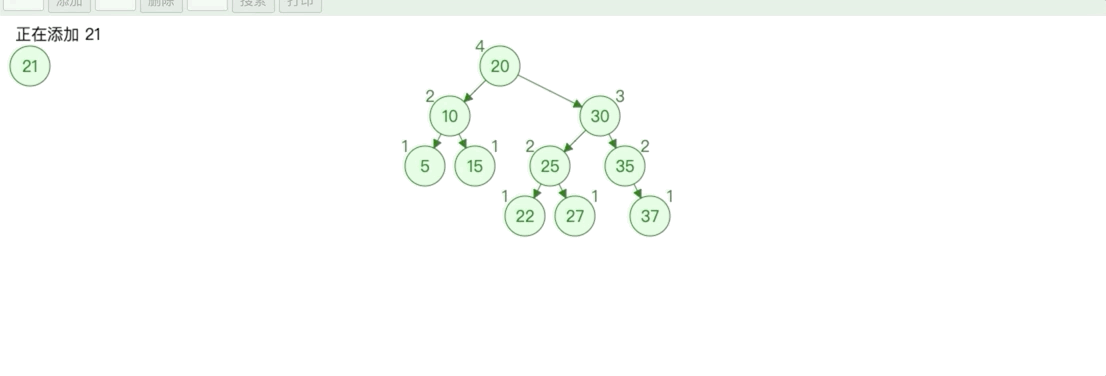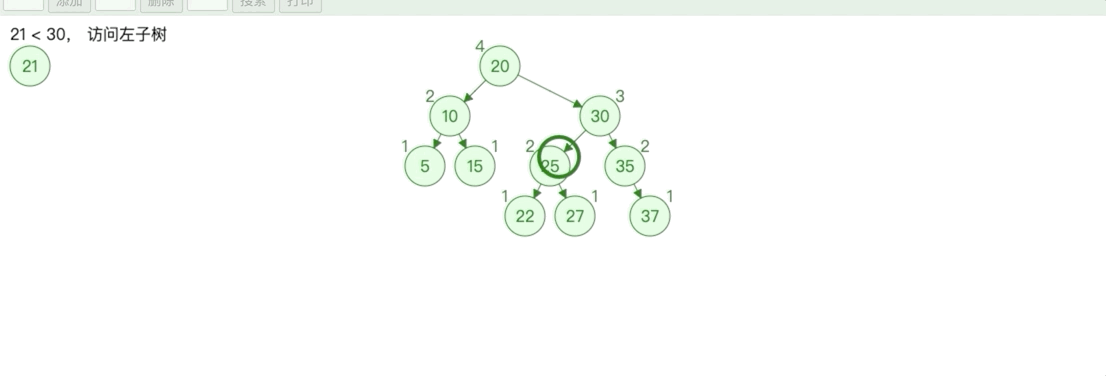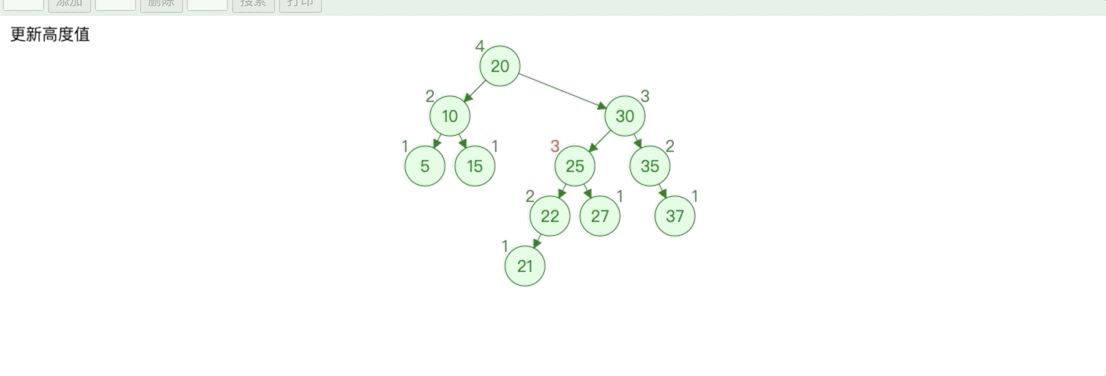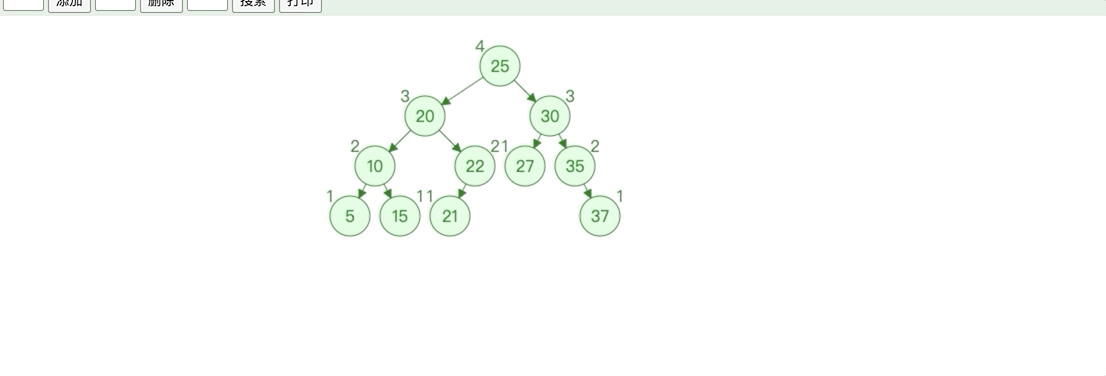
对于 AVL 树,我们需要知道其每个节点的平衡因子,AVL 树的平衡因子是左子树的高度减右子树的高度,因此我们需要知道每个节点的高度。
修改二叉搜索树中的添加节点,添加高度属性和修改高度的方式。
private static class AVLNode<E> extends Node<E> {
int height = 1;
public AVLNode(E element, Node<E> parent) {
super(element, parent);
}
public void updateHeight() {
int leftHeight = left == null ? 0 : ((AVLNode<E>) left).height;
int rightHeight = right == null ? 0 : ((AVLNode<E>) right).height;
height = 1 + Math.max(leftHeight, rightHeight);
}
}
对 AVL 树添加计算平衡因子的方法,和判断是否平衡的方法
public int balanceFactor() {
int leftHeight = left == null ? 0 : ((AVLNode<E>)left).height;
int rightHeight = right == null ? 0 : ((AVLNode<E>)right).height;
return leftHeight - rightHeight;
}
private boolean isBalanced(Node<E> node) {
return Math.abs(((AVLNode<E>)node).balanceFactor()) <= 1;
}
对于添加节点后的操作有重新设置添加节点的祖先节点的高度,找打失衡节点,恢复平衡
protected void afterAdd(Node<E> node) {
while ((node = node.parent) != null) {
if (isBalanced(node)) {
// 更新高度
updateHeight(node);
} else {
// 恢复平衡,失衡节点高度恢复后,其上节点的高度不变
rebalance(node);
// 整棵树恢复平衡
break;
}
}
}
接下来的重点就在rebalance()这个方法上。
首先分析上面的 4 中情况,当 g 是最低失衡节点时
public Node<E> tallerChild() {
int leftHeight = left == null ? 0 : ((AVLNode<E>)left).height;
int rightHeight = right == null ? 0 : ((AVLNode<E>)right).height;
if (leftHeight > rightHeight) {
return left;
}
if (leftHeight < rightHeight) {
return right;
}
return isLeftChild() ? left : right;
}
private void rebalance(Node<E> grand) {
Node<E> parent = ((AVLNode<E>)grand).tallerChild();
Node<E> node = ((AVLNode<E>)parent).tallerChild();
if (parent.isLeftChild()) { // L
if (node.isLeftChild()) { // LL
rotateRight(grand);
} else { // LR
rotateLeft(parent);
rotateRight(grand);
}
} else { // R
if (node.isLeftChild()) { // RL
rotateRight(parent);
rotateLeft(grand);
} else { // RR
rotateLeft(grand);
}
}
}
接下来就是左旋转和右旋转的代码实现了,根据上面的分析,和上节的基础,代码其实很简单
private void rotateLeft(Node<E> grand) {
Node<E> parent = grand.right;
Node<E> child = parent.left;
grand.right = child;
parent.left = grand;
afterRotate(grand, parent, child);
}
private void rotateRight(Node<E> grand) {
Node<E> parent = grand.left;
Node<E> child = parent.right;
grand.left = child;
parent.right = grand;
afterRotate(grand, parent, child);
}
private void afterRotate(Node<E> grand, Node<E> parent, Node<E> child) {
// 让parent称为子树的根节点
parent.parent = grand.parent;
if (grand.isLeftChild()) {
grand.parent.left = parent;
} else if (grand.isRightChild()) {
grand.parent.right = parent;
} else { // grand是root节点
root = parent;
}
// 更新child的parent
if (child != null) {
child.parent = grand;
}
// 更新grand的parent
grand.parent = parent;
// 更新高度
updateHeight(grand);
updateHeight(parent);
}
至此,添加节点恢复平衡二叉搜索树的代码就完成了。
首先回忆一下上一章,二叉搜索树的删除。当删除叶子节点的时候,直接删除;删除度为 1 的节点的时候,用其子节点代替被删除的节点,然后删除子节点;删除度为 2 的节点时,用其前驱节点或后继节点代替被删除的节点,然后删除其前驱节点或后继节点。所以真正删除的节点一定是叶子节点。
删除叶子节点的时候,当之前是平衡二叉搜索树,这时影响到的高度有其父节点和祖先节点,所以,也只会导致其父节点或祖先节点失衡。
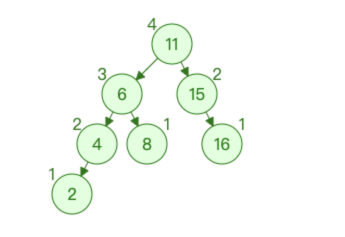
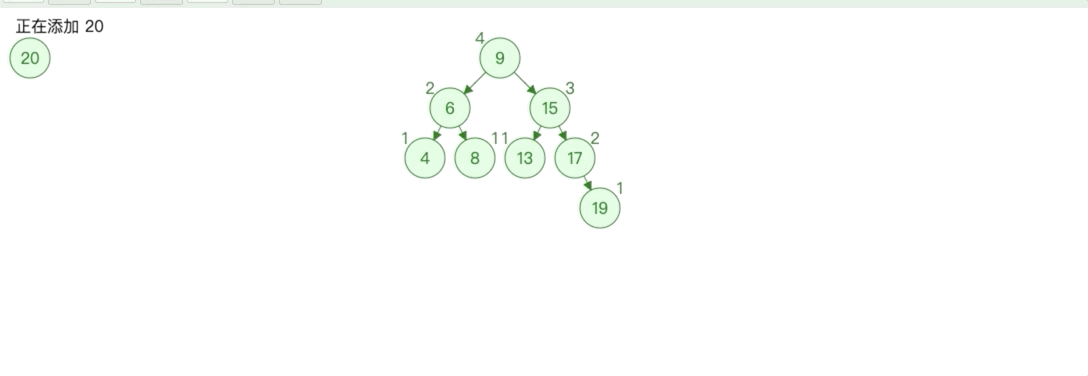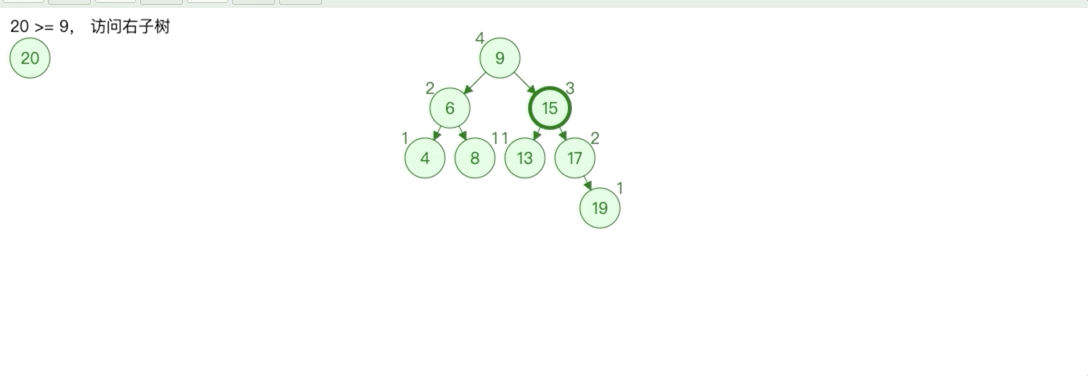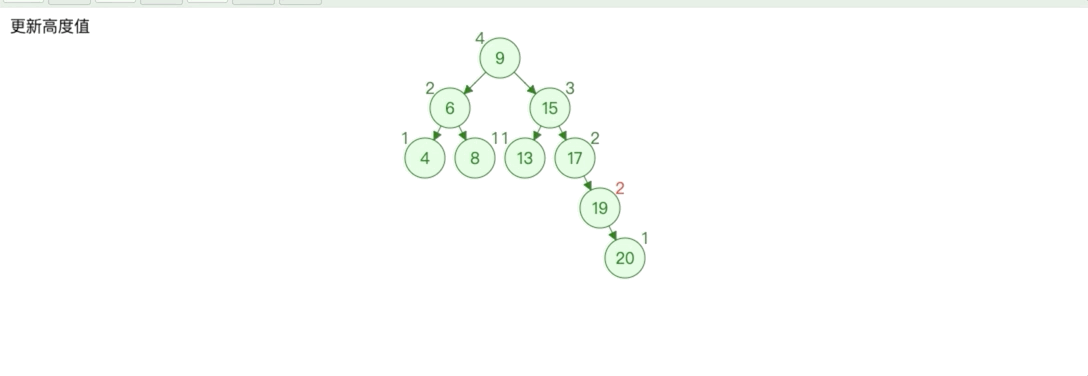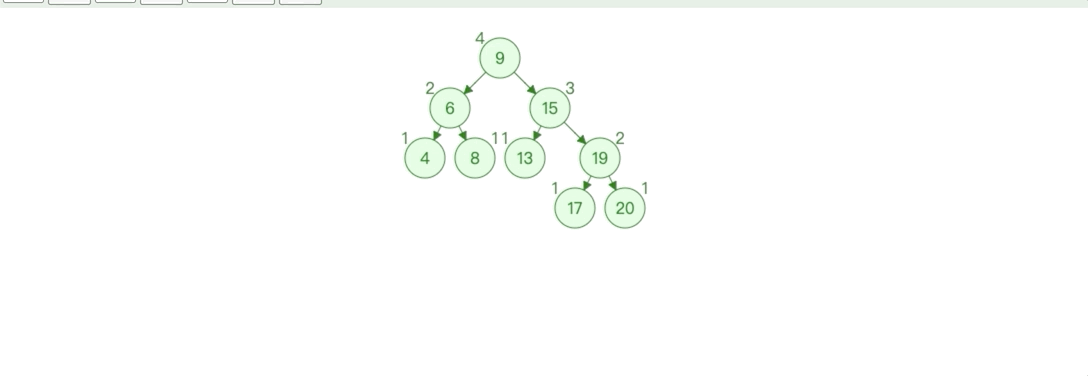
如上图所示,当删除节点 16 时,会导致节点 11 失衡。
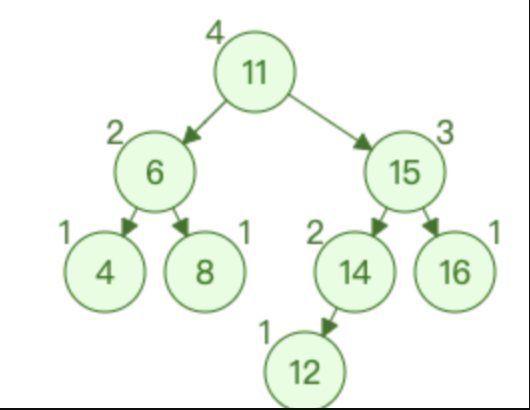
当删除节点 16 时,会造成节点 15 失衡。
对于删除同样也会出现添加那样的 4 中失衡情况。
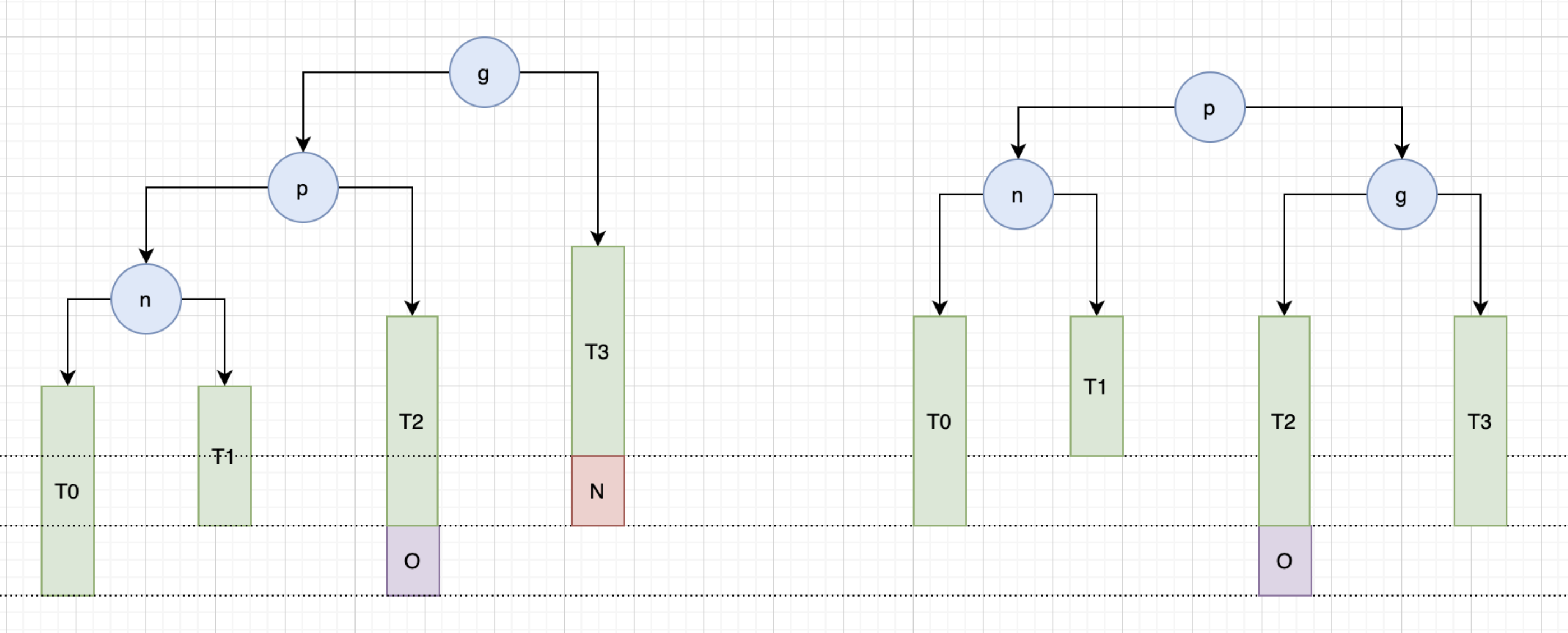
上图就是一个典型的 LL 情况,当删除 N 节点时,g 节点失衡,进行右旋转,此时整个树平衡,但是当节点 O 不存在是,整个树的高度比之前少 1,也就是说存在可能 p 的父节点失衡。
这个时候就需要继续向上查看失衡节点,同时恢复平衡
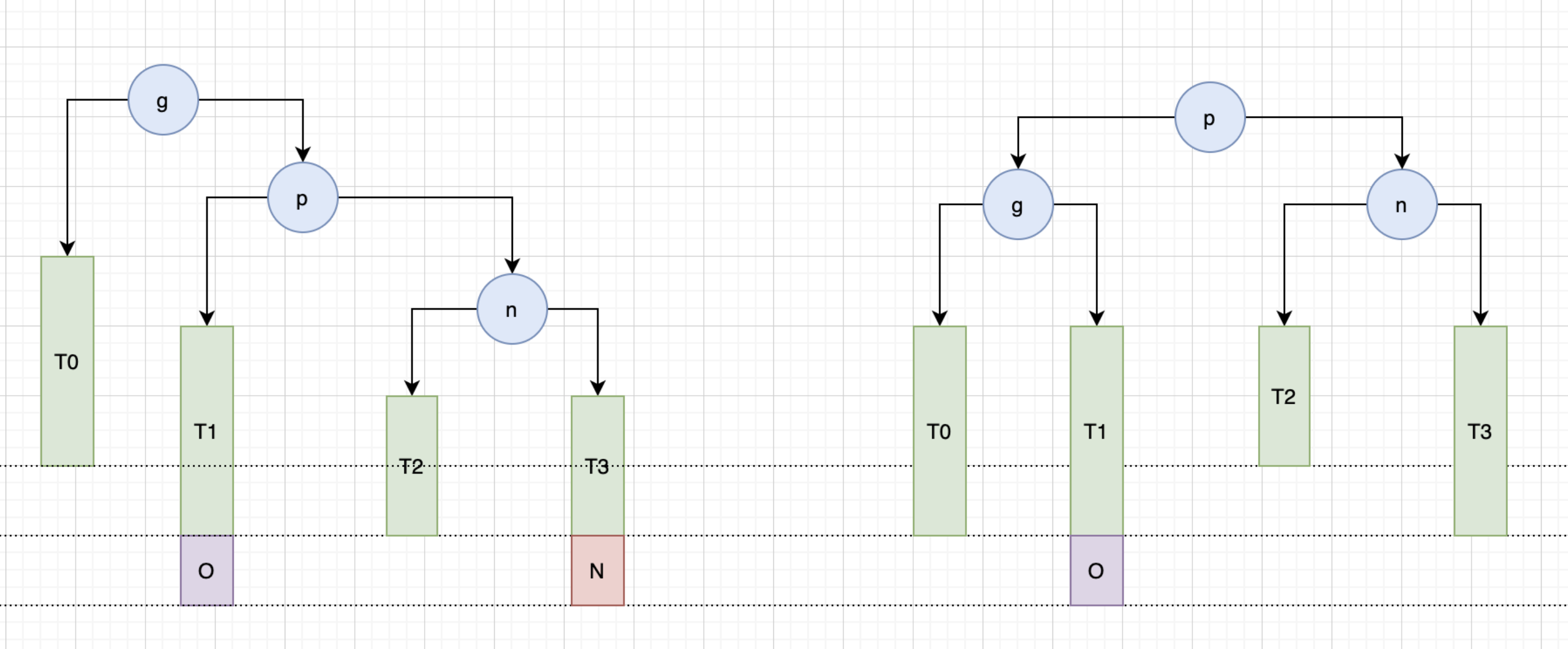
RR失衡的情况和 LL 一样,当删除节点 N 后,g 节点失衡,当 O 节点不存在时,左旋后的 p 节点的父节点可能失衡。需要继续向上查看失衡节点,并恢复平衡。
RL和 LR 的情况就不去分析了和LL 和 RR 的情形一样,经过旋转调整后,可能会出现整个子树的高度减一,从而影响到祖父节点的高度可能会出现上层节点的失衡。
在二叉搜索树的删除方法中添加恢复平衡的方法
afterRemove(node); 参数为被删除的节点

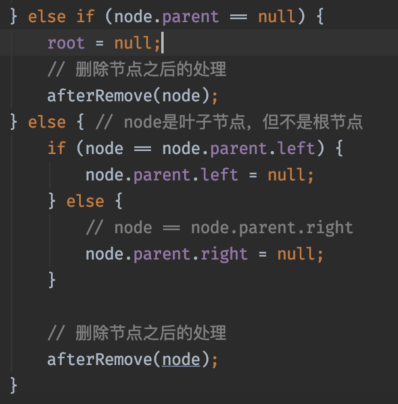
具体代码可以查看上一章节的内容。
由上面的分析可以知道。添加和删除的单次恢复都是 4 中情形,LL,RR,LR,RL。所以,恢复平衡的方法是可以通用的,唯一的不同是,添加后因为子树的高度没有发生变化,所以一次恢复就可以恢复平衡,而删除可能会引起子树高度的变化,所以需要向上层继续查看是否失衡。因此,afterRemove(node)代码的逻辑就很清楚了
protected void afterRemove(Node<E> node) {
while ((node = node.parent) != null) {
if (isBalanced(node)) {
// 更新高度
updateHeight(node);
} else {
// 恢复平衡
rebalance(node);
}
}
}
和添加方法的区别在于恢复平衡后去掉了 break;
添加
删除
最后同样留一道算法题给大家练手
推荐一个算法图形化展示的网站,也就是文中动图的来源,可以用来理解各种算法
算法网站
标签:大于 子节点 timer 变化 介绍 tree 基础 img xtend
原文地址:https://www.cnblogs.com/jinlin/p/13503570.html