构造完全图 题解

标签：一个   com   name   def   ret   mat   scan   line   find   

题目链接

分析

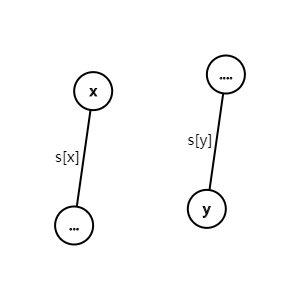
假设有如下图两个集合 \(x\) & \(y\)。因为要构造一个完全图，所以应该将\(x\)中的\(s[x]\)个节点与\(y\)中的\(s[y]\)个节点一一连接即连接\(s[x] * s[y] - 1\)（此处减一是为了在后面单独处理原图中的\(dis[i].w\)）个节点，为了保证此完全图的最小生成树所以要用\((s[x] * s[y] - 1) * (dis[i].w + 1)\)，最后加上原图中的\(dis[i].w\)。

代码

#include <cstdio>
#include <iostream>
#include <algorithm>
#define LL long long
using namespace std;
const int MAXN = 1e5 + 5;

int n, fa[MAXN], s[MAXN];
LL ans;

struct node {
	int u, v, w;
} dis[MAXN];
bool cmp (node x, node y) {
	return x.w < y.w;
}

int FindSet(int v) {
	if (fa[v] == v) {
		return v;
	} else {
		return fa[v] = FindSet(fa[v]);
	}
}

bool UnionSet(int v, int u) {
	int x = FindSet(v);
	int y = FindSet(y);
	if (x == y) return 0;
	else {
		fa[x] = fa[y];
		return 1;
	}
}

void Kruskal() {
	sort (dis + 1, dis + n, cmp);
	for (int i = 1; i <= n; i++) {
		s[i] = 1;
		fa[i] = i;
	}
	for (int i = 1; i < n; i++) {
		int x = FindSet(dis[i].u);
		int y = FindSet(dis[i].v);
		if (x == y) continue;
		ans += (long long)(dis[i].w + 1) * (s[x] * s[y] - 1) + dis[i].w;
		fa[x] = y;
		s[y] += s[x];
	} 
	printf("%lld\n", ans);
}

int main() {
	scanf ("%d", &n);
	for (int i = 1; i < n; i++) {
		scanf ("%d %d %d", &dis[i].u, &dis[i].v, &dis[i].w);
	}
	Kruskal();
	return 0;
} 

构造完全图 题解

标签：一个   com   name   def   ret   mat   scan   line   find   

原文地址：https://www.cnblogs.com/cqbz-ChenJiage/p/13513881.html