标签:space 其他 img amp 组合数 namespace ++i 直接 技术
题意:
有三个人各有x,y,z块钱,每次最多钱的人会把有1/2的概率給别人一块钱,问要给多少次,才能平均三个人的钱数。
0<x,y,z<=1e6
首先肯定是有明显的状态转移关系的。
假设x>=y>z
很容易列出dp[x][y][z]=1/2dp[x-1][y+1][z]+1/2dp[x-1][y][z+1]+1
进一步很容易想到其实有一维可以优化掉,因为最小的那个肯定不会动,我只要知道最大的和中间的比它多多少就可以了。
dp[x][y]=1/2dp[x-1][y+1]+1/2dp[x-2][y-1]+1 考虑xy分类讨论很麻烦想个简单点的
设dp[x][y]表示较小的两个差最大的多少
dp[x][y]=1/2dp[x-2][y-1]+1/2dp[x-1][y-2]+1;这个式子要求(x>=2,y>=2)
然后看一眼复杂度,xyz的和是不大的。
我们发现除了数轴的附近都是满足上面的式子的,所以说假如一个点(x,y)经过若干步走到(x1,y1)的概率是能算的,我们知道类型1走了多少次,类型2走了多少次,可以用组合数很快求出来,所以说我们处理数轴附近就好了。
dp[x][1]=1/2dp[x-2][0]+1/2dp[x][1]+1 => dp[x][1]=dp[x-2][0]+2
dp[x][0]=1/2dp[x-1][1]+1/2dp[x+1][2]+1 => dp[x][0]=1/2dp[x-1][1]+1/2(1/2dp[x][0]+1/2dp[x-1][1]+1)+1 => dp[x][0]=3/4dp[x-1][1]+1/4dp[x][0]+3/2 =>dp[x][0]=dp[x-1][1]+2
我们发现0和1的数字只设计到了内部的0和1,所以是可以dp求的。
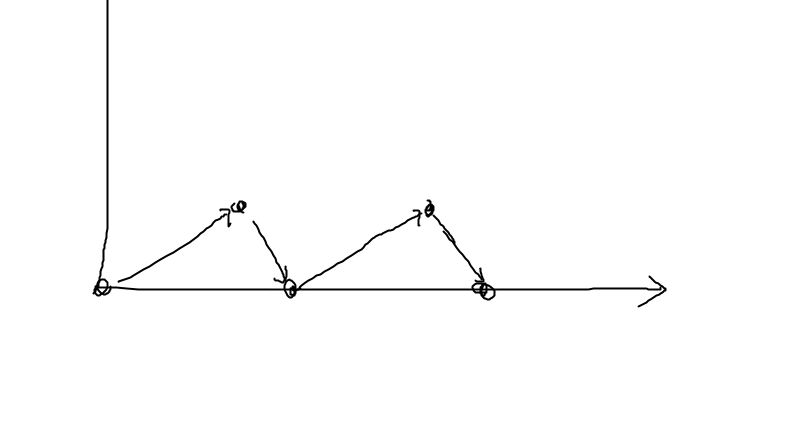
所以数轴附近的就可以做了。
写完之后的体会,感觉还是很难写的,虽然说你把一个点跑到其他点的概率都全了,但是你会发现数轴上那个高度为1的点还是能走到高度为0的点,直接算会导致重复,所以说要算到达高度0的点事,要避开高度为1的点,简单的想法就是取上一个点的概率的一半就行了,(因为到达一个点只有两个前驱,不是那个就是另外一个,而且有1/2的概率通往其他点)
#include <algorithm> #include <iostream> #include <cstring> #include <cstdio> #include <vector> #include <queue> #define R int #define I inline void #define G if(++ip==ie)if(fread(ip=buf,1,SZ,stdin)) #define lc c[x][0] #define rc c[x][1] typedef long long ll; using namespace std; const int maxn=1e6+20; const int mod=998244353; ll quick(ll a,ll b,ll m) { ll ans=1; while(b>0) { if(b&1) ans=ans*a%m; a=a*a%m; b>>=1; } return ans; } ll jiecheng[maxn]; void ini_zuhelogn() { jiecheng[0]=1; for(int i=1;i<maxn;i++) { jiecheng[i]=jiecheng[i-1]*i%mod; } } ll zuhe_logn(int m,int n) { if(jiecheng[0]!=1) ini_zuhelogn(); ll ans=((jiecheng[m]*quick(jiecheng[n], mod-2, mod))%mod)*quick(jiecheng[m-n], mod-2, mod)%mod; return ans; } int dp[maxn][2]; int main() { dp[0][0]=0; for(int i=3;i<1e6;i+=3) { dp[i-1][1]=dp[i-3][0]+2; dp[i][0]=dp[i-1][1]+2; } int T=0; ll inv_2=quick(2, mod-2, mod); scanf("%d",&T); while (T--) { int x[3]; scanf("%d%d%d",&x[0],&x[1],&x[2]); if((x[0]+x[1]+x[2])%3!=0) { printf("-1\n"); continue; } sort(x, x+3); int x1=x[2]-x[0],y1=x[2]-x[1]; ll ans=0; for(int i=3;i<=x1;i+=3) { //(i-1 1) (i ,0) //(x1,y1) int x2=x1-(i-1),y2=y1-1; int xuyao=(2*x2-y2)/3,xuyao_bu=(2*y2-x2)/3; if(xuyao<0||xuyao_bu<0) { } else { //cout<<(dp[i-1][1]+(x2+y2)/3)<<endl<<zuhe_logn((x2+y2)/3, xuyao)<<endl<<quick(inv_2, (x2+y2)/3, mod)<<endl; ans=(ans+((dp[i-1][1]+(x2+y2)/3)*zuhe_logn((x2+y2)/3, xuyao)%mod)*quick(inv_2, (x2+y2)/3, mod))%mod; } x2=x1-(i+1);y2=y1-2; xuyao=(2*x2-y2)/3;xuyao_bu=(2*y2-x2)/3; if(xuyao<0||xuyao_bu<0) { } else { //cout<<(dp[i][0]+(x2+y2)/3+1)<<endl<<zuhe_logn((x2+y2)/3, xuyao)<<endl<<quick(inv_2, (x2+y2)/3+1, mod)<<endl; ans=(ans+((dp[i][0]+(x2+y2)/3+1)*zuhe_logn((x2+y2)/3, xuyao)%mod)*quick(inv_2, (x2+y2)/3+1, mod))%mod; } } for(int i=3;i<=y1;i+=3) { //(1 i-1) (0 ,i) //(x1,y1) int x2=x1-1,y2=y1-(i-1); int xuyao=(2*x2-y2)/3,xuyao_bu=(2*y2-x2)/3; if(xuyao<0||xuyao_bu<0) { } else { //cout<<(dp[i-1][1]+(x2+y2)/3)<<endl<<zuhe_logn((x2+y2)/3, xuyao)<<endl<<quick(inv_2, (x2+y2)/3, mod)<<endl; ans=(ans+((dp[i-1][1]+(x2+y2)/3)*zuhe_logn((x2+y2)/3, xuyao)%mod)*quick(inv_2, (x2+y2)/3, mod))%mod; } x2=x1-2;y2=y1-(i+1); xuyao=(2*x2-y2)/3;xuyao_bu=(2*y2-x2)/3; if(xuyao<0||xuyao_bu<0) { } else { //cout<<(dp[i][0]+(x2+y2)/3+1)<<endl<<zuhe_logn((x2+y2)/3, xuyao)<<endl<<quick(inv_2, (x2+y2)/3+1, mod)<<endl; ans=(ans+((dp[i][0]+(x2+y2)/3+1)*zuhe_logn((x2+y2)/3, xuyao)%mod)*quick(inv_2, (x2+y2)/3+1, mod))%mod; } } if(x1==0||x1==1||y1==0||y1==1) ans=dp[x1][y1]; printf("%lld\n",ans); } } //748683271
标签:space 其他 img amp 组合数 namespace ++i 直接 技术
原文地址:https://www.cnblogs.com/King-of-Dark/p/13495054.html