查找：二叉查找树升级版平衡二叉树(AVL树) 2020年8月

时间：2020-09-07 19:09:38 阅读：57 评论：0 收藏：0 [点我收藏+]

标签：lan 平衡 load nbsp ret onclick alt 计算 http

一、实现思想

　　平衡二叉树比二叉查找树升级在哪里？

　　平衡二叉树是在二叉查找树的属性『左小右大』的基础上做一个调整，确保每一个节点的左右子树高度差不大于1，这样在运用『左小右大』进行查找时，就可以一下子排除许多数。最直观的，平衡二叉树就不会有像二叉查找树那样一边倒的例子。

　　如何确保每个节点的左右子树高度差不大于1？

　　每插入一个节点后，我都对这棵树进行检查(这个检查正是本博客的重点)，如果发现不平衡，立马做出调整。

二、实现图例

　　举一个例子

技术图片

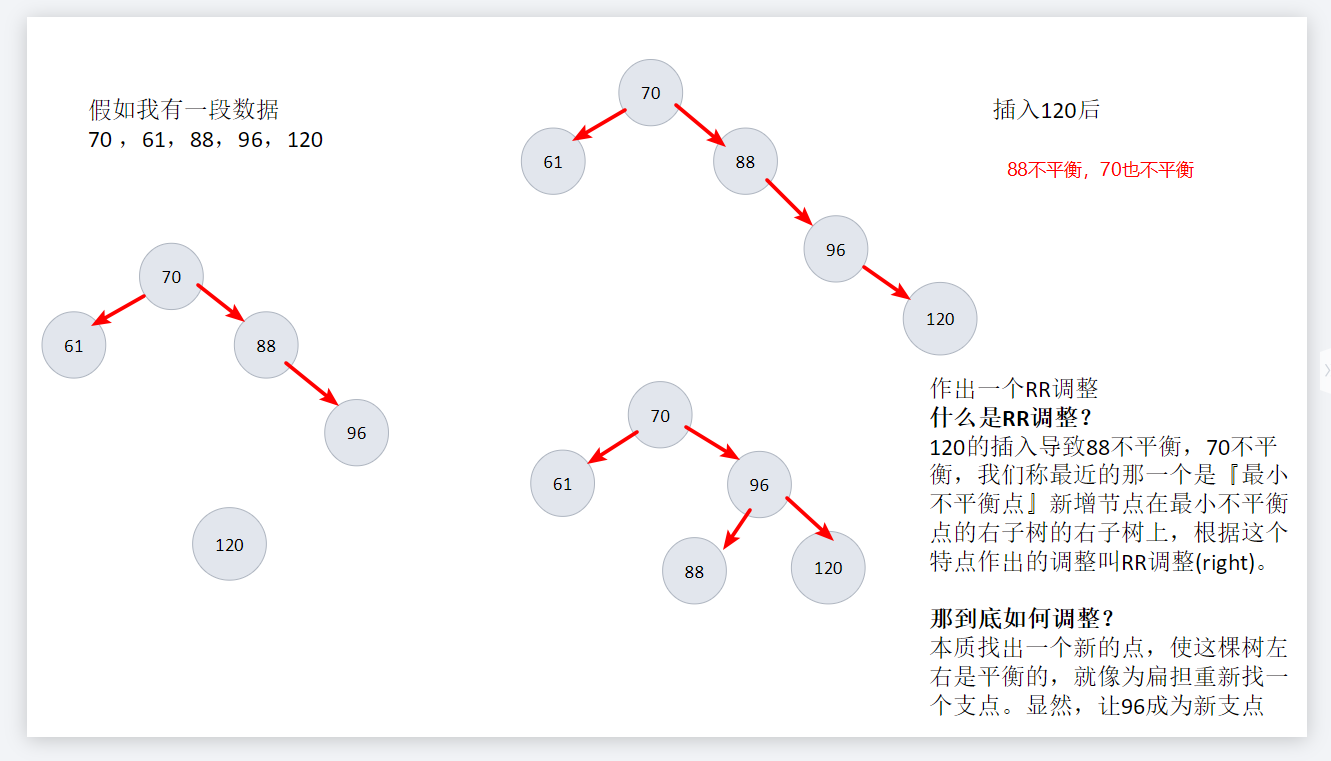
　　总结出四大情况

　　RR调整

　　LL调整

　　RL调整

　　LR调整

　　技术图片

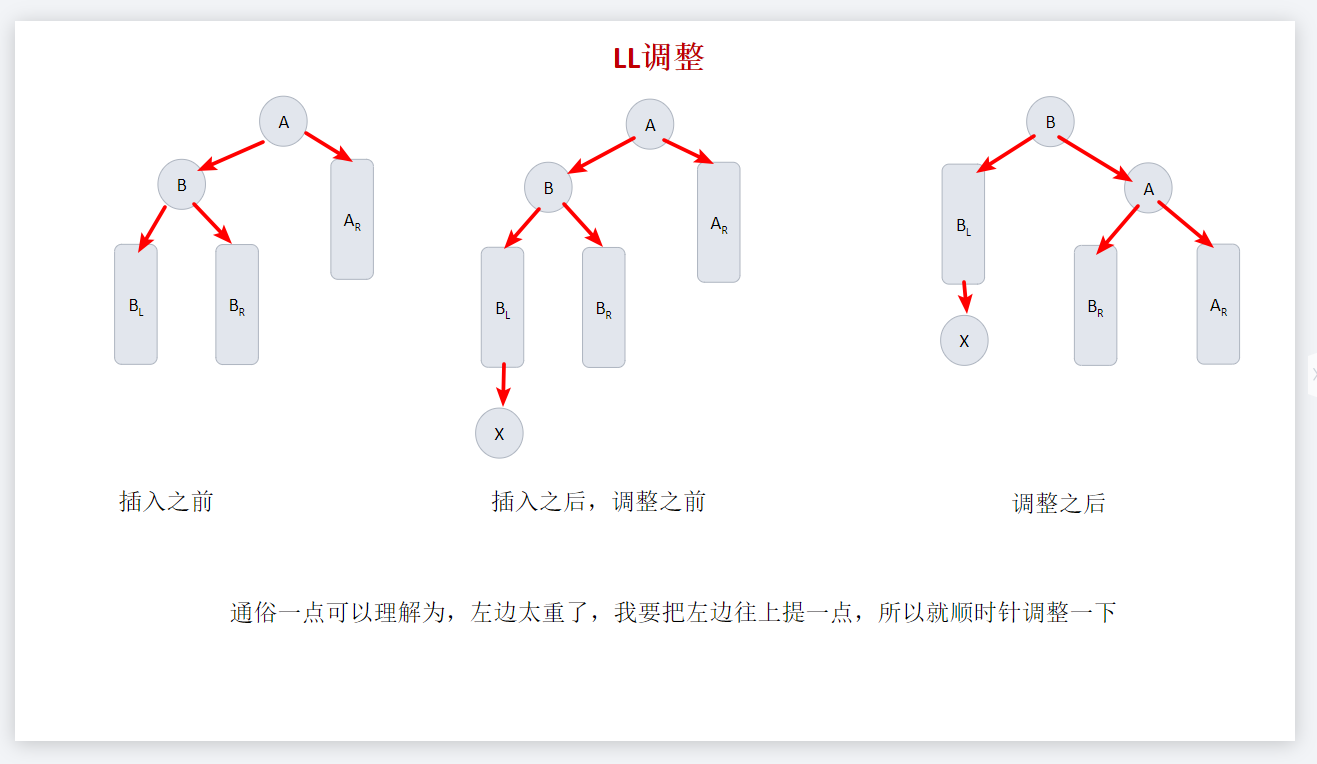
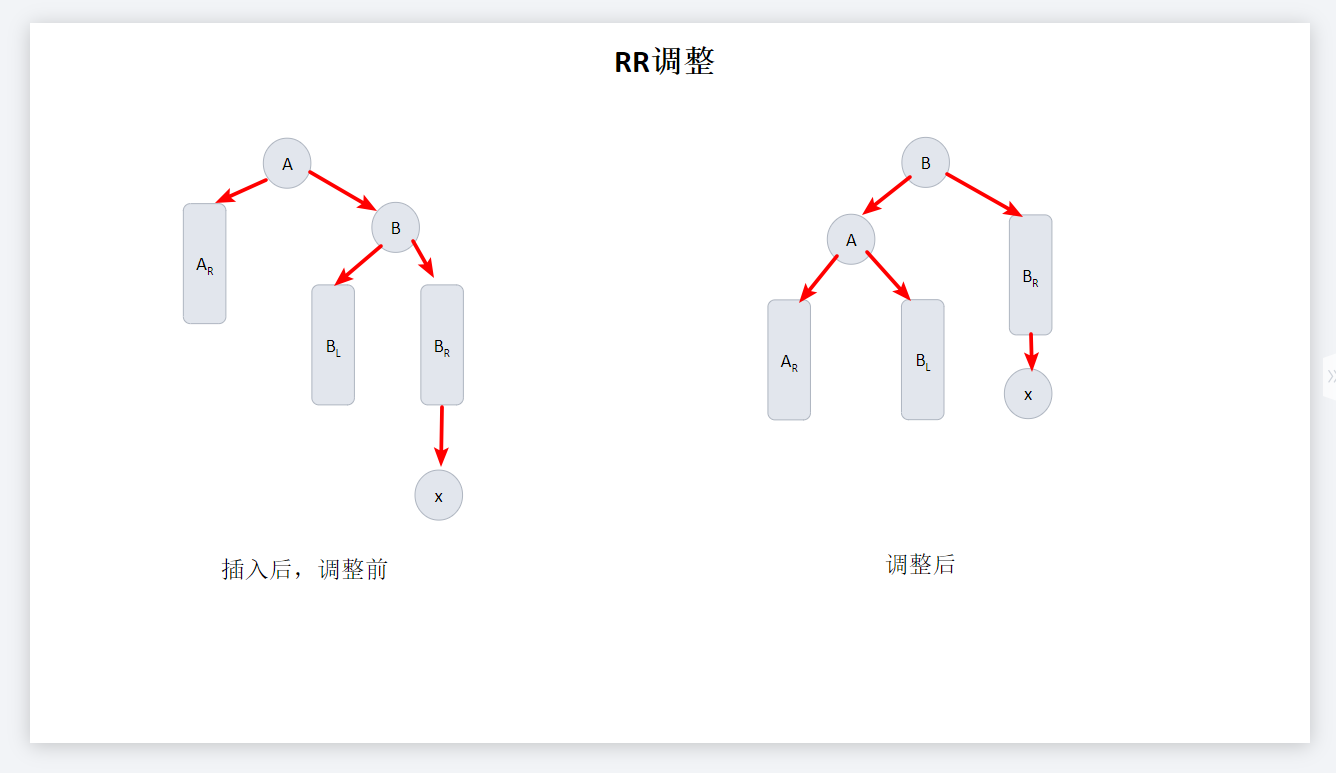
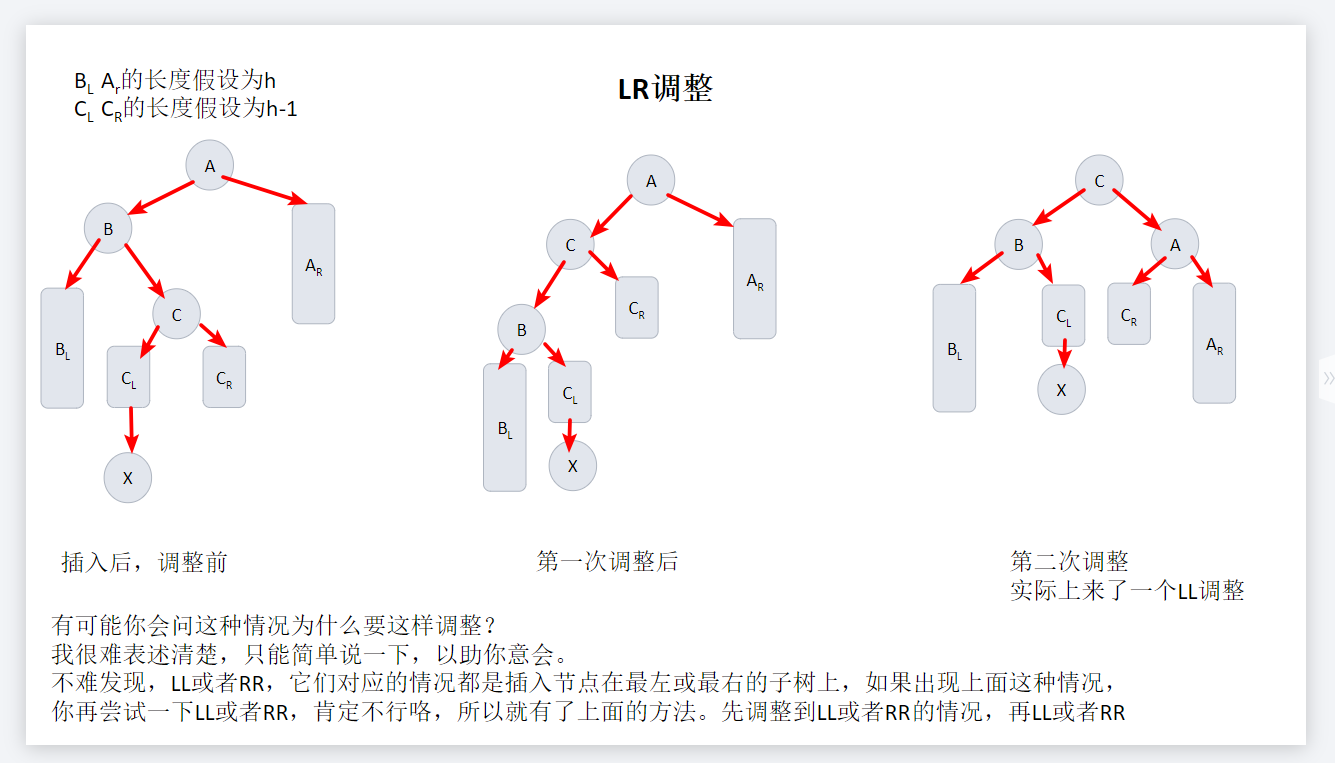
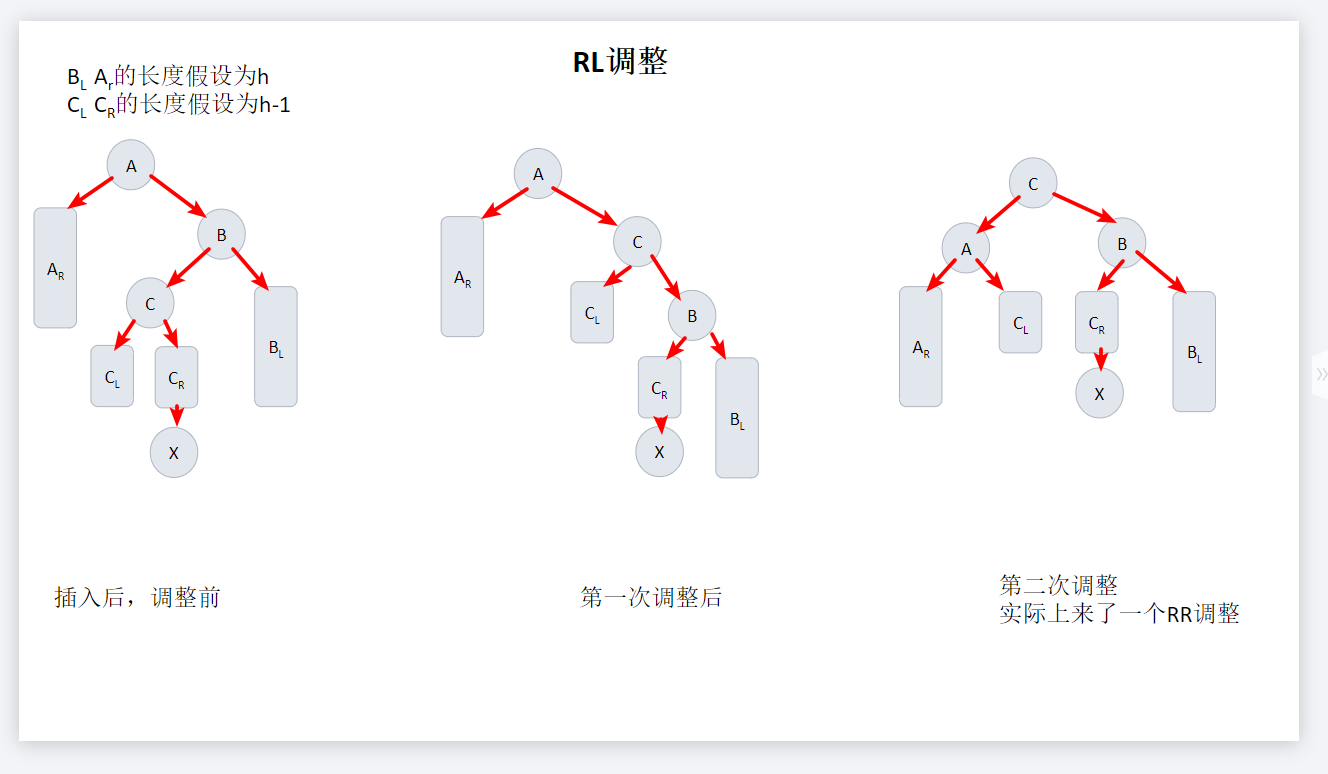
三、实现代码

　　插入的函数　　　　(其中一部分代码，这是我觉得最精华的地方，利用了递归，一次递归搞定两样事情)

　　它是递归下去寻找插入的位置
　　插入完成之后，它会层层地跳出递归，顺便检查这条路径上地节点是否平衡，不平衡则立即调整

 1 //向树中插入元素                    //不需要在全局寻找最小不平衡点，用递归就能统一格式地寻找
 2 pTree insert(pTree root, int data)
 3 {
 4 
 5     //如果为NULL，就可以new一个节点，并且把指向返回给上一个指向
 6     if (root == NULL)
 7     {
 8         pTree p = new Tree();
 9         p->data = data;
10         p->left = NULL;
11         p->right = NULL;
12         root = p;
13     }
14     else
15     {
16         if (data < root->data)
17             root->left = insert(root->left, data); //先是执行了插入操作，再去判断是否需要调整
18         if (height(root->left) - height(root->right) == 2)
19         {
20             //判断需要进行哪一种调整，只需要判断插入的data，相对于最小不平衡点的下一个节点，的位置。太妙了，我没有想到这样比较
21             if (data < root->left->data)
22                 root = LLrotation(root);
23             else
24                 root = LRrotation(root);
25         }
26         if (data >= root->data)
27             root->right = insert(root->right, data);
28         if (height(root->right) - height(root->left) == 2)
29         {
30             if (data < root->right->data)
31                 root = RLrotation(root);
32             else
33                 root = RRrotation(root);
34         }
35     }
36 
37     return root;
38 }

　　判断树高的函数　　　　(这也是我觉得比较神奇的地方，也是利用了递归)

 1 //计算一个树的高度
 2 int height(pTree root)
 3 {
 4     int hl, hr, max;
 5     if (root)
 6     {
 7         //代码太妙了，有许多递归的用法
 8         hl = height(root->left);
 9         hr = height(root->right);
10         max = hl > hr ? hl : hr;
11         return max + 1;
12     }
13     else
14         return 1;
15 }