标签：访问   style   info   二叉树的遍历   color   部分   深度优先搜索   所有结点   应用   

二叉树的遍历

树的遍历是树的一种重要的运算。所谓遍历是指对树中所有结点的信息的访问，即依次对树中每个结点访问一次且仅访问一次，我们把这种对所有节点的访问称为遍历（traversal）。那么树的两种重要的遍历模式是深度优先遍历和广度优先遍历,深度优先一般用递归，广度优先一般用队列。一般情况下能用递归实现的算法大部分也能用堆栈来实现。

深度优先遍历

对于一颗二叉树，深度优先搜索(Depth First Search)是沿着树的深度遍历树的节点，尽可能深的搜索树的分支。
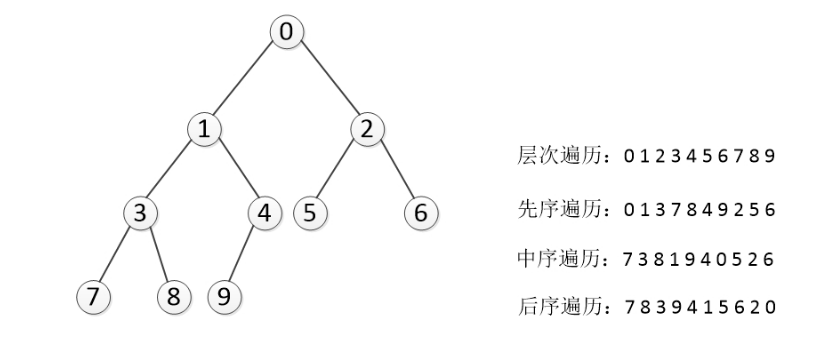
那么深度遍历有重要的三种方法。这三种方式常被用于访问树的节点，它们之间的不同在于访问每个节点的次序不同。这三种遍历分别叫做先序遍历（preorder），中序遍历（inorder）和后序遍历（postorder）。我们来给出它们的详细定义，然后举例看看它们的应用。

先序遍历 在先序遍历中，我们先访问根节点，然后递归使用先序遍历访问左子树，再递归使用先序遍历访问右子树
根节点->左子树->右子树

1 def preorder(self, root):
2       """递归实现先序遍历"""
3       if root == None:
4           return
5       print root.elem
6       self.preorder(root.lchild)
7       self.preorder(root.rchild)

中序遍历 在中序遍历中，我们递归使用中序遍历访问左子树，然后访问根节点，最后再递归使用中序遍历访问右子树
左子树->根节点->右子树

1 def inorder(self, root):
2       """递归实现中序遍历"""
3       if root == None:
4           return
5       self.inorder(root.lchild)
6       print root.elem
7       self.inorder(root.rchild)

后序遍历 在后序遍历中，我们先递归使用后序遍历访问左子树和右子树，最后访问根节点
左子树->右子树->根节点

1 def postorder(self, root):
2       """递归实现后续遍历"""
3       if root == None:
4           return
5       self.postorder(root.lchild)
6       self.postorder(root.rchild)
7       print root.elem

二叉树的前序、中序、后序遍历

标签：访问   style   info   二叉树的遍历   color   部分   深度优先搜索   所有结点   应用   

原文地址：https://www.cnblogs.com/GouQ/p/13581196.html