标签:因此 结束 上下 tin prim 排列 技术 完成 ==
深度优先搜索属于图算法的一种,是一个针对图和树的遍历算法,英文缩写为DFS即 Depth First Search。
例如,在下面的树结构中找出节点1。
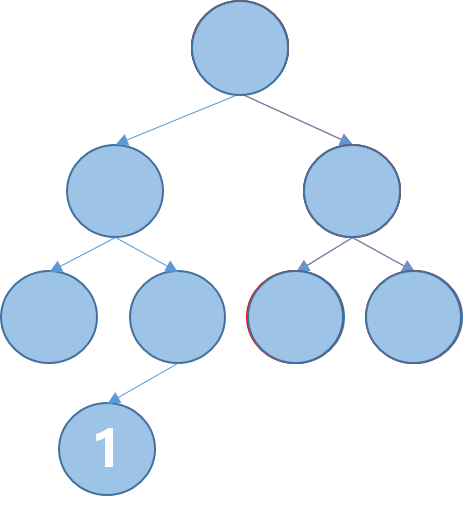
采取的策略是按照深度优先的方式进行,也就是一条路走到底。每次进入都先走左边,直到左边不能走了,退回一步,选择没有走过的路(右边)。

其中搜索实际上指得是一种穷举策略,按照该策略,将所有的可行方案全部列举出来,不断进行尝试,直到找到问题的解。
【题目描述】
给定一个由不同的小写字母组成的字符串,输出这个字符串的所有全排列。
我们假设对于小写字母有‘a’ <‘b’ < ... <‘y’<‘z’,而且给定的字符串中的字母已经按照从小到大的顺序排列。
【输入】
只有一行,是一个由不同的小写字母组成的字符串,已知字符串的长度在1到6之间。
【输出】
输出这个字符串的所有排列方式,每行一个排列。要求字母序比较小的排列在前面。
【样例输入】
abc
【样例输出】
abc
acb
bac
bca
cab
cba
题目分析:对于3个字符,我们可以假定有3个格子,每个格子中放一个字符,要求形成所有的排序顺序。明显按照字母顺序,我们从前往后选择即可,这意味着先将a放在第一个格子,然后放b在第二个格子,然后c。当3个格子都被放满了,说明形成了第一个顺序,然后考虑第二个格子放c,第三个放b,依次类推。

需要注意的是,我们的策略是,从没有选择过的字符中选择一个放入格子中,因此,我们需要给每一个字符做一个标记,用于表示这个字符的选择状态。我们在进行回退操作时,也要将选择状态重置为未选择。
#include <iostream>
#include <cstring>
using namespace std;
#define N 7
char a[N], b[N];
int n;
bool vst[N]; //用于记录选择状态
void dfs (int step) { //step当前放的格子数
if (step == n) {
for (int i = 0; i < n; i++)
cout << a[i];
cout << endl;
return ;
}
for (int i = 0; i < n; i++) { // 往step格子中存
if (!vst[i]) {
vst[i] = 1;
a[step] = b[i]; // 第step个格子中存字符b[i]
dfs(step+1);
vst[i] = 0;
}
}
}
int main () {
cin >> b;
n = strlen(b);
dfs (0);
return 0;
}
【问题描述】
在N*N的棋盘上放置N个皇后(n<=10)而彼此不受攻击(即在棋盘的任一行,任一列和任一对角线上不能放置2个皇后),编程求解所有的摆放方法。
【输入格式】
输入:n
【输出格式】
输出共有多少种摆放方案。
【输入样例】
4
【输出样例】
2
对于样例4皇后来说,我们的搜索策略一定是试着去穷举所有的可能性,那么在整个棋盘上,一定会逐行的进行尝试,尝试该放置是否能放置皇后。如下图所示
首先将皇后 放置1行1列的位置,那么相应的对角线,横竖列都不能放置。接下来从第2行找到第一个能放置的位置放。
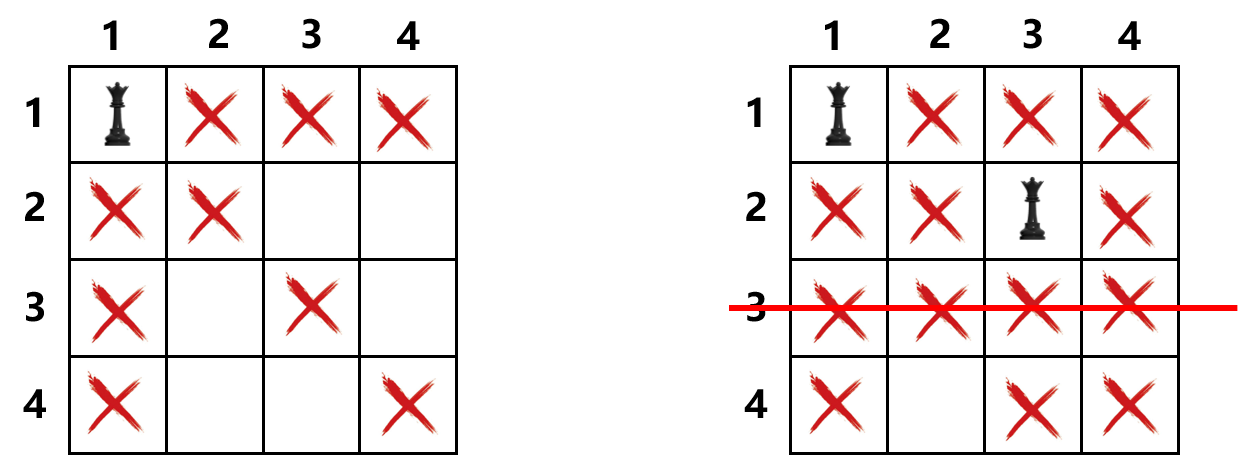
放完后发现第3行没有位置了,不满足条件。回退一步,放置2行末尾。
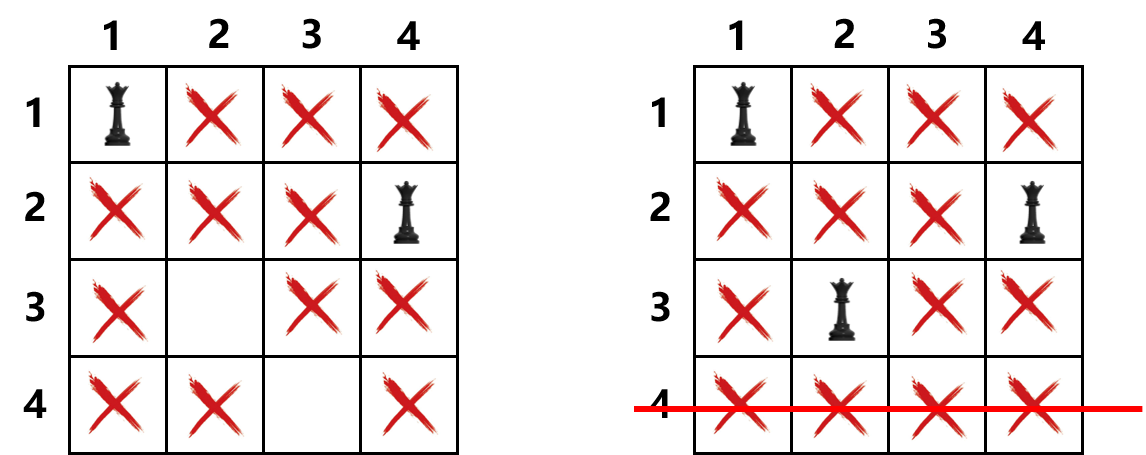
接着从3行放置,发现4行不满足条件,继续回退到第一个皇后的放置位置,尝试放置第1行第2个位置。

继续往后放置皇后

可以发现,成功的找出了一种答案。
此时需要的考虑的问题就是,如何在程序中表示?思考上述的过程发现
1、从第一个位置开始放置皇后,尝试放置,并且放好后,在同行、同列、同对角线做好不能放置皇后的标记。
2、当无法完成放置的时候,需要进行回退操作。实际上利用好递归的过程即可。
搜索时可以按层进行
参考程序
#include <iostream>
#define N 15
using namespace std;
int cnt, n;
int r[N], c[N], d1[N*2], d2[N*2];
void dfs (int floor) {
if (floor == n+1) { //顺利填完最后一层。方案数加1
cnt ++;
return ;
}
for (int i = 1; i <= n; i++) { //在floor层中寻找可以放的位置
if (!c[i] && !d1[floor+i] && !d2[n+floor-i]) { // 同行、列、对角线没有皇后
c[i] = d1[floor+i] = d2[n+floor-i] = 1;
dfs (floor+1); //找下一层
c[i] = d1[floor+i] = d2[n+floor-i] = 0;
}
}
}
int main () {
cin >> n;
dfs (1);
cout << cnt;
return 0;
}
已知 n 个整数 x1,x2,…,xn,以及1个整数k(k<n)。从n个整数中任选k个整数相加,可分别得到一系列的和。例如当n=4、k=3、4个整数分别为3、7、12、19时,可得全部的组合与它们的和为:
3+7+12=22
3+7+19=29
7+12+19=38
3+12+19=34
现在,要求你计算出和为素数共有多少种。而上述例子中只有一种和为素数:3+7+19=29。
【输入格式】
n k
x1 x2 ... xn
【输出格式】
输出满足条件的数有多少种
【输入样例】
4 3
3 7 12 19
【输出样例】
1
易错点:从n个数中选k个数,可能会有重复,例如x1,x2,x3,也可能选成x2,x1,x3。那么为了去重,只要保证选择的数在原序列的位置是递增的即可。
参考程序
#include <iostream>
using namespace std;
#define N 25
int a[N];
int n, k, cnt;
bool vst[N];
bool is_prime (int x) {
if (x < 2) return false;
for (int i = 2; i * i <= x; i++)
if (x % i == 0)
return false;
return true;
}
void dfs (int sum, int step, int before) {
if (step == k) {
if (is_prime(sum))
cnt ++;
return ;
}
for (int i = 1; i <= n; i++) {
if (!vst[i] && i > before) {
vst[i] = 1;
dfs(sum+a[i], step+1, i);
vst[i] = 0;
}
}
}
int main () {
cin >> n >> k;
for (int i = 1; i <= n; i++)
cin >> a[i];
dfs(0, 0, 0);
cout << cnt;
return 0;
}
【问题描述】
有一个大小为N×M的园子,雨后积起了水。八连通的积水被认为是连接在一起的。请求出园子里总共有多少水洼?假定‘w‘表示水洼,‘.‘表示没有水洼。所谓八连通指的是,在‘W‘的上下左右8个方向如果也有水洼,那么它们是连通的。例如下面的两个水洼是连通的。
. . W
. W .
. . .
【限制条件】
N,M <= 100
【输入格式】
第一行n和m
接下来n+1行,每行m个字符,表示园子的情况
【输出格式】
一行,表示总共多少个水洼
【样例输入】
10 12
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.
【样例输出】
3
参考程序
#include <iostream>
#include <string>
using namespace std;
const int MAXN = 100 + 5;
string a[MAXN];
int n, m;
void dfs(int x, int y)
{
a[x][y] = ‘.‘;
for (int dx = -1; dx <= 1; ++dx)
{
for (int dy = -1; dy <= 1; ++dy)
{
int nx = x + dx, ny = y + dy;
if (nx >= 0 && nx < n &&
ny >= 0 && ny < m &&
a[nx][ny] == ‘W‘)
dfs(nx, ny);
}
}
return ;
}
int main()
{
int ans = 0;
cin >> n >> m;
for (int i = 0; i < n; ++i) cin >> a[i];
for (int i = 0; i < n; ++i)
for (int j = 0; j < m; ++j)
if (a[i][j] == ‘W‘)
{
dfs(i,j);
ans++;
}
cout << ans << endl;
}
可以参考这个框架进行思考。
void dfs(....) { // DFS的参数由具体搜索策略而定
if(边界条件) {//打印、结束、比较
做相应处理
} else {
for(...) { // 枚举同层的每一种可能的情况
if() {满足条件
设置条件 //存数组、设约束(已访问等)、加总量(求总和等)
bfs(...) // 进入下一层进行搜索
恢复条件设置
}
}
}
}
标签:因此 结束 上下 tin prim 排列 技术 完成 ==
原文地址:https://www.cnblogs.com/s-k-p/p/13581735.html