标签：数据   数据集   class   类别   rac   导致   集合   输入   最小   

一、逻辑回归简介

逻辑回归又称Logistic回归分析，是一种广义的线性回归分析模型，常用于数据挖掘、疾病自动诊断、经济预测等领域。逻辑回归从本质来说属于二分类问题。
二分类问题是指预测的y值只有两个取值（0或1）。例如：一个垃圾邮件过滤系统，x是邮件的特征，预测的y值就是邮件的类别（是垃圾邮件还是正常邮件）。对于类别我们通常称为正类（positive class）和负类（negative class），在该例子中，正类就是正常邮件，负类就是垃圾邮件。

二、为什么要用逻辑回归

我们都知道线性回归，它研究的是因变量（目标）和自变量（预测器）之间的关系。通常使用曲线或直线来拟合数据点，目标是使曲线到数据点的距离差异最小。线性回归表达式：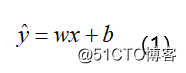

既然已经有了线性回归模型，我们为什么还要使用Logistic回归。如下图所示：在线性回归中一般使用0.5作为阈值来判断正例和负例的依据。但是在下图（b）中，如果继续使用0.5作为阈值就不合适了，会导致错误的样本分类。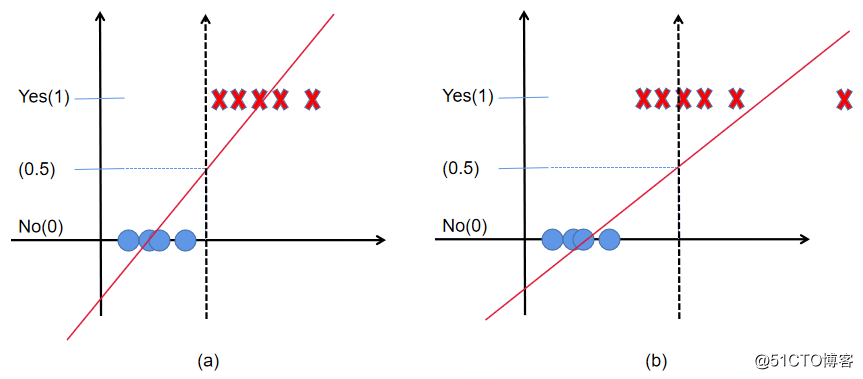

图1 线性回归在二分类中的应用
Logistic回归使用Sigmoid函数将预测值映射为(0, 1)上的概率值，帮助判断结果。如下图所示：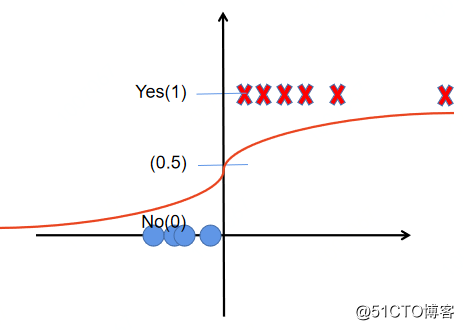

图2 Logistic回归在二分类中的应用

三、参数估计方式理解逻辑回归模型

Logistic回归函数的表达为参数化的函数, 即: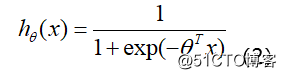

其中：hθ（x）作为事件结果y=1的概率取值，x∈Rn+1，y∈{0,1}，θ∈Rn+1表示权值向量。权值向量θ中包含偏置项，即：θ=（θ0，θ1，……，θn），x=（1，x1，x2，……，xn）。
一个事件发生的几率(odds)是指该事件发生的概率与该事件不发生的概率的比值。如果事件发生的概率是p , 那么该事件的几率为p(1-p) , 该事件的对数几率(log odds)或Logit函数是：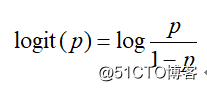

对逻辑回归而言, 根据模型表达式可以得到：

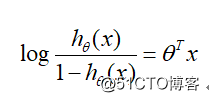
即在Logistic回归模型中，输出 y=1的对数几率是输入x的线性函数, 或者说y=1的对数几率是由输入x的线性函数表示的模型，即LR模型。
Logistic回归模型多用于解决二分类问题, 如广告是否被点击 (是／否), 商 品是否被购买 (是／否) 等互联网领域中常见的应用场景。但在实际场景中, 我们又不把它处理成绝对的分类, 而是用其预测值作为事件发生的概率。这 里从事件, 变量以及结果的角度给予解释。我们所能拿到的训练数据统称为 观测样本。问题, 样本是如何生成的？一个样本可以理解为发生的一次事件, 样本生成的过程即事件发生的过程, 对于 0/1 分类问题来讲, 产生的结果有 两种可能, 符合伯努利试验的概率假设。因此, 我们可以说样本的生成过程 即为伯努利试验过程, 产生的结果 (0/1) 服从伯努利分布, 那么对于第 i个样本, 概率公式表示如下：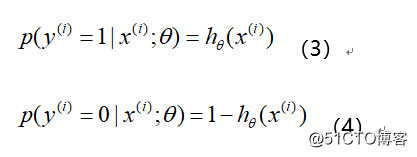

将上面两个公式合并在一起, 可以得到第 i 个样本正确预测的概率：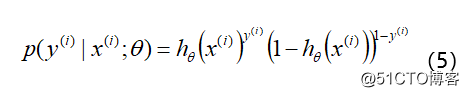

公式（5）是对一个样本进行建模的数据表达。为什么可以这么做呢？因为 y = 1 时后面一项为 1 , y = 0 时前面一项为 1 。那么对于所有的样本, 假设每条样本生成过程独立, 在整个样本空间中 ( N 个样本) 的概率分布 (即似然函数) 为：

可以通过极大似然估计方法求概率参数。如果从统计学的角度可以理解为参数 θ 似然性的函数表达式 (即似然函数表达式)。就是利用已知的样本分布, 找到最有可能 (即最大概率) 导致这种分布的参数值; 或者说什么样的参数才能使我们观测到目前这组数据的概率最大。参数在整个样本空间的似然函数可表示为：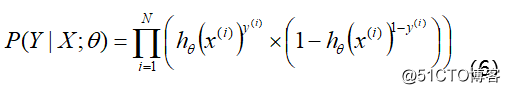

然后, 我们使用随机梯度下降的方法, 对参数进行更新：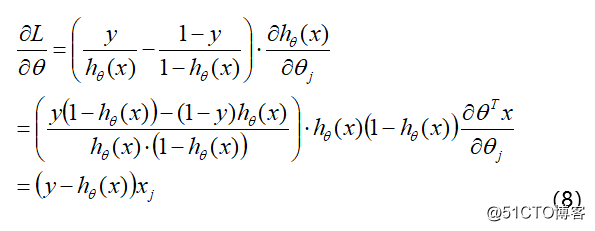

最后, 通过扫描样本, 迭代下述公式可救的参数：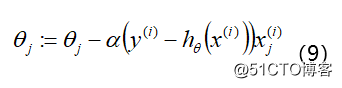

其中：α表示学习率。

四、应用逻辑回归模型

下面通过python的sklearn模块实践一下Logistic回归模型。
（4.1）Logistic回归模型的函数及参数如下所示：

import sklearn

sklearn.linear_model.LogisticRegression(penalty=‘l2‘, 
          dual=False, tol=0.0001, C=1.0, fit_intercept=True, 
          intercept_scaling=1, class_weight=None, 
          random_state=None, solver=‘liblinear‘, max_iter=100, 
          multi_class=‘ovr‘, verbose=0, warm_start=False, n_jobs=1)

（4.2）LogisticRegression类的常用方法如下所示：
fit(X, y, sample_weight=None)

拟合模型，用来训练LR分类器，其中X是训练样本，y是对应的标记向量；

返回对象，self；

fit_transform(X, y=None, **fit_params)

fit与transform的结合，先fit后transform。返回X_new:numpy矩阵；

predict(X)

用来预测样本，也就是分类，X是测试集。返回array；

predict_proba(X)

输出分类概率。返回每种类别的概率，按照分类类别顺序给出。如果是多分类问题，multi_class="multinomial"，则会给出样本对于

每种类别的概率；

返回array-like；

score(X, y, sample_weight=None)

返回给定测试集合的平均准确率（mean accuracy），浮点型数值；

对于多个分类返回，则返回每个类别的准确率组成的哈希矩阵。

（4.3）实战

（4.3.1）加载模块

import numpy as np
from sklearn import linear_model, datasets
from sklearn.model_selection import train_test_split

（4.3.2）加载数据集

# 2. 加载数据

iris = datasets.load_iris()
x_data = iris.data
y_label = [1 if i>=1 else 0 for i in iris.target]
print("x_data: \n", x_data[:10])
print("\n")
print("label_data: \n",y_label[:10])

x_data数据有4个特征，y的值有两类（0和1）；

（4.3.3）拆分数据集为：训练集和测试集

# 3. 拆分数据集

X_train, X_test, Y_train, Y_test = train_test_split(x_data, y_label, test_size=0.3, random_state=0)

（4.3.4）训练模型

# 4. 训练逻辑回归模型

log_reg = linear_model.LogisticRegression()
log_reg.fit(X_train, Y_train)

（4.3.5）在测试数据集上预测效果

# 5. 预测

test_data_proba = log_reg.predict_proba(X_test)
accuracy = log_reg.score(X_test, Y_test)

print("test data proba value: \n", test_data_proba[:10])
print("\n"*2)
print("test data true value: \n", Y_test[:10])
print("\n"*2)
print("test data accuracy is :", accuracy)

结果如下所示：
（a）预测的概率值，第一列为预测为0的概率，第二列预测为1的概率；

（b）可以看到Logistic模型的效果还不错哦，在测试集上的准确率为100%。

一个数据人的自留地是一个助力数据人成长的大家庭，帮助对数据感兴趣的伙伴们明确学习方向、精准提升技能。
扫码关注我，带你探索数据的神奇奥秘

逻辑回归介绍与应用

标签：数据   数据集   class   类别   rac   导致   集合   输入   最小   

原文地址：https://blog.51cto.com/14915210/2525583