标签:核心 单源最短路 cin 初始 最简 技术 适合 优先 names
宽度优先搜索算法(又称广度优先搜索算法)是最简单的图的搜索算法之一,这一算法也是很多重要的图的算法的原型。Dijksta单源最短路径算法和Prim最小生成树算法都采用了与宽度优先搜索类似的思想。
宽度优先搜索的核心思想是:从初始结点开始,应用算符生成第一层结点,检查目标结点是否在这些后继结点中,若没有,再用产生式规则将所有第一层的结点逐一扩展,得到第二层结点,并逐一检查第二层结点中是否包含目标结点。若没有,再用算符逐一扩展第二层所有结点……,如此依次扩展,直到发现目标结点为止 。
【问题描述】
大楼的每一层楼都可以停电梯,而且第i层楼(1≤i≤N)上有一个数字Ki(0≤Ki≤N)。电梯只有两个按钮:上,下。上下的层数等于当前楼层上的那个数字。求从A楼到B楼至少要按几次按钮呢?
例如有5层楼,从1到5层每层楼的数字为3 3 1 2 5。那么要从1楼到5楼,可以先从1到4楼,然后4楼减2到2楼,从2楼加3到5楼,总共要3次。
【输入格式】
共两行
第一行为3个用空格隔开的正整数,表示N,A,B(1≤N≤200, 1≤A,B≤N)。
第二行为N个用空格隔开的非负整数,表示Ki。
【输出格式】
一行,即最少按键次数,若无法到达,则输出-1。
【输入样例】
5 1 5
3 3 1 2 5
【输出样例】
3
问题分析:可以应用宽度优先搜索,从初始状态1层楼开始,在这一层的基础上进行扩展,所有一步能到的楼,都是第二层的节点,同时记录移动步数,在把所有第二层的节点全部取出,按照扩展规则扩展到第3层楼,同理记录下移动步数。重复这个过程,直到找到最终目标。注意在这个过程中需要判断重复。可以靠队列先进先出的特点,来实现。
参考程序
#include <iostream>
#include <queue>
#define INF 0x7fffffff
#define N 205
#define P pair<int, int >
using namespace std;
int n, A, B, k[N], dis[N];
int bfs() {
queue <P> q;
dis[A] = 0;
q.push(P(A, dis[A]));
while (!q.empty()) {
int t = q.front().first;
int d = q.front().second;
q.pop();
if (t + k[t] <= n) {
if (dis[t+k[t]] > d+1) {
dis[t+k[t]] = d+1;
q.push(P(t+k[t], d+1));
}
}
if (t - k[t] >= 1) {
if (dis[t-k[t]] > d+1) { //更新距离
dis[t-k[t]] = d+1;
q.push(P(t-t[k], d+1));
}
}
}
if (dis[B] == INF)
dis[B] = -1;
return dis[B];
}
int main () {
cin >> n >> A >> B;
for (int i = 1; i <= n; i++) {
cin >> k[i];
dis[i] = INF;
}
cout << bfs() << endl;
return 0;
}
宽度优先搜索适合于找最短路径,因为沿着深度逐层扩展的,只要能找到那么一定是最短的路径。在这个过程中需要注意节点的状态表示(数据结构)、扩展规则、路径记录、重复判断。
【问题描述】
给定一个N?M的迷宫,每一步可以向上下左右四个方向走动,求出从起点到终点所需的最小步数
(’#’,’.’,‘S’,‘G’分别表示墙壁,通道,起点和终点)
【输入格式】
第一行n m
接下来n行每行m个字符
【输出格式】
输出一行,最小的步数
【样例输入】
10 10
#S######.#
......#..#
.#.##.##.#
.#........
##.##.####
....#....#
.#######.#
....#.....
.####.###.
....#...G#
【样例输出】
22
思路:
有起点和终点,只需要按层搜索扩展下去,扩展的过程中,需要判定是否撞墙或者超出界限。同时做好判重,和记录。
参考程序
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int INF = 100000;
const int MAX = 101;
typedef pair<int, int> P;
char map[MAX][MAX];
int d[MAX][MAX];//表示起点到各个位置的最短距离
int sx, sy, gx, gy;//表示起点和终点坐标
int n, m;
int dx[4] = {1, 0, -1, 0};
int dy[4] = {0, 1, 0, -1};
bool Check(int x, int y) {
if(x>=0 && x<n && y>=0 && y<m && d[x][y]==INF && map[x][y]!=‘#‘)
return true;
else return false;
}
int bfs() {
queue<P> que;
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j++)
d[i][j] = INF;
que.push(P(sx, sy));
d[sx][sy] = 0;
while(!que.empty()) {
P p = que.front();
que.pop();
if(p.first == gx && p.second == gy)
break;
for(int i = 0; i < 4; i++) {
int nx = p.first + dx[i];
int ny = p.second + dy[i];
if(Check(nx, ny)) {
que.push(P(nx, ny));
d[nx][ny] = d[p.first][p.second] + 1;
}
}
}
return d[gx][gy];
}
int main() {
cin >> n >> m;
for(int i = 0; i < n; i++) {
for(int j = 0; j < m; j++) {
cin >> map[i][j];
if(map[i][j] == ‘S‘) {
sx = i;
sy = j;
}
if(map[i][j] == ‘G‘) {
gx = i;
gy = j;
}
}
}
int res = bfs();
cout<< res <<endl;
return 0;
}
在3×3的棋盘上,摆有八个棋子,每个棋子上标有1至8的某一数字。棋盘中留有一个空格,空格用0来表示。空格周围的棋子可以移到空格中。要求解的问题是:给出一种初始布局(初始状态)和目标布局(为了使题目简单,设目标状态为123804765),找到一种最少步骤的移动方法,实现从初始布局到目标布局的转变。
【输入格式】
输入初始状态,一行九个数字,空格用0表示
【输出格式】
只有一行,该行只有一个数字,表示从初始状态到目标状态最少需要的移动次数
【输入样例】
283104765
【输出样例】
4
只思考简单的宽度优先搜索,那么8数码问题,也是从一个初始状态出发,找到一个最终状态,求最短的路径。
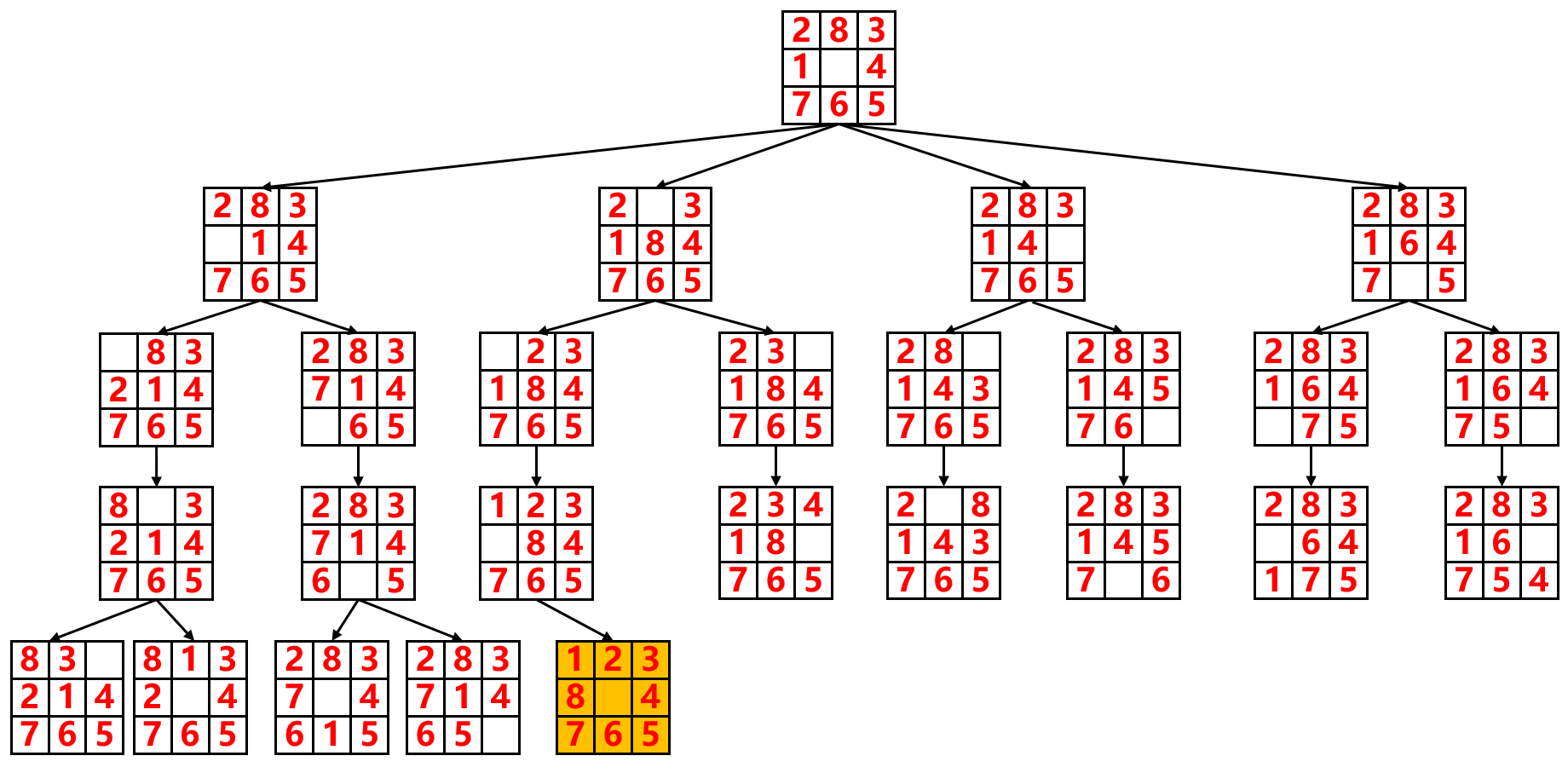
难点就变成了怎么样去表示每一个层数的状态,如何在按层数搜索扩展的时候,进行判重。
由于是一个3×3的矩阵,可以每一行的数字连接成一个9位数,进行状态的存储。常规的判重操作是通过布尔或者整型数组,用下标来记录状态,但是9位数的数组太大不合适。因此可以使用map来判重,状态用关键值(key)表示,走到该状态花费的步数用键值(value)表示,判重可以通过map的内置方法count()来查找键值。
还有注意的是数组和状态值之间的转换。
参考程序
#include <iostream>
#include <algorithm>
#include <queue>
#include <map>
using namespace std;
#define N 15
int mat[N][N];
int st, ed = 123804765;
queue <int> q;
map<int, int> m;
int dx[4] = {0, 1, 0, -1};
int dy[4] = {1, 0, -1, 0};
int zx, zy;
void to_mat (int x) {
int nu = 100000000;
for (int i = 1; i <= 3; i ++)
for (int j = 1; j <= 3; j++) {
mat[i][j] = x / nu % 10;
nu /= 10;
if (mat[i][j] == 0) {
zx = i, zy = j;
}
}
}
int to_num () {
int res = 0;
for (int i = 1; i <= 3; i++)
for (int j = 1; j <= 3; j++)
res = res * 10 + mat[i][j];
return res;
}
int bfs () {
int res;
m[st] = 0;
q.push (st);
while (!q.empty()) {
int now = q.front();
q.pop();
if(now == ed) {
res = m[ed];
break ;
}
to_mat(now);
for (int i = 0; i < 4; i++) {
int tx = dx[i] + zx;
int ty = dy[i] + zy;
if (tx > 0 && tx < 4 && ty > 0 && ty < 4) {
swap(mat[zx][zy], mat[tx][ty]);
int to = to_num();
if (!m.count(to)) {
m[to] = m[now] + 1;
q.push(to);
}
swap(mat[zx][zy], mat[tx][ty]);
}
}
}
return res;
}
int main () {
cin >> st;
cout << bfs ();
return 0;
}
void bfs(起始点) {
将起始点放入队列中;
标记起点访问;
while(如果队列不为空){
访问队列队首元素x;
删除队首元素;
if(出现最终状态) {
做相应处理
}
for(遍历所有x下一层节点){
if(该点未被访问过且合法){
将该点加入队列末尾;
做相应操作:记录距离,更新前置结点等
}
}
}
队列为空,广搜结束;
}
标签:核心 单源最短路 cin 初始 最简 技术 适合 优先 names
原文地址:https://www.cnblogs.com/s-k-p/p/13598668.html