标签:回溯 node 参数 集合 一个 数据 lis 解释 递归
给定一棵二叉树(结构如下),其中每个节点值为整数。给定一个值K,求所有满足如下条件的路径并将路径上节点的值打印出来:
1、路径方向必须向下,即只能从父节点指向子节点
2、路径并不是必须从根节点开始或在叶节点结束。即树上任意节点开始向下走到任意节点的路径都允许。
3、路径上的节点得分之和等于给定值K。节点得分=节点值+节点所在层(根节点为0,之后每层+1)。
l 示例:给定二叉树[5,3,7,9,null,11,2,4,-1, null,null,2,-2],K=22
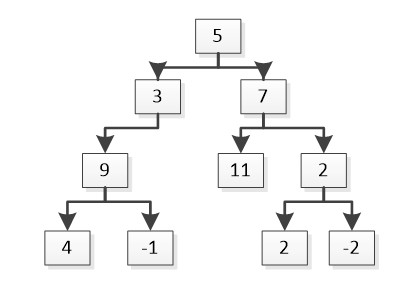
输出:
5 3 9 -1
5 7 2 2
3 9 4
解释:如第一个路径5 3 9 -1,路径上节点得分分别为5+0,3+1,9+2,-1+3,和为22
l 输入格式: 第一行为一个整数K,第二行为一个二叉树的层次遍历序列,其中空子树用 null 表示,每两个数字或者null之间用空格分隔,例如:
22
5 3 7 9 null 11 2 4 -1 null null 2 -2
需要注意的是,null节点的子节点不会显式的写出来,如上例中第二行值为3的节点的右子树为空,则该右空子树的左右子树不会再以null表示。
l 输出格式: 分为多行,每行为一个满足条件的路径上节点的值的序列,例如:
5 3 9 -1
5 7 2 2
3 9 4
现有如下输入:
35
5 4 8 11 null 13 4 7 2 null null 5 1 8 null 7 10 6 null null null
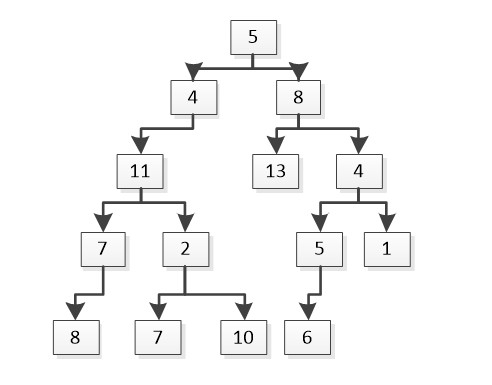
请用程序将正确结果输出
1.题目表面上想要查找出所有符合条件的路径,其实更深层次考察的是,如何构造二叉树
2.如题目所述,二叉树的层次遍历序列是直接从中控台输入的,仅仅依靠此序列来层次构造二叉树。这与我们以往的说法不同,通常需要两条序列(比如前序和中序)来构造二叉树,或者构造完全二叉树的时候,可以直接使用前序遍历序列。
3.题目还有一个要求,null节点的子节点不会显式的写出来,如上例中第二行值为3的节点的右子树为空,则该右空子树的左右子树不会再以null表示。
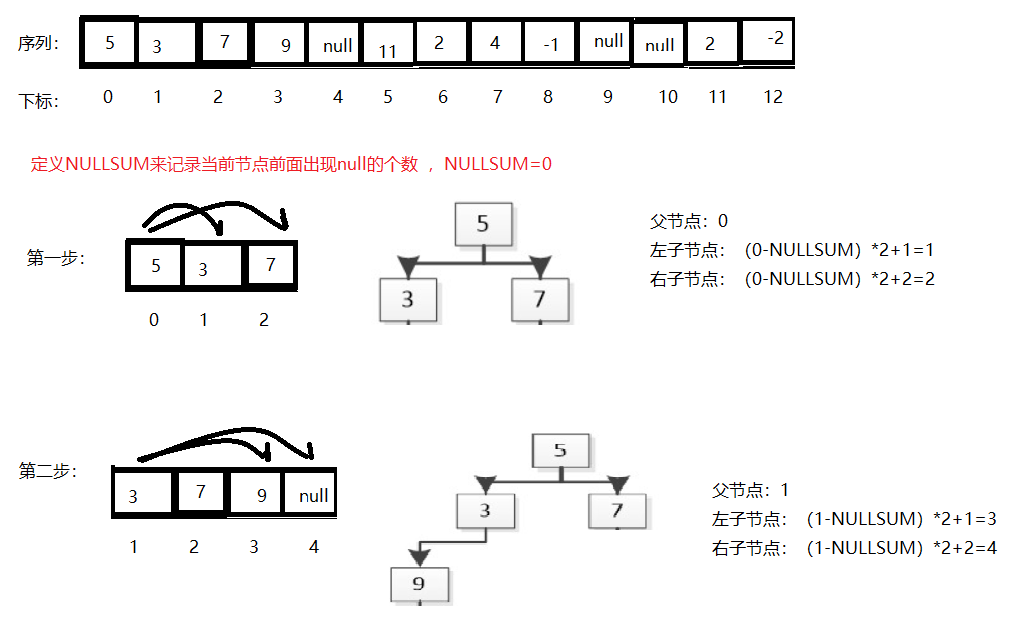
4.层次构造二叉树过程:
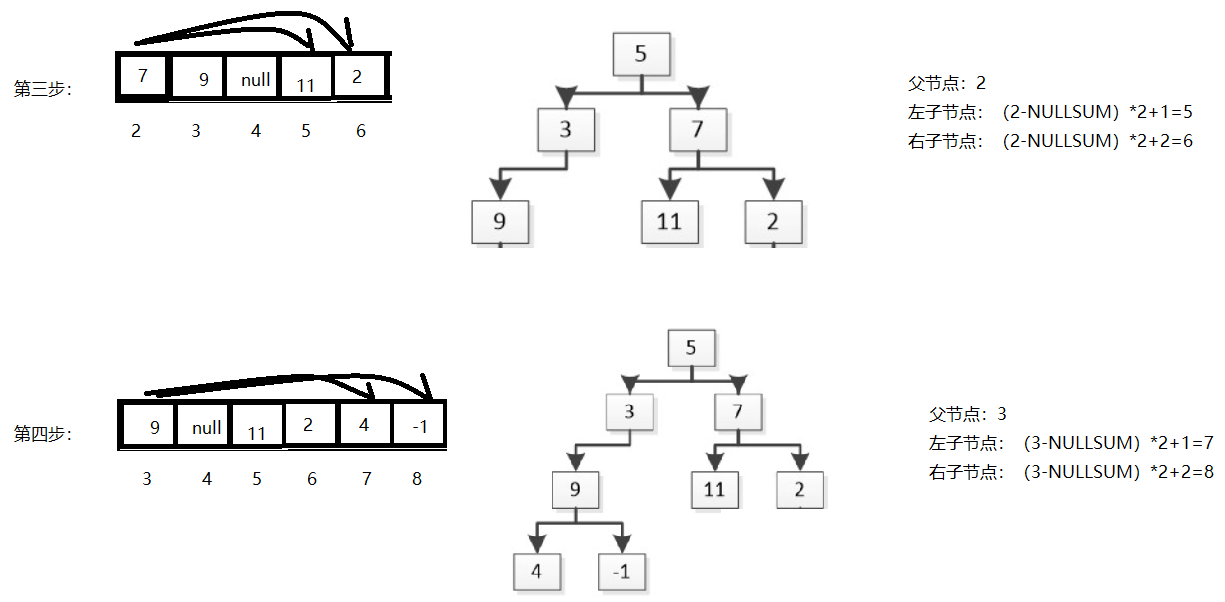
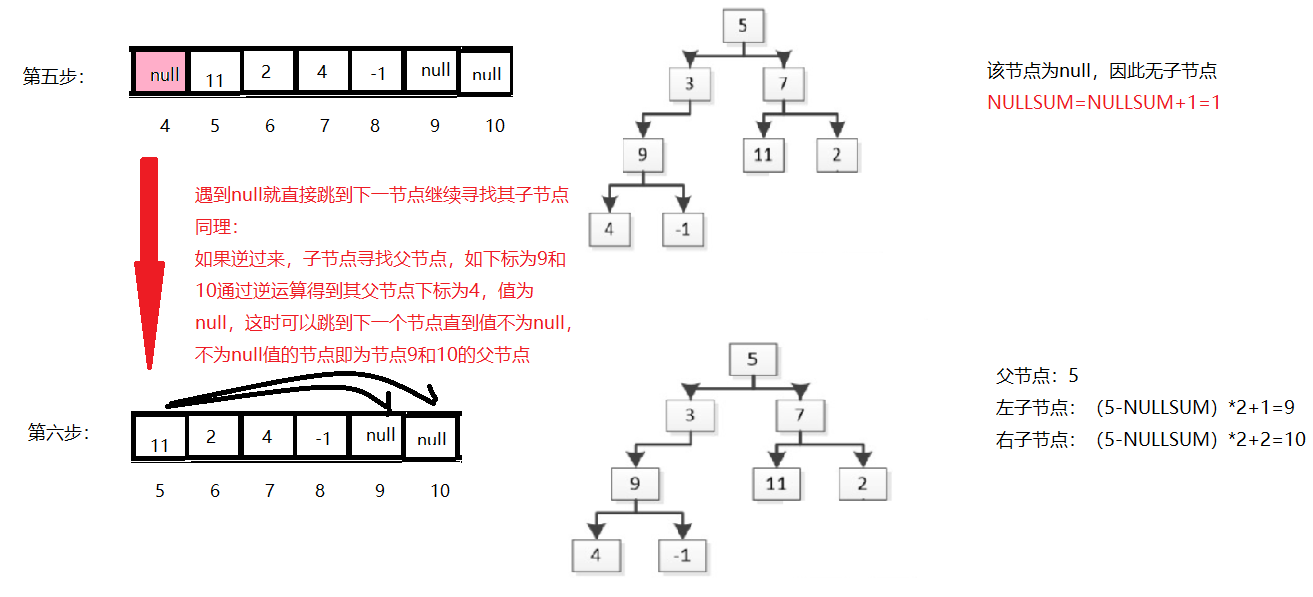
第五步和第六步中间红色字段很重要,这是子节点找父节点的思路
5.上面的分析是从上到下,按层次分析,通过父节点找其子节点,很好理解。但是代码实现无法做到这一点,我们只能由子节点找其父节点,怎么说呢?
原因是,父节点找其子节点,我们通常会想到用递归,非常简单,直接套用公式(n-NULLSUM)*2-x,这里n表示父节点下标,x表示左右(左为一,右为二),一直找下去。但是仔细会发现,这里的NULLSUM值可能不正确,
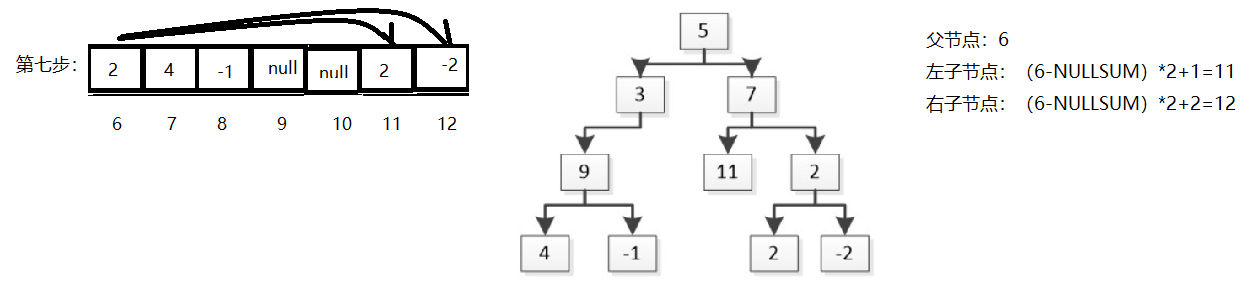
在递归构造二叉树的过程中,无法发做到层次构造,它更像前序遍历构造形式。比如上图,从根节点的右节点7开始,读到11,此时11节点的下标是5,此时(5-NULLSUM)*2+1=11得到左子节点2的下标,这里NULLSUM为什么是0呢?11节点的前面有null节点啊,NULLSUM不应该是1吗?我们在看一下NULLSUM的定义:统计当前节点前面出现null值的节点。嗯我们理解的定义没有问题,问题出现在递归调用上,它不层次算法,而是一头扎到底再回头的那种,这就导致读到11这个节点的时候,跳过了下标为4的null节点,故NULLSUM值还是为0。
6.基于以上问题,如何做到层次构造二叉树呢?
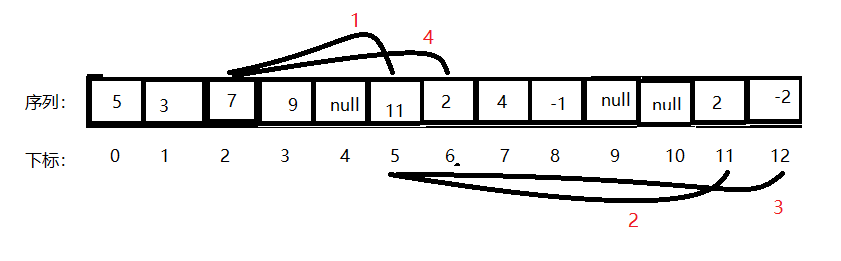
这里我想到了一个办法,那就是让子节点找父节点,这样做的好处是,一对一思想,找到父节点,就可以跳到下一个节点继续寻找其父节点。那么还有个问题,怎么知道当前节点是父节点的左节点还是右节点?其实很简单,可以在第四点的层次构造二叉树过程图中可以发现,每个节点的左节点的下标一定是奇数,右节点的下标一定是偶数,那么可以根据当前节点的下标奇偶性判断其是左节点还是右节点。
子节点找父节点,可以通过(n-NULLSUM)*2-x这个公式的逆运算算出父节点的下标n,在利用树的遍历查询,即可找到父节点
7.不知道大家发现第六点又产生了个问题,那就是利用树的遍历查询,因为从中控台输入一连串序列,这个序列中的数可以不唯一,可重复,导致构造的树每个节点的值不唯一,那么树的遍历就不好使了。如何解决这个问题呢?其实很简单,既然节点的值不唯一,那我们可以在树的数据结构里,给节点增加一个下标变量用来标识该节点,比如:
1 public class TreeNode { 2 public int val; 3 /* 4 * 由于题目给的二叉树中节点值不唯一, 5 * 增加treeIndex做唯一标识 6 */ 7 public int treeIndex;//对应数组下标 8 public TreeNode left; 9 public TreeNode right; 10 //由于数组为String类型,需要转型为整型,方便后面运算 11 public TreeNode(String x) { 12 val = Integer.parseInt(x); 13 } 14 15 public TreeNode() { 16 17 } 18 19 @Override 20 public String toString() { 21 return "TreeNode [val=" + val + "]"; 22 } 23 24 25 }
1.1、寻找父节点
1 public TreeNode searchNode(TreeNode root,int index) {//广度优先搜索,查找父节点 2 if(root==null||index<0)return null; 3 LinkedList<TreeNode> list = new LinkedList<>();//链表,这里我将其作为队列 4 list.add(root);//把数据加入到队列尾部 5 while(!list.isEmpty()) { 6 TreeNode node = list.poll(); 7 if(node.treeIndex==index) 8 return node; 9 if(node.left!=null) 10 list.add(node.left); 11 if(node.right!=null) 12 list.add(node.right); 13 } 14 15 return null; 16 }
1.2、处理传入的序列
1 public TreeNode create(String[] levelOrder) {//考虑到给的数组有null值,故用String类型 2 if(levelOrder.length==0) 3 return null; 4 TreeNode root = new TreeNode(levelOrder[0]);//根节点 5 LinkedList<Integer> list = new LinkedList<>();//链表,这里我将其作为队列 6 for(int i=1;i<levelOrder.length;i++) { 7 if(levelOrder[i]==null||"null".equals(levelOrder[i])) { 8 list.add(i); 9 continue; 10 } 11 TreeNode node = new TreeNode(levelOrder[i]); 12 node.treeIndex = i; 13 14 LinkedList<Integer> newList = new LinkedList(); 15 for (Iterator iterator = list.iterator(); iterator.hasNext();) { 16 newList.add((Integer) iterator.next()); 17 18 } 19 buildTree(root,node,i,newList,levelOrder); 20 21 } 22 return root; 23 }
1.3、建立二叉树
1 //建立树 2 public TreeNode buildTree(TreeNode root,TreeNode node,int i,LinkedList<Integer> list,String[] levelOrder) { 3 int NULLSUM = compareIndex(list,levelOrder,i); 4 /* 5 * 如题目给的示例:给定二叉树[5,3,7,9,null,11,2,4,-1, null,null,2 ,-2] 6 * index: 0,1,2,3, 4 ,5 ,6,7, 8, 9 , 10 ,11,12 7 * 8 * 5 9 * / 10 * 3 7 11 * / / 12 * 9 11 2 13 * / \ / 14 * 4 -1 2 -2 15 * 思路:1.定义NULLSUM变量记录null节点个数 16 * 2.通过compareIndex函数计算该节点的父节点层及以上出现null节点个数 17 * 3.(i-2)/2+NULLSUM可以计算出该节点的父节点 18 */ 19 if(i%2==0) { 20 TreeNode parent = searchNode(root,(i-2)/2+NULLSUM); 21 while(parent==null) { 22 NULLSUM++; 23 parent = searchNode(root,(i-2)/2+NULLSUM); 24 } 25 parent.right = node; 26 }else { 27 TreeNode parent = searchNode(root,(i-1)/2+NULLSUM); 28 while(parent==null) { 29 NULLSUM++; 30 parent = searchNode(root,(i-1)/2+NULLSUM); 31 } 32 parent.left = node; 33 } 34 35 return root; 36 }
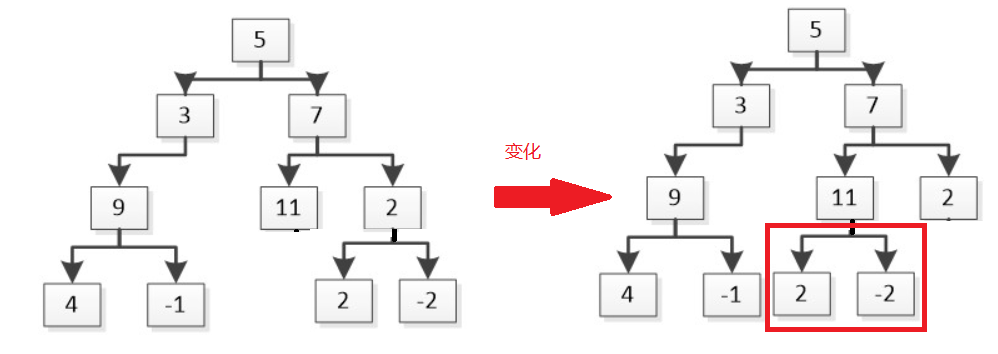
为什么在第21和28行设立while循环判断找到的父节点是否为null?还记得下面这张图吗,父节点为null时,就会跳到下一个不为null的节点来代替指向原本父节点的子节点。逆过来,子节点找父节点,如果父节点时null,那可以跳到下一个直至不为null的父节点

2、二叉树路径查找
2.1、路径查找入口
1 /* 2 * 传入的参数分别为根节点root、定值K和当前节点所在层数dept(这个非常好用,因为传入的根节点有可能只是树中某节点) 3 */ 4 public List<List<Integer>> pathSumEntry(TreeNode root,int K,int dept){ 5 List<List<Integer>> result = new LinkedList<List<Integer>>();//用于保存所有匹配路径 6 List<Integer> currentResult = new LinkedList<Integer>();//用于保存找到的当前匹配的路径 7 pathSum(root,K,currentResult,result,dept); 8 return result; 9 }
2.2、路径查找主函数
1 /* 2 * 这里主要使用递归加回溯的思想 3 */ 4 public void pathSum(TreeNode root,int K,List<Integer>currentResult,List<List<Integer>>result,int dept) { 5 if(root==null)return; 6 currentResult.add(new Integer(root.val)); 7 if(root.left==null&&root.right==null&&K==root.val+dept) { 8 result.add(new LinkedList(currentResult)); 9 }else { 10 pathSum(root.left,K-root.val-dept,currentResult,result,dept+1); 11 pathSum(root.right,K-root.val-dept,currentResult,result,dept+1); 12 } 13 currentResult.remove(currentResult.size()-1); 14 }
1.树的数据结构

1 public class TreeNode { 2 public int val; 3 /* 4 * 由于题目给的二叉树中节点值不唯一, 5 * 增加treeIndex做唯一标识 6 */ 7 public int treeIndex;//对应数组下标 8 public TreeNode left; 9 public TreeNode right; 10 //由于数组为String类型,需要转型为整型,方便后面运算 11 public TreeNode(String x) { 12 val = Integer.parseInt(x); 13 } 14 15 public TreeNode() { 16 17 } 18 19 @Override 20 public String toString() { 21 return "TreeNode [val=" + val + "]"; 22 } 23 24 25 }
2.构造二叉树类

1 public class BuildTree { 2 3 public TreeNode searchNode(TreeNode root,int index) {//广度优先搜索,查找父节点 4 if(root==null||index<0)return null; 5 LinkedList<TreeNode> list = new LinkedList<>();//链表,这里我将其作为队列 6 list.add(root);//把数据加入到队列尾部 7 while(!list.isEmpty()) { 8 TreeNode node = list.poll(); 9 if(node.treeIndex==index) 10 return node; 11 if(node.left!=null) 12 list.add(node.left); 13 if(node.right!=null) 14 list.add(node.right); 15 } 16 17 return null; 18 } 19 20 21 public TreeNode create(String[] levelOrder) {//考虑到给的数组有null值,故用String类型 22 if(levelOrder.length==0) 23 return null; 24 TreeNode root = new TreeNode(levelOrder[0]);//根节点 25 LinkedList<Integer> list = new LinkedList<>();//链表,这里我将其作为队列 26 for(int i=1;i<levelOrder.length;i++) { 27 if(levelOrder[i]==null||"null".equals(levelOrder[i])) { 28 list.add(i); 29 continue; 30 } 31 TreeNode node = new TreeNode(levelOrder[i]); 32 node.treeIndex = i; 33 34 LinkedList<Integer> newList = new LinkedList(); 35 for (Iterator iterator = list.iterator(); iterator.hasNext();) { 36 newList.add((Integer) iterator.next()); 37 38 } 39 buildTree(root,node,i,newList,levelOrder); 40 41 } 42 return root; 43 } 44 45 46 //建立树 47 public TreeNode buildTree(TreeNode root,TreeNode node,int i,LinkedList<Integer> list,String[] levelOrder) { 48 int NULLSUM = compareIndex(list,levelOrder,i); 49 /* 50 * 如题目给的示例:给定二叉树[5,3,7,9,null,11,2,4,-1, null,null,2 ,-2] 51 * index: 0,1,2,3, 4 ,5 ,6,7, 8, 9 , 10 ,11,12 52 * 53 * 5 54 * / 55 * 3 7 56 * / / 57 * 9 11 2 58 * / \ / 59 * 4 -1 2 -2 60 * 思路:1.定义NULLSUM变量记录null节点个数 61 * 2.通过compareIndex函数计算该节点的父节点层及以上出现null节点个数 62 * 3.(i-2)/2+NULLSUM可以计算出该节点的父节点 63 */ 64 if(i%2==0) { 65 TreeNode parent = searchNode(root,(i-2)/2+NULLSUM); 66 while(parent==null) { 67 NULLSUM++; 68 parent = searchNode(root,(i-2)/2+NULLSUM); 69 } 70 parent.right = node; 71 }else { 72 TreeNode parent = searchNode(root,(i-1)/2+NULLSUM); 73 while(parent==null) { 74 NULLSUM++; 75 parent = searchNode(root,(i-1)/2+NULLSUM); 76 } 77 parent.left = node; 78 } 79 80 return root; 81 } 82 83 /* 84 * 比较下标所指向的值,判断当前节点的父节点下标所在数组位置的值是否等于null 85 * list为存储空值的下标队列,从头到尾取值,并计算比较当前节点下标比栈值的子节点大 86 * 若大于,这NULLSUM++,否则停止,返回NULLSUM值 87 */ 88 public int compareIndex(LinkedList<Integer> list,String[] order,int i) { 89 int sum,NULLSUM = 0;//记录数组中null的数量 90 if(list==null&&list.size()==0) { 91 return 0; 92 } 93 while(!list.isEmpty()&&i>list.poll()*2) { 94 NULLSUM++; 95 } 96 return NULLSUM; 97 } 98 99 100 }
3.路径查找类

1 public class PathSum { 2 3 /* 4 * 传入的参数分别为根节点root、定值K和当前节点所在层数dept(这个非常好用,因为传入的根节点有可能只是树中某节点) 5 */ 6 public List<List<Integer>> pathSumEntry(TreeNode root,int K,int dept){ 7 List<List<Integer>> result = new LinkedList<List<Integer>>();//用于保存所有匹配路径 8 List<Integer> currentResult = new LinkedList<Integer>();//用于保存找到的当前匹配的路径 9 pathSum(root,K,currentResult,result,dept); 10 return result; 11 } 12 /* 13 * 这里主要使用递归加回溯的思想 14 */ 15 public void pathSum(TreeNode root,int K,List<Integer>currentResult,List<List<Integer>>result,int dept) { 16 if(root==null)return; 17 currentResult.add(new Integer(root.val)); 18 if(root.left==null&&root.right==null&&K==root.val+dept) { 19 result.add(new LinkedList(currentResult)); 20 }else { 21 pathSum(root.left,K-root.val-dept,currentResult,result,dept+1); 22 pathSum(root.right,K-root.val-dept,currentResult,result,dept+1); 23 } 24 currentResult.remove(currentResult.size()-1); 25 } 26 }
4.主函数

1 public class Main { 2 3 public static void main(String[] args) { 4 Scanner input = new Scanner(System.in); 5 System.out.print("输入K:"); 6 int K = input.nextInt(); 7 System.out.println("输入数组(以‘#‘结束,例如:5 3 7 9 null 11 2 4 -1 null null 2 -2 #)"); 8 List<String> list = new ArrayList<String>();//集合接收输入串 9 String cin = null; 10 while(!"#".equals((cin=input.next()))) { 11 list.add(cin); 12 13 } 14 //将集合转成字符串数组 15 String[] levelOrder = new String[list.size()]; 16 for(int i=0;i<=list.size()-1;i++) { 17 levelOrder[i] = list.get(i); 18 } 19 20 //从左到右构造二叉树,并寻找路径和等于K的路径 21 BuildTree tree = new BuildTree(); 22 TreeNode root = tree.create(levelOrder); 23 printTree(root,K,0); 24 } 25 26 public static void printTree(TreeNode root,int K,int dept) { 27 if(root==null)return; 28 PathSum pathSum = new PathSum(); 29 30 List<List<Integer>> result = pathSum.pathSumEntry(root, K,dept); 31 for (List resultList : result) { 32 System.out.println(resultList); 33 } 34 35 printTree(root.left,K,dept+1); 36 printTree(root.right,K,dept+1); 37 } 38 }
一开始我还以为这道题就是个简单的路径查找算题,采用递归加回溯算法分分钟钟就可以解决这道题,当我再仔细看题的时候,才知道这不是一道简简单单的回溯算法题。还有二叉树如何构建问题,一看到构建二叉树题,还是觉得简单,结果自己还是太嫩了!没错,这是笔者第一次做分层构造二叉树题,笔者的思考可以参考题目分析部分,这里有笔者的思考的部分过程。第一次做分层构造二叉树,所以花费了不少时间,考虑不周还望各位老师同学指点,如果大家有更好的分层构造二叉树想法,可以分享链接到评论区,比如可以直接父节点找子节点。
每日一囧,微笑面对生活,我是懂先森
标签:回溯 node 参数 集合 一个 数据 lis 解释 递归
原文地址:https://www.cnblogs.com/damon-dhc/p/13659367.html