【NLP】最小编辑距离最简明的解释方法

标签：特性   col   技术   不同   开始   ima   插入   替换   数组   

网上讲最小编辑距离的文章有很多，但是看了一大堆，讲明白的实在是很少。

最小编辑距离指的是字符串A转化为字符串B的最小编辑次数，允许的操作有插入，删除，替换。

先来说一下插入删除操作，比如有hello，helo俩个字符串，前一个字符串减去一个l和后一个加上一个l，其实是没有区别的。那么把这个操作统称为对一个字符串的删除就好了。

再来说一下替换操作，helo和halo，将e替换成a或者将a替换成e，其实都是没区别的。

既然如此，那么大家都在说dp做最小编辑距离，那怎么理解呢。先上图。

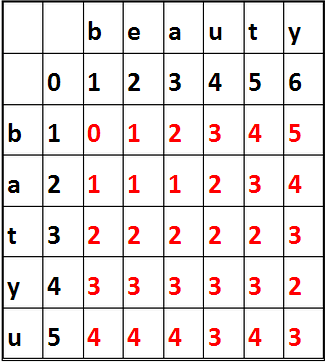
首先先说黑字部分。

首先一点是，如果双方字符串为空，那么最小编辑距离为0。如果有任意一方字符串不为空，那么最小编辑距离就为len(str(not_None_string))，这也是没问题的。

那么红字部分怎么来的呢，dp的一个特性就是当前状态由上一个状态决定。那么假设我要判断A[i:]和B[j:]的最小编辑距离，那么当前编辑距离是由上一个状态的最小编辑距离决定，也就是说在上一个状态需要修改最少多少次。上一个状态是有这么几种情况：

1.A[i-1:]与B[j]匹配需要修改K1次，如果此时加上了A[i]，那么就不匹配了，需要把A[i]去掉，操作数K1+1

2.同理，A[i:]与B[j-1:]匹配需要修改K2次，如果此时加上了B[j]，那么就不匹配了，需要把B[j]去掉，操作数K2+1

3.A[i-1:]与B[j-1:]匹配需要修改K3次，那么此时双方各加上A[i],B[j]，就要考虑了，如果俩个字符相同，那么操作数K3不变，如果字符不同，那么意味着要进行替换操作，不管谁替换谁都是K3+1

那么现在的状态就是上面三种情况取(K1+1,K2+1,K3+(0?1))最小的那个，换成矩阵中的状态转移方程为：

dp[i,j] = min(dp[i-1,j]+1,dp[i,j-1]+1,dp[i-1,j-1]+(0:1?A[i]==B[j]))

为什么要从0开始，因为从空字符串开始会更好算一点，黑框这些值不由dp状态生成，可以看成辅助计算的数组们。这个做法在很多需要二维矩阵的dp解法中都会运用到。多拿几道题练几遍就有思路了。

那么代码如下：

def func(s1,s2):
    edit = [[i+j for j in range(len(s2)+1)] for i in range(len(s1)+1)]
    for i in range(1,len(s1)+1):
        for j in range(1,len(s2)+1):
            if s1[i-1]==s2[j-1]:
                d=0
            else:
                d=1
            edit[i][j] = min(edit[i-1][j]+1,edit[i][j-1]+1,edit[i-1][j-1]+d)
    return edit[-1][-1]

其实这种解体思路也可以用在求一些二维的最短路径上，只不过生成的黑框不一样，解法还是一样的。

【NLP】最小编辑距离最简明的解释方法

标签：特性   col   技术   不同   开始   ima   插入   替换   数组   

原文地址：https://www.cnblogs.com/guangluwutu/p/13664306.html