标签:就是 网上 改变 cors 容量 ini 关于 为什么 details
前置技能:01分数规划, 最大权闭合子图
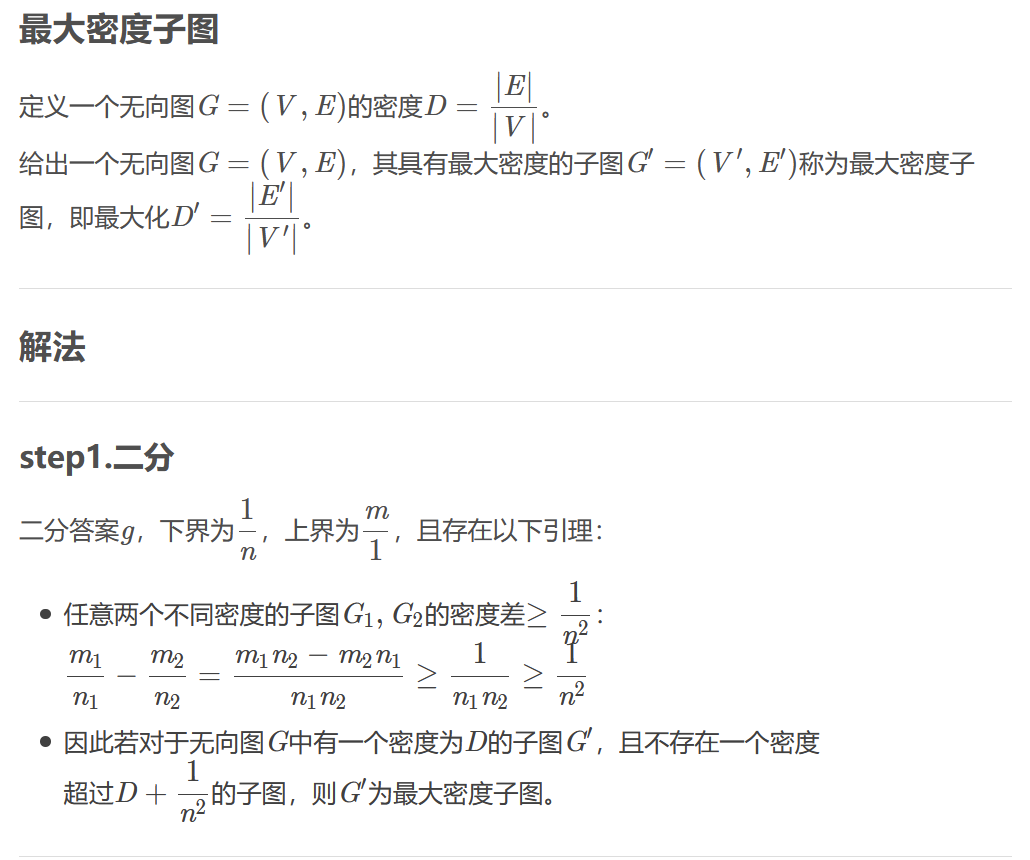


图片源自网上:https://blog.csdn.net/corsica6/article/details/88200297
因为我们假设g就是我们所求的最大值,那么有 E/ V <= g。之后我们移项一下就是E - gV了。
这一天是从上一条来的,上一条移项之后就是E - gV <= 0。
之后我们分析这个式子,如果选择一条边那么就一定会选其对应的点从而付出g或2g的代价。这不就是最大权闭合子图吗?
所以我们就可以建边了将每个点连向T,权为g代表需要付出g的代价。每条边抽象的点连向S权为1,代表的是收益。边对应的点连inf
之后就是最大权闭合子图 =(正向权相加)m - Dinic()。算是利用最大权闭合子图的性质来求E - gV,间接求得最大密度子图。
之后一旦不满足E - gV <= 0,即m - Dinic() > 0 那么说明g太小,所以是将左边界变大。
关于算法二:
一个显然的决策。。就是如果我们已经选定了一个点集,两点都在点集内的边一定要选。。。于是边数就可以看做(至少有一点在点集内的边)-(只有一点在点集内的边)
而(只有一点在点集内的边)相当于点集与其补集的最小割。。。
于是先转化最大化h(x)为最小化 -h(x)
也就是最小化(点数)* g - (至少有一点在点集内的边)+(只有一点在点集内的边)
也就是 (点数)* g - ((选的点的度数之和)/2 - 割)
把系数1/2给去掉。。就变成 2 (点数) g -((选的点度数之和) - 2 * 割)
于是建图就是。。

顺便一提推广的建图方式:
边带权:
边和点都带权: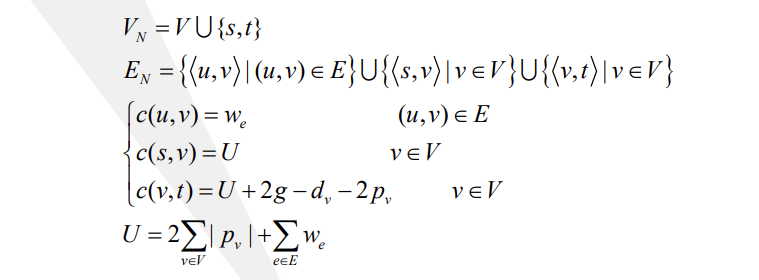
注意这里的c(u,v)建的是容量为w的双向边。
标签:就是 网上 改变 cors 容量 ini 关于 为什么 details
原文地址:https://www.cnblogs.com/Vikyanite/p/13672434.html