近期面试，有一题是用Python实现对图像卷积计算的加速实现，当时仅适用最暴力的方法-滑动窗口求内积，后来查找资料有转换成矩阵相乘和FFT的方法，特整理以记之。

基本概念

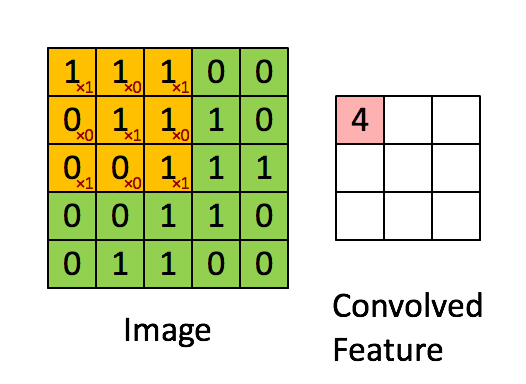
对图像（不同的数据窗口数据）和滤波矩阵（一组固定的权重：因为每个神经元的多个权重固定，所以又可以看做一个恒定的滤波器filter）做内积（逐个元素相乘再求和）的操作就是所谓的『卷积』操作，也是卷积神经网络的名字来源。

从数学公式看一下卷积和相关的定义：

相关： 其中 代表 的 复共轭（complex conjugate）

相关的计算步骤：

（1）移动相关核的中心元素，使它位于输入图像待处理像素的正上方

（2）将输入图像的像素值作为权重，乘以相关核

（3）将上面各步得到的结果相加做为输出

卷积：

卷积的计算步骤：

（1）卷积核绕自己的核心元素顺时针旋转180度

（2）移动卷积核的中心元素，使它位于输入图像待处理像素的正上方

（3）在旋转后的卷积核中，将输入图像的像素值作为权重相乘

（4）第三步各结果的和做为该输入像素对应的输出像素

Two-dimensional correlation is equivalent to two-dimensional convolution with the filter matrix rotated 180 degrees.

卷积计算中要把卷积核翻转180°，但在图像中大部分卷积核都是对称的，所以有些书籍和文章直接表示一致。

卷积计算--矩阵相乘

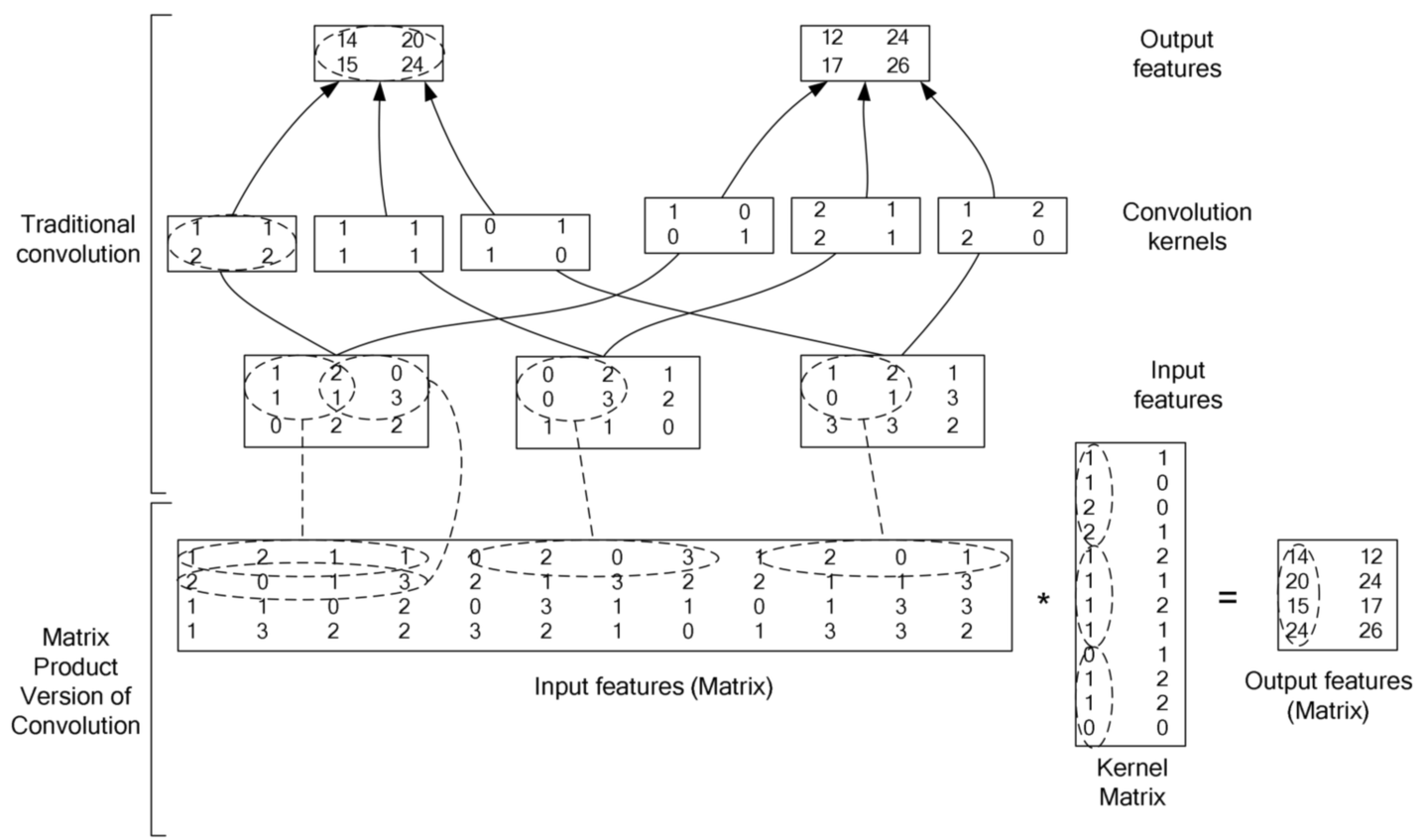
对于大的卷积核, 加速方法一般是使用傅里叶变换(或者其加强版: 快速傅里叶变换), 但是, 对于比较小的卷积核, 其转换到频域的计算量已经大于直接在空域进行卷积的计算量, 所以, 我们会发现在主流的深度学习框架中, 一般是直接在空域中进行卷积计算, 其加速计算的方法就是把卷积操作转换成矩阵相乘(因为有很多优化了的线性代数计算库和CUDA), 下面这张图充分说明了具体过程。

• 在上图中, input features每一个二维矩阵对应与 RGB 图像的 channel 或者是 feature map 中的channel。
• 目前常见的卷积都是 cross channel 的卷积, 既卷积核矩阵是 3 维的(width, height, depth), depth 的大小和feature map 的depth.(depth 就是有几张 feature map)。
• 3维卷积核的方法与 2 维的类似, 也是与 feature map 中相应的一个 3 维的矩阵对应位置元素相乘积。然后相加，2 维的卷积相当于 depth=1 的 3 维的卷

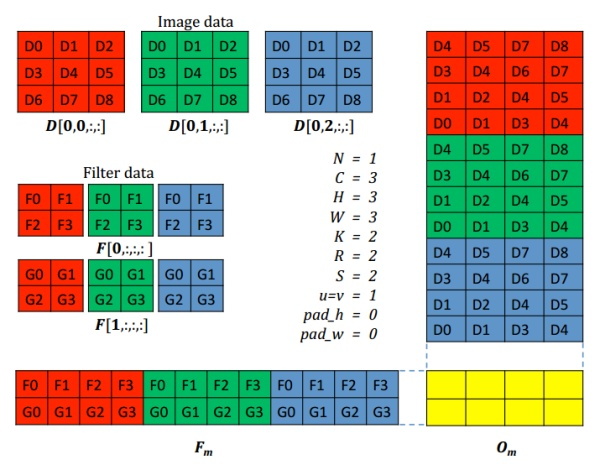
下图阐述了简单的二维卷积实现，输入图像是3*3的RGB数据，组成12*4的矩阵，3个2*2卷积核，卷积核组成2*12的矩阵，输出矩阵维度为2*4

卷积计算--FFT

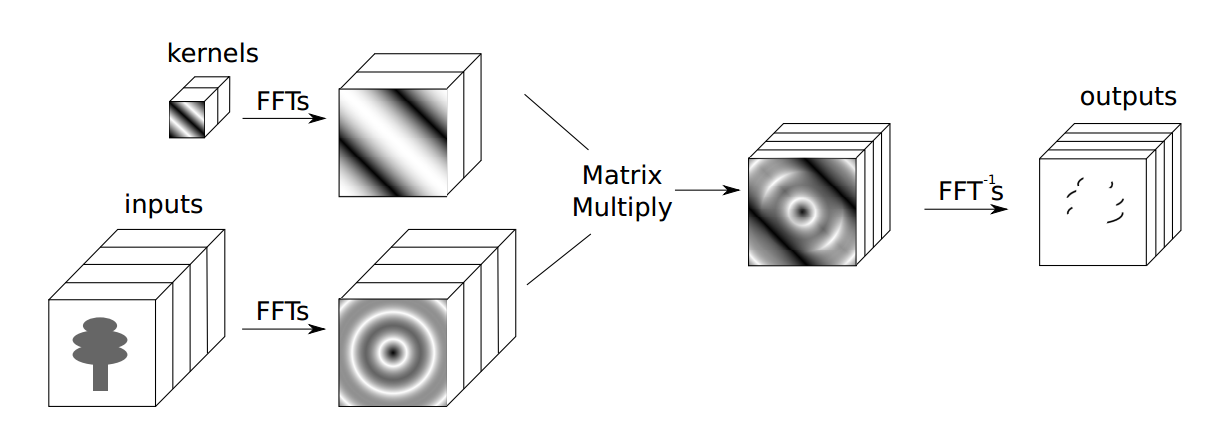
卷积定理表明，时域中的循环卷积相当于频域的点积。令F表示傅里叶变换F-1的倒数，我们可以计算函数f和g之间的卷积如下：

f ∗ g = F-1(F(f) · F(g))

通常，这种方法需要卷积核的尺寸大小接近输入图像的尺寸。对于卷积内核需要扩展到和Input一样大小，占用了大量内存，特别是CNN的前几层filter 大小远小于input大小。

参考文献

1、High Performance Convolutional Neural Networks for Document Processing

2、cuDNN_Efficient Primitives for Deep Learning

3、Fast training of convolutional networks through ffts