标签:https 控制 span table line 表示 cin ffffff 负数
最高位为符号位,0表示正数,1表示负数。
正数的原码:等于本身
负数的原码:等于(1-本身)
例如:X = +0.1011 , 原码 = 01011 ;
X = - 0.1011 , 原码 = 11011 ;(小数点可以保留或者省略)
最高位为符号位,0表示正数,1表示负数。
正数(X)的补码:等于本身。
负数(X)的补码:等于(2+X)=(2-|X|),(各位取反,末尾加一)
例如:X = +0.1011 , 补码 = 0.1011 ;
X = -0.1011 , 补码 = 1.0101 ;
正0的补码 = 负0的补码 = 0.0000 。
补码加法运算:[X+Y]的补码 = [X]的补码 + [Y]的补码 。
最高位为符号位,0表示正数,1表示负数。
正数(X)的反码 = 本身
负数(X)的反码 = 2 - (2的(-n)次幂)+ X , (各位取反)
例如:X = +0.1011 (n = 4), 反码 = 0.1011 ;
X = -0.1011 (n = 4) , 反码 = 1.0100 ;
正0的反码 = 0.0000 , 负0的反码 = 1.1111 ;
最高位为符号位,1表示正数,0表示负数。
正数(X)的移码 = 2的n次幂 + X的补码 = 符号位+本身 ;
负数(X)的移码 = X的补码 - 2的n次幂 = 符号位+(各位取反,末尾加一)
例如:X = +1011 , 补码 = 01011 , 移码 = 11011 ;
X = -1011 , 补码 = 10101 , 移码 = 00101 ;
注意:如果小数点后面有4位,则要进行右移4次,如果有6位,则要进行右移6次,依次类推。
在求部分积时,由于前一次部分积的最低位不再参与运算,因此可将其右移一位,相加数可直送而不必偏移,于是用N位加法器就可实现两个N位数相乘。
部分积右移时,乘数寄存器同时右移一位,这样可以用乘数寄存器的最低位来控制相加数(取被乘数或零0),同时乘数寄存器的最高位可接收部分积右移出来的一位,因此,完成乘法运算后,A寄存器中保存乘积的高位部分,乘数寄存器中保存乘积的低位部分。
(原码右移,最高位补0)(补码右移,最高位不变)
1.定点数原码一位乘法:
[X·Y]的原码 = [X]的原码 · [Y]的原码 = (符号位异或).(数值位两个数绝对值之积) 。
例题:
答案:X·Y = 0.10001111
解析:第一步:因为乘数的最后一位是1,所以部分积应该+X,得00.1101,然后进行右移一位,将最后移出的那一位变成乘数的首位,乘数也进行右移一位,最后一位移出丢失。
第二部:重复上面的步骤。
因为小数点后面有四位,所以共需要进行4此移位,4次加法,最后符号位进行异或,判断正负,得出结果。
注: (乘数的最后一位为1,部分积+X)
(乘数的最后一位为0,部分积+0)
2.定点补码一位乘法:
定点原码一位乘法用的是【原码】进行运算,例如+X是加的X的原码。
而定点补码一位乘法用的是【补码】进行运算,例如+X是加的X的补码。
注:在[X·Y]中,如果Y为负数,需要补充进行(-[X]的补码)操作;Y为正数,则不需要。
例如:

答案:[X·Y]的补码 = 0.10001111
解析:因为Y为负数,所以最后要进行加上 (-[X]的补码) 的操作。
3.布斯(Booth)公式:
乘数的 最后一位 - 前一位 = 0 ,则部分积 + 0 ;
乘数的 最后一位 - 前一位 = 1; 则部分积 + [X]的补码 ;
乘数的 最后一位 - 前一位 = -1;则部分积 + [-X]的补码 ;
最后一步不移位。
例如:

注意:如果小数点后面有4位,则要进行右移2次,如果有6位,则要进行右移3次,和定点一位乘法不同。
原码两位乘法规则:
| Y(i-1) | Y(i) | C | 操作 | 操作 |
| 0 | 0 | 0 | 部分积+0,右移2位 | 0->C |
| 0 | 0 | 1 | +X,右移2位 | 0->C |
| 0 | 1 | 0 | +X,右移2位 | 0->C |
| 0 | 1 | 1 | +2X,右移2位 | 0->C |
| 1 | 0 | 0 | +2X,右移2位 | 0->C |
| 1 | 0 | 1 | -X,右移2位 | 1->C |
| 1 | 1 | 0 | -X,右移2位 | 1->C |
| 1 | 1 | 1 | +0,右移2位 | 1->C |
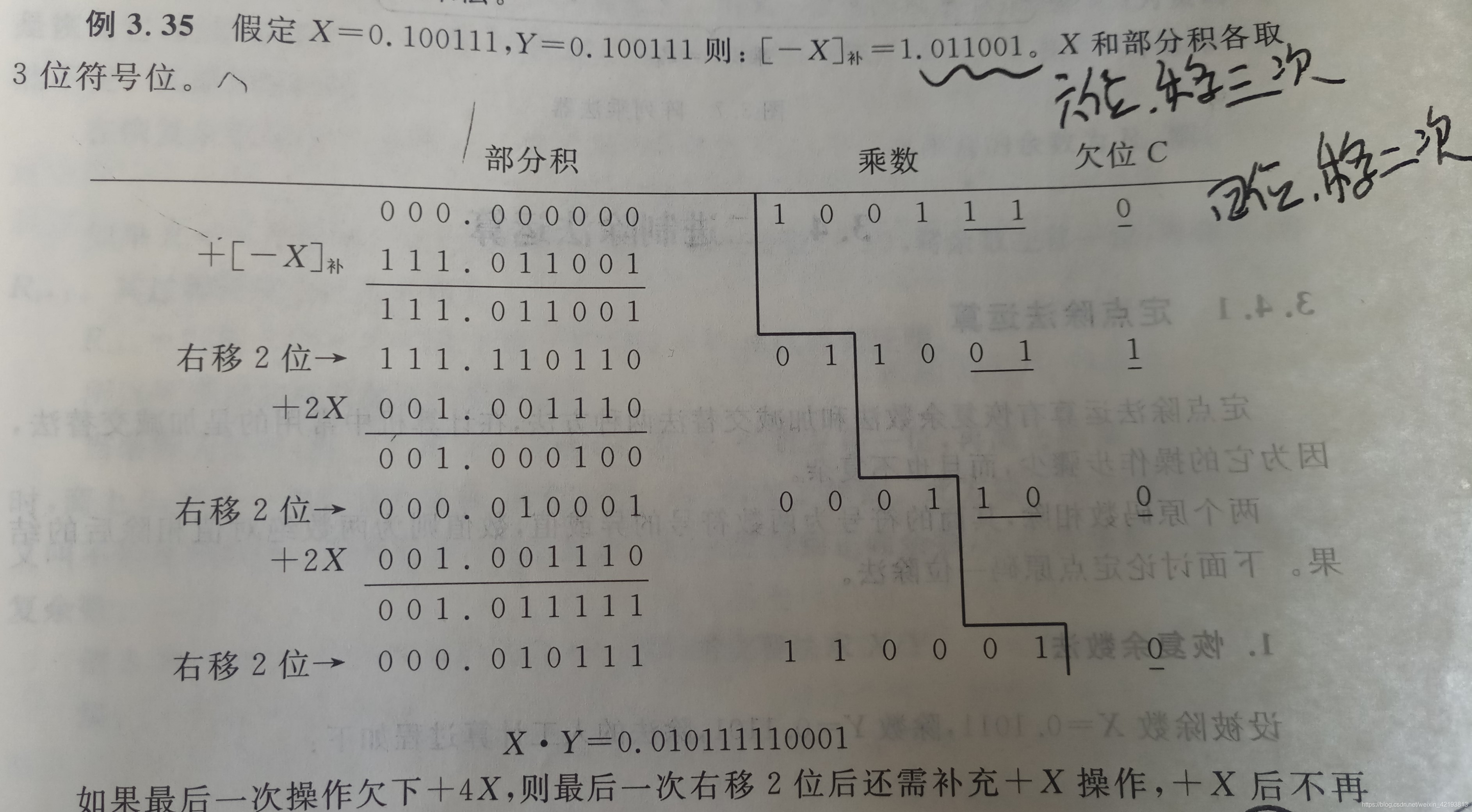
解析:第一次乘数的最后两位是11,而C的初始值是0,所以就是110,在上方表格中找到110,对应的操作是(-X,右移两位,C赋值为1),用补码来算,也就是+[-x]的补码,然后将C赋值为1,重复上面的操作。
(转)计算机组成与结构:原码、反码、补码、移码、二进制乘除法运算
标签:https 控制 span table line 表示 cin ffffff 负数
原文地址:https://www.cnblogs.com/caiyishuai/p/13689884.html