标签:algo 不用 cpp 返回 ima 答案 记录 找不到 code
线段树优化建图感觉是一种很妙的建图优化方法,可以给需要建边的题目的时间和空间带来极大的优化,于是想来大概总结一下(顺便弄两篇题解)
当我们遇到一道毒瘤题,要求我们对区间有交的一些点或一些区间之前进行连边的时候,我们最暴力的做法就是直接\(O(n^2)\)判断每个区间是否有交,并且给每一对有交的点连两条边,但是如果数据稍微大一些,例如出到了\(3e5\)的级别,毒瘤出题人就可以构造数据让你连出\(n^2\)条边,如果是一道\(2-SAT\)题目的话还需要进行tarjan进行缩点,这样的空间和时间复杂度一定是不能让我们接受的,但是我们是不是可以对于一堆点开一个源点,这个源点指向这一堆点,那么我们再想向这一堆点的时候就直接和源点连上就可以了?这样貌似就可以对于时空都有很大的优化,于是线段树优化建图的思想就诞生了。
前面提到,题目要求我们判断区间是否有交,处理区间问题的数据结构,我们不难想到线段树。我们可以存下来每个区间的左右端点,对其进行离散化,就可以开出一棵以值域为下标的线段树,我们就可以把每个节点所代表的区间都"拍"在这棵线段树上,放几张从luogu弄来的图片 来源链接
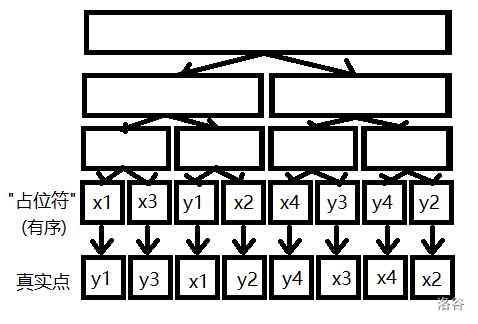
比如上图,在建树的时候我们需要把父节点向它的每一个儿子连一条边,来方便我们区间连边.假设最底层的节点从左到右依次表示的区间为\(1\)到\(8\)(离散化之后的区间),假设我们现在有一个区间为\(2\)到\(5\)的节点,我们就可以把这个区间分为\(3\)段,分别放在表示\([2,2]\),\([3,4]\),\([5]\)的三个区间上(可以开一个vector存一下),在假设现在有一个区间为\(3\)到\(4\),我们显然需要把这两个点连起来,我们不需要知道在区间\([3,4]\)上有哪些点直接把这个点和树上代表区间\([3,4]\)的节点连起来就行了,在我们之前在树上连的边的帮助下这个节点就和值域区间在这个节点及其儿子的所有节点都连了起来,是不是很方便?再放一张图帮助理解一下.(还是从luogu弄的)
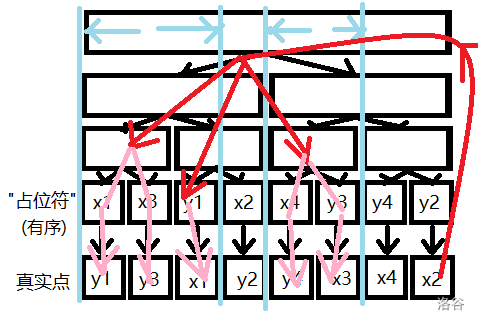
通过读题我们发现出题人要求我们对于一个炸弹都向它可以炸到的其他炸弹连一条边,然后我们跑tarjan缩点,再统计每个点能抵达的节点权值和就可以了,(是不是很简单),再看一下数据范围\(n≤500000\),如果出题人让\(n\)个炸弹都可以彼此炸到,那么我们就连出来了\(n^2\)条边,直接凉凉.但是我们发现每个炸弹都有一个值域区间,于是我们似乎可以考虑把每个炸弹的位置作为下表开出线段树(当然要离散化),此时的每个叶子就可以代表相应的炸弹,从每个炸弹出发,我们可以二分出它可以炸到的最左边的炸弹和最右边的炸弹,这个在线段树上是一个区间,我们就可以用线段树优化这个建图过程.之后我们需要求出每个点能抵达的节点权值和,这个东西其实我们只用求出该炸弹可以炸到的最左和最右的炸弹编号,大的减小的就行了,所以我们在缩点的时候就要记录一下该联通块里面位置最左边和最右边的节点编号,方便最后dfs的时候统计答案.这样就可以通过这到紫题了.
上代码:
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
typedef long long ll;
#define mid ((l + r) >> 1)
const int N = 1e6 + 10;
const int Mod = 1e9 + 7;
std::vector<int> edge[N], ve[N];
struct Tree {
int lson, rson, l, r;
} tree[N];
int sum, id[N];
ll tl[N], tr[N]; //存每个线段树节点的左右端点
void build(int &t, int l, int r) {
if(!t) {
t = ++sum;
}
tree[t].l = l;
tree[t].r = r;
if(l == r) {
id[l] = t;
tl[t] = tr[t] = l;
return;
}
build(tree[t].lson, l, mid);
build(tree[t].rson, mid + 1, r);
edge[t].push_back(tree[t].lson);
edge[t].push_back(tree[t].rson);
tr[t] = tr[tree[t].rson];
tl[t] = tl[tree[t].lson];
}
void change(int t, int cl, int cr, int id) {
int l = tree[t].l, r = tree[t].r;
if(cl <= l && r <= cr) {
edge[id].push_back(t);
return;
}
if(cr <= mid) change(tree[t].lson, cl, cr, id);
else if(cl > mid) change(tree[t].rson, cl, cr, id);
else {
change(tree[t].lson, cl, cr, id);
change(tree[t].rson, cl, cr, id);
}
}
ll x[N], r[N];
int dfn[N], low[N], dfn_cnt, scc_cnt, belong[N];
ll L[N], R[N]; //存储每个联通块里面的最左和最右端点的编号.
int top, sta[N], root;
void tarjan(int u) {
dfn[u] = low[u] = ++dfn_cnt;
sta[++top] = u;
for(int i = 0; i < edge[u].size(); ++i) {
int v = edge[u][i];
if(!dfn[v]) {
tarjan(v);
low[u] = std::min(low[u], low[v]);
}
else if(!belong[v])
low[u] = std::min(low[u], dfn[v]);
}
if(dfn[u] == low[u]) {
scc_cnt++;
int t;
do {
t = sta[top--];
belong[t] = scc_cnt;
L[scc_cnt] = std::min(L[scc_cnt], tl[t]); //比较更新最值
R[scc_cnt] = std::max(R[scc_cnt], tr[t]);
}while(t != u);
}
}
int vis[N];
void dfs(int u) { //最后一遍dfs求出每个炸弹能炸到的最左和最右的炸弹编号
vis[u] = 1;
for(int i = 0; i < ve[u].size(); ++i) {
int v = ve[u][i];
if(vis[v]) {
L[u] = std::min(L[u], L[v]);
R[u] = std::max(R[u], R[v]);
continue;
}
dfs(v);
L[u] = std::min(L[u], L[v]);
R[u] = std::max(R[u], R[v]);
}
}
int main() {
memset(L, 0x7f, sizeof(L));
int n;
scanf("%d", &n);
for(int i = 1; i <= n; ++i) {
scanf("%lld%lld", &x[i], &r[i]);
} //由于炸弹编号递增,不用sort + unique
build(root, 1, n);
for(int i = 1; i <= n; ++i) { //查找该炸弹能炸到的区间
int L = std::lower_bound(x + 1, x + n + 1, x[i] - r[i]) - x;
int R = std::upper_bound(x + 1, x + n + 1, x[i] + r[i]) - x;
if(x[R] > x[i] + r[i]) R--;
change(root, L, R, id[i]);
}
for(int i = 1; i <= sum; ++i) {
if(!dfn[i]) tarjan(i);
}
for(int i = 1; i <= sum; ++i) {
for(int j = 0; j < edge[i].size(); ++j) {
int v = edge[i][j];
if(belong[i] == belong[v]) continue;
ve[belong[i]].push_back(belong[v]);
}
}
for(int i = 1; i <= scc_cnt; ++i) {//缩点
if(!vis[i]) dfs(i);
}
ll res = 0;
for(int i = 1; i <= n; ++i) { //统计答案
int now = belong[id[i]];
res += 1ll * i * (R[now] - L[now] + 1);
res = res % Mod;
}
printf("%lld\n", res);
return 0;
}
和普通的线段树优化建图相比,这类问题需要注意的是即使一个点和它所代表的反点有交,也不能把这两个点连在一起,因为\(2-SAT\)的边表示的是选了边连出的节点,则必须选边连入的节点,而我们选了一个点就必须选它的反点....怪怪的
于是对于像上面的炸弹一样每个节点只对应一个叶子的情况,假设我们要想\([l,r]\)连边,反点在\(mid\)则我们可以把区间分为\([l,mid-1]\),\([mid+1,r]\)两个区间进行连边就可以了,但是这样处理在下面这道题里面就不适用了.(其实最初就是想写这道题的题解才有了这篇博客)
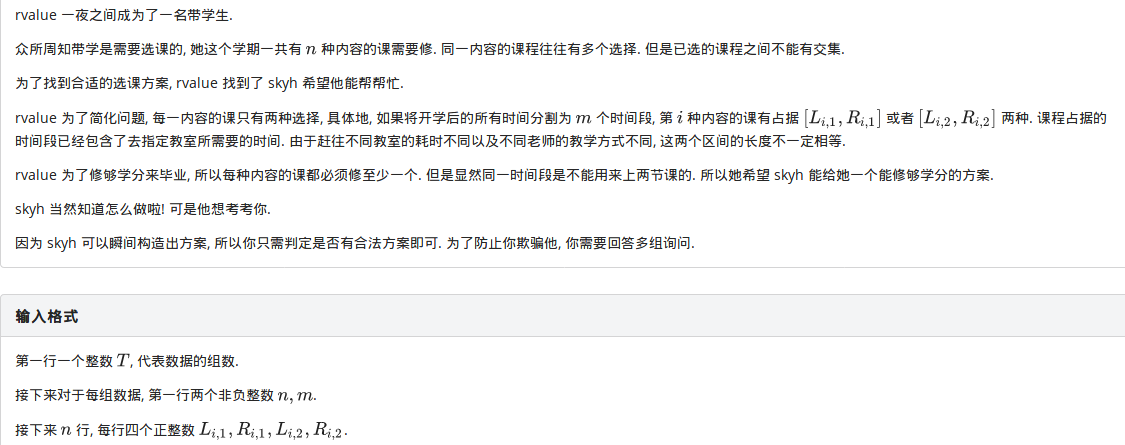
这道题多个区间相互限制,每种课必须选至少一个(当然我们直选一个就行),这一看就是一个\(2-SAT\)问题(然而考场上没能看出来),于是暴力连边就可以取得\(80\)左右的好成绩(然而考场上靠爆搜和剪枝甚至有水过的).于是我们考虑如何优化我们的建图过程.由于这道题每个节点都对应一个区间,再用一个叶子表示一个点就不再适用了.于是我们需要考虑一种新的建图方式
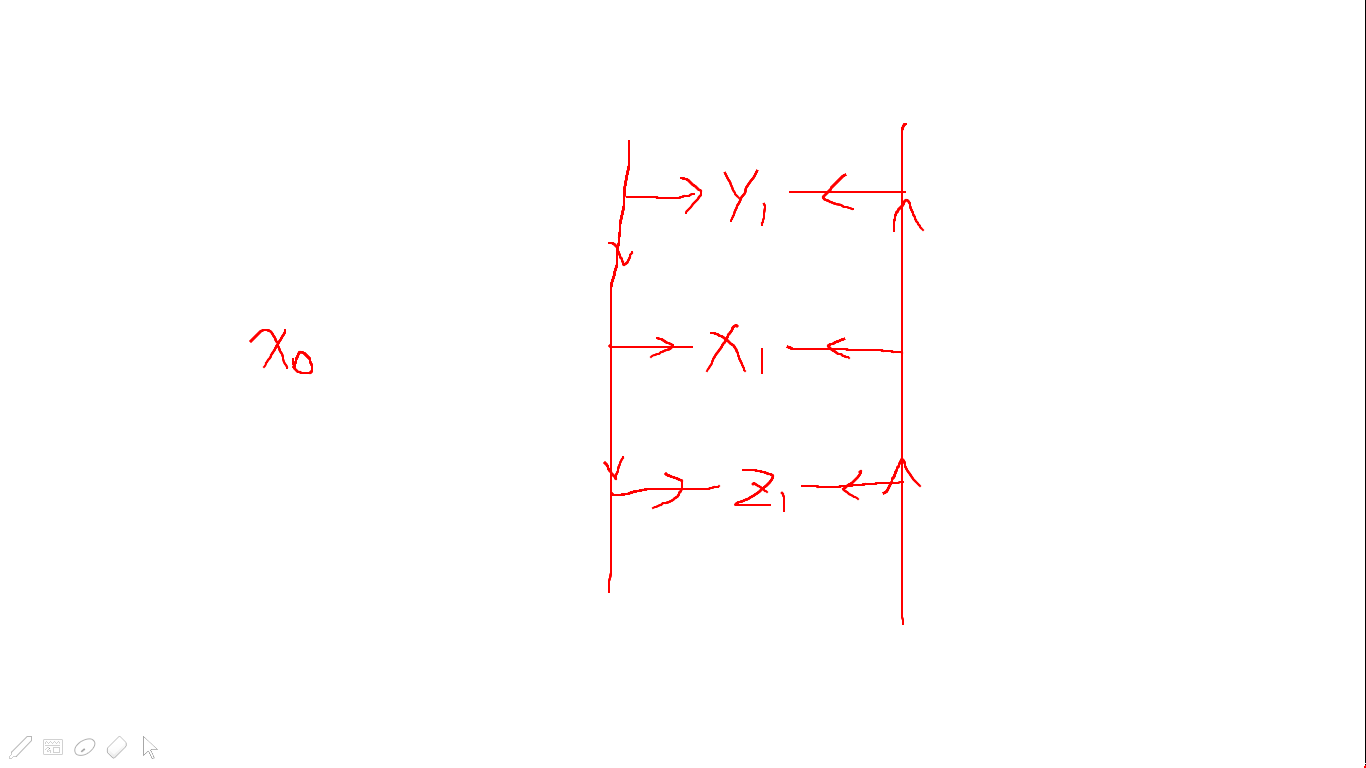
例如图中的\(x_0\)想要和右面的区间进行连边,而右面有存在该死的反点\(x_1\),我们需要避免这个问题,我们就多开了两条链来辅助我们进行连边优化,就是图中右面的节点两边的边,在两条链上又都有多个节点,和我们需要连边的节点连在一起(如图所示).那么我们连边时就可以这样连
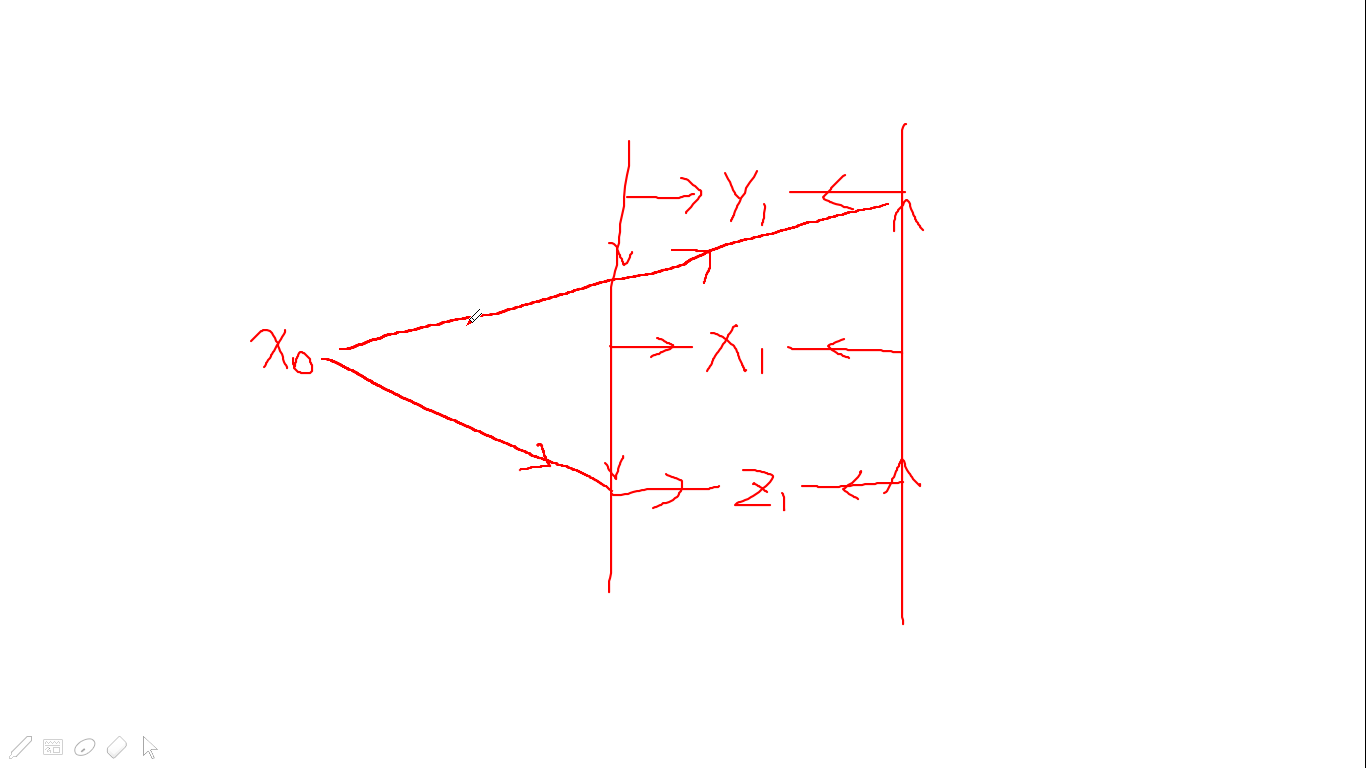
我们发现\(x_0\)完美的避开了自己的反点节点和区间里面的反点连在了一起.(说了这么多你线段树哪), 对于每一个树上的节点都开一条链,把他们连在一起.于是就有了...
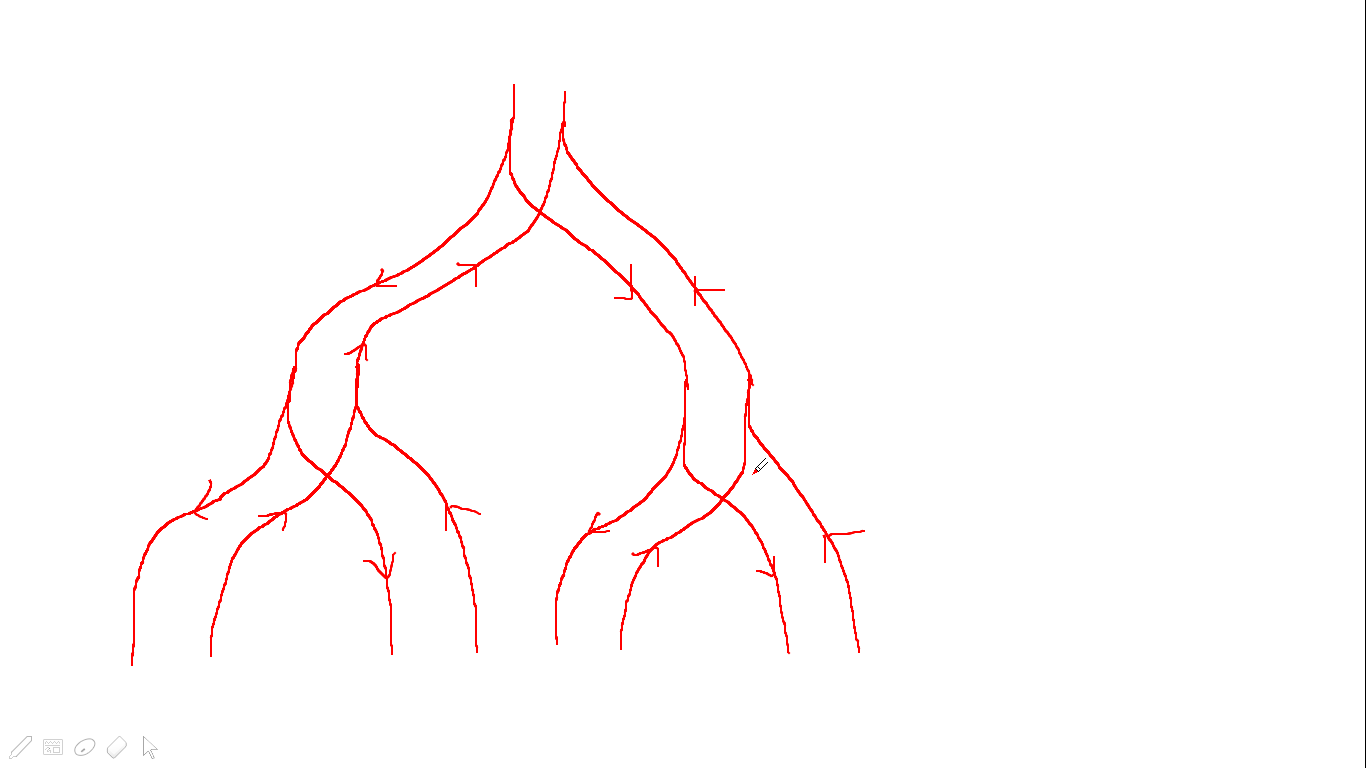
(很丑对不对,我也这么觉得)
我们就可以用线段树优化建图来干掉这道题了,由于一个区间和另一个区间有交在树上反映为所代表的两个节点相同或存在祖先关系,于是和上一道题不同,我们需要向上和向下都连出一条边,当我们把一个区间拍在树上的时候一个点的区间存的是其反点的编号.这样一个区间和该区间有交的时候连接的就是该点的反点了(符合普通\(2-SAT\)的连边方法).之后我们再对于每一个节点向自己对应的区间连边就行了,因为在拍反点的时候已经处理好了该区间在树上都存在于那些点,以及左边下一个节点和右边下一个节点的编号,我们再连边的时候直接把该节点和这些点连在一起就可以了.注意初始化的时候需要用\(for\)循环,不能用\(memset\),因为线段树优化建图特别烧内存,数组开的大,你会死在初始化里面(有兴趣的可以去题库看一下我因为这个问题\(T\)了多少次,改过来之后快了不止一点),于是这道题就做完了,代码并没有想象中的长.
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#define reg register
using std::lower_bound;
using std::upper_bound;
int read() {
int s = 0, f = 1;
char ch = getchar();
while(ch < ‘0‘ || ch > ‘9‘) {
if(ch == ‘-‘) f = -1;
ch = getchar();
}
while(ch >= ‘0‘ && ch <= ‘9‘) {
s = (s << 1) + (s << 3) + (ch ^ 48);
ch = getchar();
}
return s * f;
}
#define lson (t << 1)
#define rson (t << 1 | 1)
#define mid ((l + r) >> 1)
const int N = 6e6 + 10;
struct Node {
int next, to, dis;
} edge[N];
int Head[N], tot, n, m;
void Add(int x, int y) {
edge[++tot].to = y;
edge[tot].next = Head[x];
Head[x] = tot;
}
std::vector<int> ve[N];
void add(int t, int l, int r, int al, int ar, int id) {
if(al <= l && r <= ar) {//把区间拍在节点上,注意id是反点编号
ve[t].push_back(id);
return;
}
if(ar <= mid) add(lson, l, mid, al, ar, id);
else if(al > mid) add(rson, mid + 1, r, al, ar, id);
else {
add(lson, l, mid, al, ar, id);
add(rson, mid + 1, r, al, ar, id);
}
}
using std::pair;
using std::make_pair;
#define x first
#define y second
int top;
std::vector<pair<int, int> > bel[N];//存储该点左右辅助节点编号,方便查找
void build(reg int t,reg int l,reg int r,reg int pre_l,reg int pre_r) {
reg int now_r = pre_r, now_l = pre_l; //构建上图的形状的线段树
for(reg int i = 0; i < ve[t].size(); ++i) {
reg int u = ve[t][i];
Add(++top, now_r);
now_r = top;
Add(now_l, ++top);
now_l = top;
Add(now_l, u);
Add(now_r, u);
bel[u].push_back(make_pair(now_l, now_r));
}
Add(now_l, ++top);//留一个‘线头‘
now_l = top;
Add(++top, now_r);
now_r = top;
if(l == r) {
return;
}
build(lson, l, mid, now_l, now_r);
build(rson, mid + 1, r, now_l, now_r);
}
int num[N], t;
int find_nxt(reg int pos,reg int u) { //查找该点左边下一个节点和右边下一个节点找不到
for(reg int i = Head[pos]; i; i = edge[i].next) { //返回-1,即到了线头的地方
if(edge[i].to != u) return edge[i].to;
else continue;
}
return -1;
}
int dfn[N], low[N], dfn_cnt, belong[N], scc_cnt, L[N], R[N];
std::stack<int> sta;
void tarjan(reg int u) {//常规tarjan
dfn[u] = low[u] = ++dfn_cnt;
sta.push(u);
for(reg int i = Head[u]; i; i = edge[i].next) {
reg int v = edge[i].to;
if(!dfn[v]) {
tarjan(v);
low[u] = std::min(low[u], low[v]);
}
else if(!belong[v]) {
low[u] = std::min(low[u], dfn[v]);
}
}
if(dfn[u] == low[u]) {
scc_cnt++;
reg int t;
do {
t = sta.top();
sta.pop();
belong[t] = scc_cnt;
}while(t != u);
}
}
void Init() {//初始化
dfn_cnt = 0;
scc_cnt = 0;
top = n * 2;
t = 0;
tot = 0;
while(!sta.empty()) sta.pop();
for(reg int i = 0; i < n * 20; ++i) {
ve[i].clear();
bel[i].clear();
Head[i] = 0;//千万不能memset!千万不能memset!千万不能memset!
belong[i] = 0;
dfn[i] = 0;
low[i] = 0;
}
}
void Solve() {
n = read();
m = read();
Init();
for(reg int i = 1; i <= n; ++i) {
L[i] = read();
R[i] = read();
L[i + n] = read();
R[i + n] = read();
num[++t] = L[i];
num[++t] = R[i];
num[++t] = L[i + n];
num[++t] = R[i + n];//存每个区间的位置,方便离散化
}
std::sort(num + 1, num + t + 1);
t = std::unique(num + 1, num + t + 1) - num - 1;
for(reg int i = 1; i <= n * 2; ++i) {
reg int l = lower_bound(num + 1, num + t + 1, L[i]) - num;
reg int r = upper_bound(num + 1, num + t + 1, R[i]) - num - 1;
add(1, 1, t, l, r, i > n ? i - n : i + n);//找该点拍在哪里
}
build(1, 1, t, ++top, ++top);//建出线段树
for(reg int i = 1; i <= n * 2; ++i) {
reg int nxt = i > n ? i - n : i + n;
for(reg int j = 0; j < bel[nxt].size(); ++j) {
if(~find_nxt(bel[nxt][j].x, nxt))//每个点向和自己有交的点连边,前提是有点
Add(i, find_nxt(bel[nxt][j].x, nxt));
if(~find_nxt(bel[nxt][j].y, nxt))
Add(i, find_nxt(bel[nxt][j].y, nxt));
}
}
for(reg int i = 1; i <= top; ++i) {
if(!dfn[i]) tarjan(i);
}
for(reg int i = 1; i <= n; ++i) {
if(belong[i] == belong[i + n]) {
puts("NO");//判断可行性
return;
}
}
puts("YES");
}
int main() {
freopen("class.in", "r", stdin);
freopen("class.out", "w", stdout);
reg int t = read();
while(t--) {
Solve();
}
return 0;
}
完结撒花...
标签:algo 不用 cpp 返回 ima 答案 记录 找不到 code
原文地址:https://www.cnblogs.com/li-jia-hao/p/13773651.html