标签：temp 概率 user 容错 中心 距离 个人 理解 loading
格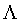
是m维欧式空间 Rm上确定的一组线性无关的向量的整数线性组合。格 L的基 B=b1,b2,…bn∈Rm×n，其中的每个分量线性无关。
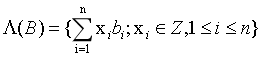
同一个格可以由不同的格基表示。m 称为格的维数，n称为格的秩。满足 m = n 的格称为满秩的，通常我们只考虑满秩的格。
对于格的任意一组基B，定义基本的平行六面体为：
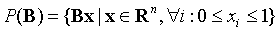
格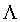
的对偶格定义为与格
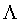上的向量具有整数内积
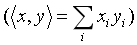的所有向量的集合，即
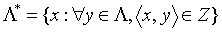
一个格的对偶格也是一个格，并且如果格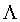
是由基B生成的格，则B*=(BT)-1是对偶格
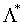的一个基，其中矩阵BT是矩阵B的转置矩阵。根据对偶格的对称性，可知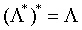
一个格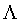
，它的一组基构成矩阵B，它的行列式
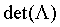定义为平行六面体Ρ(B)的体积，可通过下列等式求出：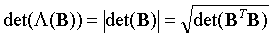
一个格的行列式是一个不变量，与格的基的选取无关。
令为秩为n的格，格的最短非零向量的长度表示为，也称为一个格的最小距离，是任意两个不同格点的最小距离，等于最短非零格向量的长度：
给定随机矩阵，其规模为较大的整数n和m，q为大素数，q模格为
个人理解*：中的向量x={x1,x2,x3,…,xm}，x满足Ax得到的n维向量中的每一个数xi mod q=0。是m维格。
和是m维格整数格，而且为对偶格。
定义1：对于任意向量c，x∈Rn和任意s>0，令，是以c为中心，参数为s>0的高斯密度函数。通常，当c=0，s=1时省略s和c。
因为，所有以c为中心，参数s>0的连续的高斯分布可以定义为其概率密度函数
()
从该分布中选择的向量与中心c的预期平方距离是，所以，可以被看认为是中心在c，半径为的球体。
定义2： 格上的离散高斯概率分布定义如下
密码学方案的安全性的一个重要条件是：底层的数学问题是困难的。格问题的经典困难问题有很多，如最短向量问题（SVP）、近似最短向量问题判定版本（GapSVP）、最近向量问题 (CVP)等等。
1996 年，Ajtai 给出了格中困难问题从最坏情况到平均情况的规约证明。密码学中的困难性需要的是在 "平均情况" 下的困难性。Ajtai 的工作使得基于格问题构造的密码方案具有了可证明安全的性质。新的格困难问题中，有几种重要的平均情况困难的问题：SIS、LWE、RLWE 及变种。
*最短向量问题(SVP)*：给定n维格基B。寻找格中的非零向量v，使得，即向量v是格中最短的向量。
*最近向量问题(CVP)*：给定n维格基B，目标向量t。寻找格中的非零向量v，使得向量v与目标向量t的距离最小，把这个最小距离记为。
*最短无关向量组问题(SIVP)*：给定n维格基B，有理数γ≥1。寻找格中的n个线性无关的格向量S，使得，其中是S中向量范数的最大值。
*小整数解问题(SIS)*：给定整数m、n和p，随机选取矩阵A∈Zqn×m和界定参数 β，求解非零整数向量 z∈Zm\0，使得 Az = 0 mod q ，且 。
*容错学习问题 ( LWE)*：给定均匀随机生成的矩阵 A∈Zqn×m ,s∈Zqn和s∈Zqm服从分布 ， 。A搜索版本的 LWE 问题（Search LWE）为：给定多组 (Ai,bi)，找到 s，一般在密钥交换中bi作为公钥，s作为私钥，ei是不公开的部分。。定版本的 LWE 问题（Decision LWE）为：将bi和均匀随机生成的向量区分开。
*环上容错学习问题 (RLWE)*：给定均匀随机生成的多项式 a∈Rq，s∈Rq和 e∈Rq 服从分布 ，。搜索版本的 RLWE 问题 (Search RLWE) 为：给定多组 （ai,bi），找到s。判定版本的 RLWE 问题 (Decision RLWE) 为：将bi和均匀随机生成的向量区分开。
标签：temp 概率 user 容错 中心 距离 个人 理解 loading
原文地址：https://www.cnblogs.com/2499mly/p/13774318.html
