标签：技术 alt str 二次 例子 sci font 数值 height
定义
函数
是凸的，如果dom f是凸集，且对于任意
和任意
，有
从几何意义上看，上述不等式意味着点(x,f(x))和(y,f(y))之间的线段，在函数f的图像上方（如下图）
一阶条件
假设f可微（即其梯度
在开集dom f内处处存在），则函数f是凸函数的充要条件是dom f是凸集并且对于任意
，下式成立
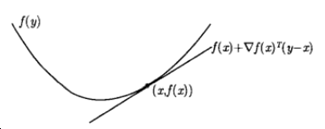
由
得出的仿射函数y即为函数f在点x附近的Taylor近似，对于一个凸函数，其一阶Taylor近似实质上是原函数的一个全局下估计。反之，如果某个函数的一阶Taylor近似总是其全局下估计，那么这个函数是凸的。
从一个凸函数的局部信息（即它在某点的函数值及导数），我们可以得到一些全局信息（如它的全局下估计）。这也许是凸函数的最重要的信息，由此可以解释凸函数以及凸优化问题的一些非常重要的性质。
证明：假设n=1，证明可微函数
是凸函数的充要条件是对于dom f内的任意x和y，有
首先假设f是凸函数，且
，因为dom f是凸集（某个区间），对于任意
，我们有
，由函数f的凸性可得
将上式两端同除t可得
令
，可以得到不等式
二阶条件
假设函数f二阶可微，即对于开集dom f内任意一点，它的Hessian矩阵或者二阶导数
存在，则函数f是凸函数的充要条件是，其Hessian矩阵是半正定阵：即对于所有的
，有
正定矩阵：给定一个大小为n×n的实对称矩阵A，若对于任意长度为n的非零向量x，有
恒成立，则矩阵A是一个正定矩阵
半正定矩阵：给定一个大小为n×n的实对称矩阵A，若对于任意长度为n的向量x，有
恒成立，则矩阵A是一个半正定矩阵
例子：二次函数
，其定义域为
，其表达式为
其中P为对称矩阵，P和q都为向量，r为标量，对于任意x，
，所以函数f凸的，当且仅当
标签：技术 alt str 二次 例子 sci font 数值 height
原文地址：https://www.cnblogs.com/tamoxuan/p/13786015.html
