标签：imu margin imp node order table idt 分布 线性查找
这样没有必要吧？我可否直接用numpy的向量化操作，直接做到时间O(1)，空间O(n)?
最近在看graph embedding的一些东西，发现像node2vec在采样节点路径以及line中采样边的时候都用到了Alias方法，这里简单总结一下。
给定一个离散型随机变量的概率分布规律 ，希望设计一个方法能够从该概率分布中进行采样使得采样结果尽可能服从概率分布
想象随机事件依其概率的大小分布在一个长度为1的线段上。那么在线段中随机取一点，观察该点落在哪个事件对应的区间中，就取该区间对应的事件即可。 具体实现如下：
k显然先构造一个存储累积事件概率的数组时间复杂度为 ，每次进行线性查找的时间复杂度为
上面在通过累加的方式构造出累积事件概率数组后，我们可以发现该数组满足非递减有序，对于有序数组的查找很容易想到使用二分查找进行优化，使用二分查找后的时间复杂度为
现在介绍使用空间换时间优化的方法Alias。
Alias方法将整个概率分布压成一个 的矩形，对于每个事件
，转换为对应矩形中的面积为
。
通过上述操作，一般会有某些位置面积大于1某些位置的面积小于1。我们通过将面积大于1的事件多出的面积补充到面积小于1对应的事件中，以确保每一个小方格的面积为1，同时，保证每一方格至多存储两个事件。
维护两个数组accept和alias,accept数组中的accept[i]表示事件i占第i列矩形的面积的比例。 alias[i]表示第i列中不是事件i的另一个事件的编号。
在进行采样的时候，每次生成一个随机数 ,再生成一个随机数
，若
，则表示接受事件
i，否则，拒绝事件 返回
alias[i]
该算法对应的代码文章末，可以看到预处理alias table的时间复杂度仍为 ,而每次采样产生事件的时间复杂度为
。
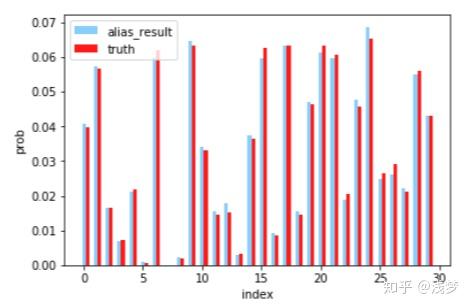N=30，k=10000的采样结果可视化展示
import numpy as np
def gen_prob_dist(N):
p = np.random.randint(0,100,N)
return p/np.sum(p)
def create_alias_table(area_ratio):
l = len(area_ratio)
accept, alias = [0] * l, [0] * l
small, large = [], []
for i, prob in enumerate(area_ratio):
if prob < 1.0:
small.append(i)
else:
large.append(i)
while small and large:
small_idx, large_idx = small.pop(), large.pop()
accept[small_idx] = area_ratio[small_idx]
alias[small_idx] = large_idx
area_ratio[large_idx] = area_ratio[large_idx] - (1 - area_ratio[small_idx])
if area_ratio[large_idx] < 1.0:
small.append(large_idx)
else:
large.append(large_idx)
while large:
large_idx = large.pop()
accept[large_idx] = 1
while small:
small_idx = small.pop()
accept[small_idx] = 1
return accept,alias
def alias_sample(accept, alias):
N = len(accept)
i = int(np.random.random()*N)
r = np.random.random()
if r < accept[i]:
return i
else:
return alias