标签：算法思路 形式 通过 平衡 最小值 概率 svm width com
支持向量机简述
算法思路：先研究在线性可分训练样本集上如何画出一条直线来分开，然后推广到非线性可分的问题上
如果存在一条直线可以分开圆圈和叉，那么在空间中一定存在着无数条直线可以分开圆圈和叉，那一条直线是最好的？
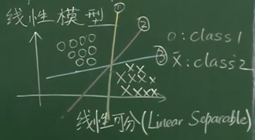
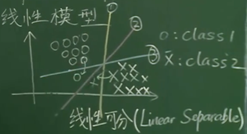
上图中，相比之下，2号线对于误差的容忍程度更多一些
将分界线平行的向两侧移动，直到接触到某个圆圈或叉为止，形成与分界线平行的两条直线，上述中的2号线是使得这两条线距离d最大的直线
将距离作为性能指标，且分界的直线需要在另外两条平行线的中间
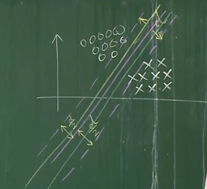
如果是一种不是最优的情况，此时d不是最大值
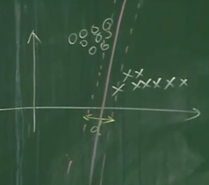
支持向量机的数学描述
支持向量机是一个最大化间隔的方法，将分界线向左移和向右移，与样本点交叉到的向量叫做支持向量
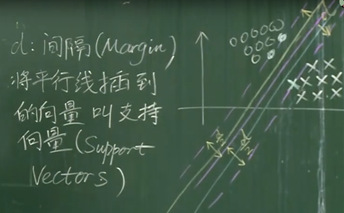
支持向量机算法只与支持向量有关，和其他向量没有关系，所以支持向量可以用在小样本的训练上，最终做出来的平行线只与支持向量有关
名词解释及定义：
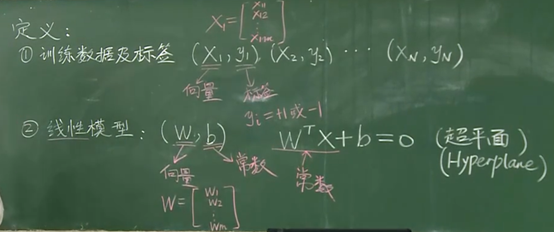
公式1
SVM标准形式：
SVM标准形式推导过程描述：
在
是支持向量的情况下，我们要让d最大
由于
与
表示同一个平面，所以缩放后
到平面的距离d不变，而
可以变为任意的值，这里让其为1
在所有的支持向量上
都等于1，而在其他不是支持向量的位置距离将会大于d
由于当前的w是定值，所以有
，所以最终的约束条件是
，结合标签y可以写成上述的限制条件
只要训练数据集是线性可分的，一定可以求出一个w和b
性质：
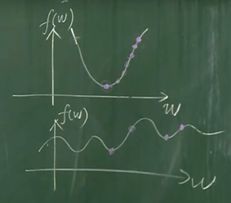
支持向量机将整个问题化成了一个凸优化的问题，在这个凸优化的问题上有一个全局最优的解
软间隔分类器
SVM的基本形态是一个硬间隔分类器，它要求所有样本都满足硬间隔约束（即函数间隔要大于1），所以当数据集有噪声点时，SVM为了把噪声点也划分正确，超平面就会向另外一个类的样本靠拢，这就使得划分超平面的几何间距变小，降低模型的泛化性能。除此之外，当噪声点混入另外一个类时，对于硬间隔分类器而言，这就变成了一个线性不可分的问题，于是就使用核技巧，通过将样本映射到高维特征空间使得样本线性可分，这样得到一个复杂模型，并由此导致过拟合（原样本空间得到的划分超平面会是弯弯曲曲的，它确实可以把所有样本都划分正确，但得到的模型只对训练集有效）。
为了解决上述问题，SVM通过引入松弛变量构造了软间隔分类器，它允许分类器对一些样本犯错，允许一些样本不满足硬间隔约束条件，这样做可以避免分类器过拟合，于是也就避免了模型过于复杂，降低了模型对噪声点的敏感性，提升了模型的泛化性能。
因为松弛变量时非负的，因此样本的函数间隔可以比1小。函数间隔比1小的样本被叫做离群点，我们放弃了对这些离群点的精确分类，这对我们的分类器来说是种损失，但是放弃这些点也带来了好处，那就是超平面不必向这些点的方向移动，因而可以得到更大的几何间隔（在低维空间看来，分类边界也更平滑）。显然我们必须权衡这种损失和好处。
松弛变量：松弛变量表示样本离群的程度，松弛变量越大，离群越远，松弛变量为零，则样本没有离群。样本点分类正确为零，如果分类有所偏差则对应一个线性的值，是总误差，这个值越小越好，越小代表对训练集的分类越精准
惩罚因子：惩罚因子表示我们有多重视离群点带来的损失，当C取无穷大时，会迫使超平面将所有的样本都划分正确，这就退化成了硬间隔分类器，当C趋于0时，我们不再关注分类是否正确，只要求间隔越大越好，那么我们将无法得到有意义的解且算法不会收敛
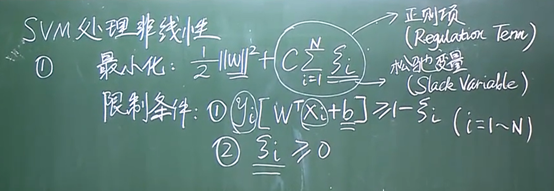
正则项使整个的目标函数变得规范化
其中C用来平衡两个部分最小值的权重，C的取值没有统一的概念，只是给C一个取值的范围，不断的去尝试那个C值更好
相比之下，SVM是一个好的方法，整个过程中需要取的参数只有一两个参数的组合，而对于神经网络等方法要尝试的参数会非常的多
核函数：
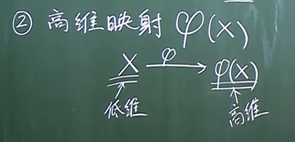
在低维空间里面线性不可分的数据集，到高维的空间里面将会以更大的概率线性可分
例子：
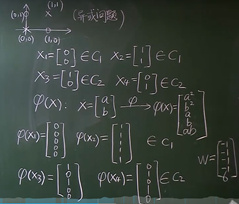
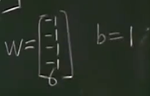
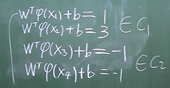
在无限维空间中线性可分的概率为1
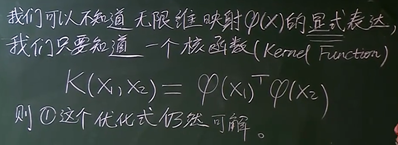
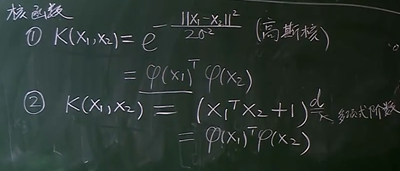
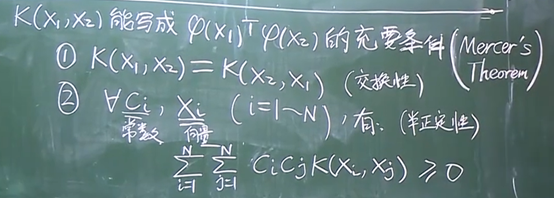
SVM对偶形式
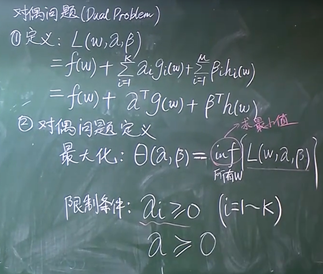
在限制α和β的前提下，去遍历所有的w，求解L的最小值（在遍历所有w的的情况下，求解L的最小值）
每确定一个α和β就能求出一个最小值，所以θ只与α和β有关
再针对所有的α和β求解θ的最大值
原问题与对偶问题的关系：
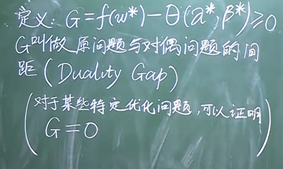
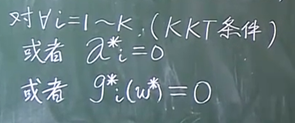
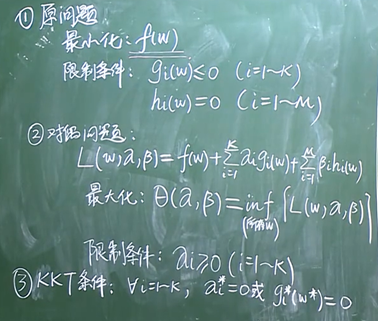
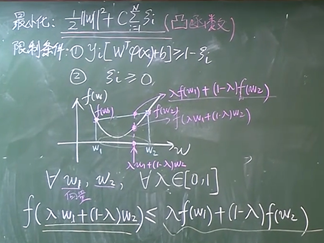
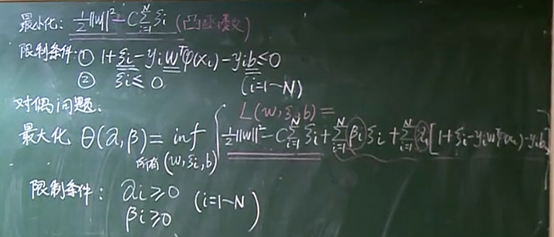
参数求解：
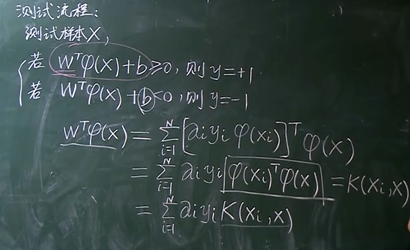
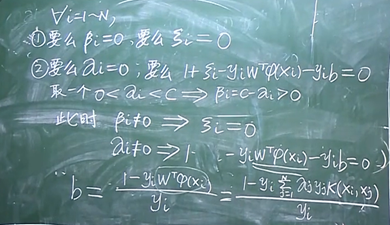
总结
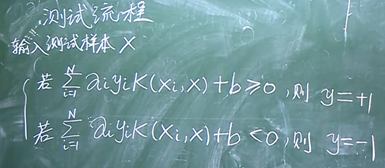
标签：算法思路 形式 通过 平衡 最小值 概率 svm width com
原文地址：https://www.cnblogs.com/tamoxuan/p/13829930.html
