A - 子集和问题

标签：数据   ret   inf   for   cst   img   using   问题   name   

Description

子集和问题的一个实例为〈S,t〉。其中，S={ x1 ， x2 ，…，xn }是一个正整数的集合，c是一个正整数。子集和问题判定是否存在S的一个子集S1，使得：

。
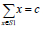
试设计一个解子集和问题的回溯法。
对于给定的正整数的集合S={ x1 ， x2 ，…，xn }和正整数c，计算S 的一个子集S1，使得：

。

Input

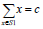
输入数据的第1 行有2 个正整数n 和c（n≤10000，c≤10000000），n 表示S 的大小，c是子集和的目标值。接下来的1 行中，有n个正整数，表示集合S中的元素。

Output

将子集和问题的解输出。当问题无解时，输出“No Solution!”。

Sample

Input

5 10
2 2 6 5 4

Output

2 2 6

题解：

递归回溯寻找子集，分为该数字在这个子集中和不在这个子集中两种情况。递归也是通过这两种情况进行的，但是注意“剪枝”，不然会超时。
而且这道题数据量十分大，就算剪枝也会超时。所以要多加一次判定。
另外这个题目可能存在多个解，然而数据偏弱，所以只要从第一个数据进行递归就能得到正解。其他解不用管。

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#define maxn 11234

using namespace std;

/**
*n集合大小
*k目标值
*s集合
*sum当前以累加值
*num当前子集的大小。
*flag标记是否已经找到子集。
*f记录当前子集。
*/
int s[maxn], k, n, sum, num, flag, f[maxn];

void slove(int i){
    //如果已经找到合适的子集，结束递归。
    if(flag){
        return;
    }
    int j;
    //累加。
    sum += s[i];
    //当前数据进入子集。
    f[num++] = s[i];
    //大于目标值，，剪枝，结束递归。
    if(sum > k)
        return;
    //已经找到合适的子集。
    else if(sum == k){
        flag = 1;
        return;
    }
    //继续还没达到目标值，继续累加。
    for(j=i+1; j<n; j++){
        slove(j);
        if(!flag){
            //说明当前数据不适合进入子集，回溯。
            sum -= s[j];
            num--;
        }
        else{
            return;
        }
    }
}

int main(){
    int i;
    scanf("%d%d",&n,&k);
    sum = 0;
    //计算子集所有数据相加能否达到目标值，没有这一步骤会超时。
    for(i=0; i<n; i++){
        scanf("%d",&s[i]);
        sum += s[i];
    }
    if(sum < k){
        printf("No Solution!\n");
        return 0;
    }
    sum = num = flag = 0;
    //开始进入递归。
    for(i=0; i<n; i++){
        slove(i);
        if(!flag){
            sum -= s[i];
            num--;
        }
        else{
            break;
        }
    }
    if(flag){
        for(i=0; i<num; i++){
            printf("%d%c", f[i], i==num-1 ? ‘\n‘ : ‘ ‘);
        }
    }
    else{
        printf("No Solution!\n");
    }
    return 0;
}

A - 子集和问题

标签：数据   ret   inf   for   cst   img   using   问题   name   

原文地址：https://www.cnblogs.com/luoxiaoyi/p/13854103.html