老年人的一些整理。。(复习用)
感觉现在队里数学一般见到都会做,就先不更数学的了。。
因为每次遇到计算几何的题都不敢开,这段时间就先搞这个吧。。
本文大量参考(几乎是搬运)了雅礼中学Hometown的ppt。。。
1.一般用一个数对\((x,y)\)来表示一个点或向量。
2.用一个点和一个向量来表示一个直线(或射线和线段)。
3.用一个直线可以表示一个半平面,即表示向量左边的半平面。。
1.向量 + 向量 : 两维坐标相加减即可。
2.向量 * 标量 : 两维坐标分别乘上标量。
1.\(a \cdot b\) \(=\) \(|a||b|\) \(cos\) \(\theta\)
2.设\(a\) \(=\) \((x_1,y_1)\) , \(b\) \(=\) \((x_2,y_2)\) ,则有 \(a \cdot b\) \(=\) \(x_1x_2+y_1y_2\)
1.\(a \times b\) \(=\) \(|a||b|\) \(sin\) \(\theta\)
2.设\(a\) \(=\) \((x_1,y_1)\) , \(b\) \(=\) \((x_2,y_2)\) ,则有 \(a \times b\) \(=\) \(x_1y_2-y_1x_2\)
3.几何意义表示的是以这两个向量为邻边构成的平行四边形的面积,当\(\theta < 0\) 时为正,否则为负。
4.可以用来判断向量的方向,对于向量 \(a,b\) ,若 \(a \times b > 0\) ,则 \(b\) 在 \(a\) 的逆时针方向。
1.把向量 \(a = (x,y)\) 逆时针转\(\theta\) ,得到的向量为 \(b = (x cos \theta - y sin \theta , x sin \theta + y cos \theta )\)
1.到直线距离:用向量叉积算出平行四边形的面积然后除以底边边长。。
2.到线段与射线距离:多讨论几种情况即可。
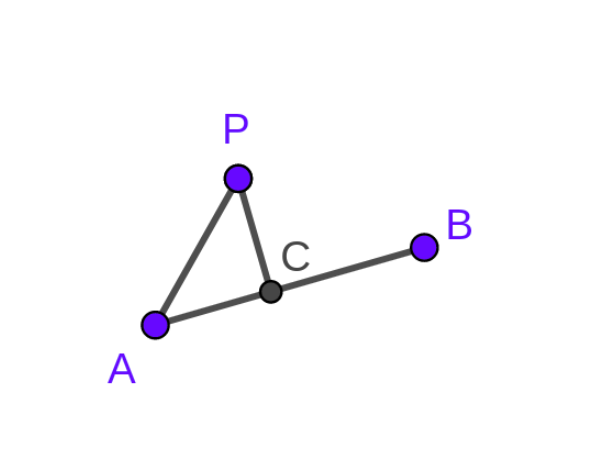
1.首先可以求出\(AP\) \(\cdot\) \(AB\) \(=\) \(|AC||AB|\) 和 \(AB\) \(\cdot\) \(AB\) \(=\) \(|AB||AB|\) 。
2.于是能求出\(\frac{|AC|}{|AB|}\) , 然后 \(C\) \(=\) \(A\) \(+\) \(AB \cdot \frac{|AC|}{|AB|}\)
1.对于各种几何形状,我们可以算出一个恰好覆盖了这个图形的矩形。
2.如果要判断两个图形是否相互包含或是相交等各种问题,可以先用这个矩形占据的位置快速判断一下,如果两个的矩形没有交,那肯定包含相交什么的都莫得了。
3.优点是判断很快,缺点是只能大致判断一下。。。
1.将问题简化为直线AB与直线CD相交时,求交点E。
2.通过叉积算出三角形ACD和三角形BCD的有向面积,然后根据比例算出E的坐标值。
1.线段与直线:若线段的两点在直线的同侧则不相交,否则相交。用之前叉积判断顺逆时针的方法判定点在直线的哪一侧即可。
2.线段与线段:做两次线段与直线的是否相交,两次都相交则两线段相交,否则不相交。
3.线段与射线:用线段与直线的方法做一遍,然后求一遍交点,判断交点是否在射线上。
1.这里介绍的是光线投射算法。
2.可以先用快速排斥判断一下,说不定能节省不少时间。
3.判断这个点是不是在多边形的角或边上。
4.然后我们从这个点出发,射出一条射线,然后跟多边形的所有线段判断是否相交,若相交次数为奇数,则在多边形内,否则在多边形外。
5.为了防止射线与多边形在角上相交,应将斜率设为一个无理数。
1.周长:直接算
2.面积:随便选一个辅助点\(O\),然后按顺时针或逆时针顺序枚举多边形上的点。计算\(OP_i\) \(\times\) \(O\)\(P_{i\% n + 1}\)得到有向面积,有向面积的总和的绝对值的1/2就是多边形的面积。
1.如果是平面上若干个离散的带权点的话,就能轻松算出重心了。公式:
\(X=(x1*m1+x2*m2+...+xn*mn)/(m1+m2+...+mn)\);
\(Y=(y1*m1+y2*m2+...+yn*mn)/(m1+m2+...+mn)\);
2.考虑把多边形转化成上面的形式,以第一个点为极点,然后和其余每相邻两个点求一次三角形有向面积以及三角形重心。
3.把这些三角形的重心当成离散的点,把对应三角形有向面积当成点的权值,就转化成了1的模型了。
1.选定一个辅助点,并以此为极坐标原点,然后按照角度来排序。。
例题 二人の星座
1.求点集的凸包(这个过水已省略。。)
例题1 Airport
例题2 妖怪
1.给定凸包\(A\)和\(B\),得到一个凸包\(C\),满足\({ \{ c|c=a+b,a \in A, b \in B \}}\),称\(C\)为\(A\)和\(B\)的闵可夫斯基和。
2.求闵可夫斯基和:首先可以将\(A\)和\(B\)的最最左下的点相加,显然这个点应该存在于\(C\)的凸包上。由于闵可夫斯基和的凸包上的每条边都应对应着原来两个凸包的边,所以直接将原来的边极角排序之后依次加上去。最后就得到了凸包\(C\)。
例题1 战争
1.动态插入点,并在过程中进行一些询问。(不支持既有插入又有删除的。。)
2.只有删除的话可以时间倒流变成插入。
3.具体做法就是用set维护一个极角序凸包,插入直接lower_bound找位置,然后按照一般凸包的规则删掉一些前驱和后驱。
4.维护极角序的凸包需要一个极点,这个极点可以在刚开始只有三个点的时候直接取三角形的重心。
例题1 Professor‘s task
原文地址:https://www.cnblogs.com/Yuigahama/p/13743798.html