标签:end etc 自动 指针 cep 记录 inline algorithm strong
回文自动机可以处理一个字符串的回文子串的信息,复杂度为 \(O(n)\)。
参考资料:翁文涛 《回文树及其应用》
回文自动机的每个节点代表一个回文子串,本质相同的回文子串在一个节点上。记节点 \(i\) 代表的回文串为 \(s_i\)(实现时不用记录),长度为 \(len_i\)。
回文自动机的结构可以看成两棵树,它们的根分别为 \(even\) 和 \(odd\),\(even\) 对应空回文串,\(odd\) 对应长度为 \(-1\) 的,实际上并不存在的回文串。
树上的一条边,也就是自动机的转移边对应一个字符。若 \(i\) 到 \(j\) 有一条对应字符 \(c\) 的转移边,则 \(s_j=cs_ic\),即在字符串前后各加一个 \(c\)。特别的,\(odd\) 经过一条边后得到单个字符。
与其它自动机类似,回文自动机的节点也有 \(fail\) 指针(失配指针 / 后缀链接),它指向这个节点最长的、不是自身的后缀回文串。特别的,\(fail_{even}=odd\)。通常记 \(fail_{odd}=odd\),虽然 \(odd\) 节点不可能失配(添加一个字符后成为单个字符,它一定是回文的)。
\(fail\) 指针显然构成一棵 \(fail\) 树。
下图来自于翁文涛的论文《回文树及其应用》。
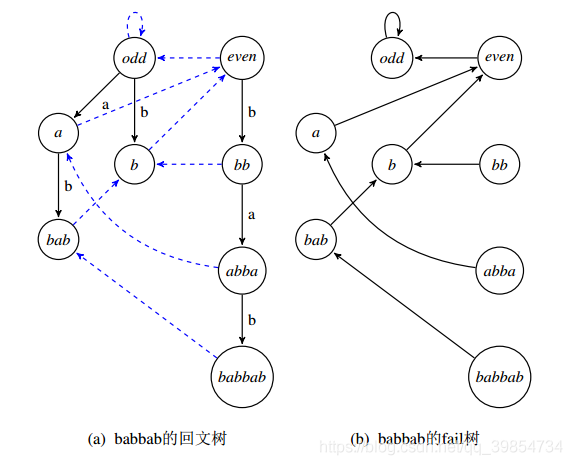
显然,若字符串 \(s\) 有 \(n\) 个本质不同的回文子串,状态数为 \(n+2\)。于是分析节点数即分析 \(s\) 本质不同的回文子串个数。下面是论文中的证明方法:
定理 3.1 对于一个字符串 \(s\),不同的回文子串个数最多只有 \(|s|\) 个。
证明 . 使用数学归纳法。
- 当 \(|s|=1\)时,只有 \(s[1\dots 1]\) 一个子串,并且他是回文的,所以结论成立。
- 当 \(|s| > 1\) 时,设 \(s = s‘c\),其中 \(c\) 为 \(s\) 的最后一个字符,并且结论对 \(s‘\) 成立。考虑以末尾字符 \(c\) 为结尾的回文子串,假设他们的左端点从左到右依次为 \(l_1,l_2,\dots,l_k\),那么由于\(s[l_1\dots |s|]\) 为回文串,那么对于所有的位置 \(l_1 \leq p \leq |s|\),都会有 \(s[p\dots|s|] = s[l_1\dots l_1+|s|-p]\),所以对于回文子串\(s[l_i\dots |s|]\),都会有 \(s[l_i\dots |s|]=s[l_1\dots l_1+|s|-l_i]\),当 \(i\neq 1\) 时,总会有\(l_1+|s|-l_i <|s|\),从而 \(s[l_i\dots |s|]\) 已经在 \(s[1\dots|s|-1]\) 中出现,因此每次不同的回文串最多新增一个,即 \(s[l_i\dots |s|]\)。因此结论对于 \(s\) 依然成立。
由数学归纳法可知定理 3.1 成立。
翻译一下就是:假如有多个以 \(c\) 结尾的回文子串,较短的那些肯定在最长的那个里面出现过至少一次。
因此状态数是 \(O(|s|)\) 的。由于每个状态只会有一个转移通向它、每个状态只会有一个 \(fail\),因此转移数也是 \(O(|s|)\) 的。
使用增量法。记录目前所在的节点 \(cur\) 指向目前字符串的最长回文后缀,初始值为 \(even\)。考虑新加入第 \(p\) 个字符 \(c\),显然由定理 3.1 可得,最多新增 1 个状态。我们反复跳 \(fail\) 来找到 \(s[p]=s[p-len_i-1]\),即该回文串再往前一个字符与新加的字符相等,显然最多跳到 \(odd\) 就找到了。假如找到的节点 \(x\) 没有对应的儿子 \(y\),新建一个节点:
将 \(cur\) 设为 \(y\),然后添加下一个字符。
由于 \(cur\) 的深度每次至多 \(+1\),因此时间复杂度是 \(O(|s|)\) 的(忽略字符集大小)。
代码:
/**********
Author: WLBKR5
Problem: luogu 5496
Name: 回文自动机
Source: 模板
Algorithm: 回文自动机
Date: 2020/06/05
Statue: accepted
Submission: https://www.luogu.com.cn/record/34145336
**********/
#include<bits/stdc++.h>
using namespace std;
int getint(){
int ans=0,f=1;
char c=getchar();
while(c>‘9‘||c<‘0‘){
if(c==‘-‘)f=-1;
c=getchar();
}
while(c>=‘0‘&&c<=‘9‘){
ans=ans*10+c-‘0‘;
c=getchar();
}
return ans*f;
}
const int N=5e5+10;
const int rt_1=1,rt0=0;
int ch[N][26],fail[N],cnt=2,cur=rt0;
int len[N],sz[N];
char s[N];
void init(){
len[rt_1]=-1; fail[rt_1]=0; //sz[rt_1]=1;
len[rt0]=0; fail[rt0]=rt_1; //sz[rt0]=1;
}
void extend(int pos,char c){
int p=cur;
while(s[pos-len[p]-1]!=c)p=fail[p];
if(!ch[p][c-‘a‘]){
int t=cnt++;
len[t]=len[p]+2;
fail[t]=fail[p];
while(s[pos-len[fail[t]]-1]!=c)fail[t]=fail[fail[t]];
fail[t]=ch[fail[t]][c-‘a‘];
sz[t]=sz[fail[t]]+1;
ch[p][c-‘a‘]=t;
}
cur=ch[p][c-‘a‘];
}
int main(){
scanf("%s",s+1);
int n=strlen(s+1);
init();
for(int i=1;i<=n;i++){
extend(i,s[i]);
printf("%d ",sz[cur]);
s[i+1]=(s[i+1]-97+sz[cur])%26+97;
}
return 0;
}
假如要求支持在字符串开头、结尾插入字符(LOJ #141.回文子串),一个简单的想法是维护 \(cur‘\) 与 \(fail‘\),分别代表当前字符串的最长回文前缀和各个节点的最长回文前缀。
考虑到回文串正着看、反着看都一样,实际上回文串的最长回文前缀,也就是其最长回文后缀。所以 \(fail‘=fail\),只维护 \(fail\) 即可。
在末尾(开头)插入字符时,只有整个串成=成为了一个回文串,\(cur‘\)(\(cur\))才会受影响。特殊处理这种情况。
模板题:LOJ #141.回文子串
代码:
/**********
Author: WLBKR5
Problem: loj 141
Name: 回文子串
Source: 模板
Algorithm: 回文自动机
Date: 2020/06/06
Statue: accepted
Submission: loj.ac/submission/826336
********/
#include<bits/stdc++.h>
using namespace std;
int getint(){
int ans=0,f=1;
char c=getchar();
while(c>‘9‘||c<‘0‘){
if(c==‘-‘)f=-1;
c=getchar();
}
while(c>=‘0‘&&c<=‘9‘){
ans=ans*10+c-‘0‘;
c=getchar();
}
return ans*f;
}
const int N=4e5+10;
const int rt_1=1,rt0=0;
int ch[N][26],fail[N],cnt=2,cur=rt0,ruc=cur;
int len[N],sz[N];
char s[N<<1];
char tmp[N];
int l=N,r=N-1;
void init(){
len[rt_1]=-1; fail[rt_1]=0; //sz[rt_1]=1;
len[rt0]=0; fail[rt0]=rt_1; //sz[rt0]=1;
}
long long ans=0;
void push_back(char c){
s[++r]=c;
int p=cur;
while(s[r-len[p]-1]!=c)p=fail[p];
if(!ch[p][c-‘a‘]){
int t=cnt++;
len[t]=len[p]+2;
fail[t]=fail[p];
while(s[r-len[fail[t]]-1]!=c)fail[t]=fail[fail[t]];
fail[t]=ch[fail[t]][c-‘a‘];
sz[t]=sz[fail[t]]+1;
ch[p][c-‘a‘]=t;
}
cur=ch[p][c-‘a‘];
if(len[cur]==r-l+1)ruc=cur;
ans+=sz[cur];
}
void push_front(char c){
s[--l]=c;
int p=ruc;
while(s[l+len[p]+1]!=c)p=fail[p];
if(!ch[p][c-‘a‘]){
int t=cnt++;
len[t]=len[p]+2;
fail[t]=fail[p];
while(s[l+len[fail[t]]+1]!=c)fail[t]=fail[fail[t]];
fail[t]=ch[fail[t]][c-‘a‘];
sz[t]=sz[fail[t]]+1;
ch[p][c-‘a‘]=t;
}
ruc=ch[p][c-‘a‘];
if(len[ruc]==r-l+1)cur=ruc;
ans+=sz[ruc];
}
int main(){
scanf("%s",tmp+1);
int n=strlen(tmp+1);
init();
for(int i=1;i<=n;i++)push_back(tmp[i]);
int q=getint();
while(q--){
int op=getint();
if(op<=2){
scanf("%s",tmp+1);
int n=strlen(tmp+1);
for(int i=1;i<=n;i++)(op==1?push_back:push_front)(tmp[i]);
}
if(op==3){
printf("%lld\n",ans);
}
}
return 0;
}
更高深的技术(如支持删除字符、可持久化 etc.)就不写了(其实是看不懂)。
标签:end etc 自动 指针 cep 记录 inline algorithm strong
原文地址:https://www.cnblogs.com/wallbreaker5th/p/13905622.html