标签:http rgba src loading 观察 假设 没有 data color
给定一个包含 0 和 1 的二维网格地图,其中 1 表示陆地 0 表示水域。
网格中的格子水平和垂直方向相连(对角线方向不相连)。整个网格被水完全包围,但其中恰好有一个岛屿(或者说,一个或多个表示陆地的格子相连组成的岛屿)。
岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
示例 :
输入:
[[0,1,0,0],
[1,1,1,0],
[0,1,0,0],
[1,1,0,0]]
输出: 16
解释: 它的周长是下面图片中的 16 个黄色的边:
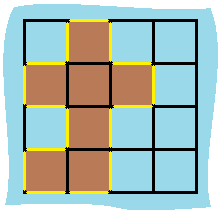
————————————————————————————————————————————————————————————————————————————————————————————
岛屿问题是一类经典的网格搜索类问题。
Q1:如何在网格上做DFS
M * N大小的网格,网格中的每一个小方格和其四周四个方格相邻(当然存在边界情况),接下来是具体操作步骤:
Step 1: 每个方格与其上下左右的四个方格相邻,则 DFS 每次要分出四个岔:
void Create_DFS(int[][]grid,int r,int c){//row and column DFS_G(grid,r-1,c); //上相邻 DFS_G(grid,r+1,c); //下相邻 DFS_G(grid,r,c-1); //左相邻 DFS_G(grid,r,c+1); //右相邻 }
但是还会存在着边界情况,
对于网格边缘的方格,上下左右并不都有邻居。一种做法是在递归调用之前判断方格的位置,例如位于左边缘,则不访问其左邻居。但这样一个一个判断写起来比较麻烦,我们可以用“先污染后治理”的方法,先做递归调用,再在每个 DFS 函数的开头判断坐标是否合法,不合法的直接返回。同样地,我们还需要判断该方格是否有岛屿(值是否为 1),否则也需要返回。
void Create_DFS(int[][] grid, int r, int c) {//row and column //非法情况:不在网格内部---->直接返回 if (!(r >= 0 && r < grid.length && c >= 0 && c < grid[0].length)) { return; } //不是岛屿情况---->直接返回 if (grid[r][c] != 1) { return; } //如果是岛屿,走过之后要记得留痕迹,否则会一直打转转 grid[r][c] = 2; DFS_G(grid, r - 1, c);//上相邻 DFS_G(grid, r + 1, c);//下相邻 DFS_G(grid, r, c - 1);//左相邻 DFS_G(grid, r, c + 1);//右相邻 }
到此为止,基于网格的DFS问题模板已经完成。
————————————————————————————————————————————————————————————————————————————————————————————
接下来是具体问题具体分析:
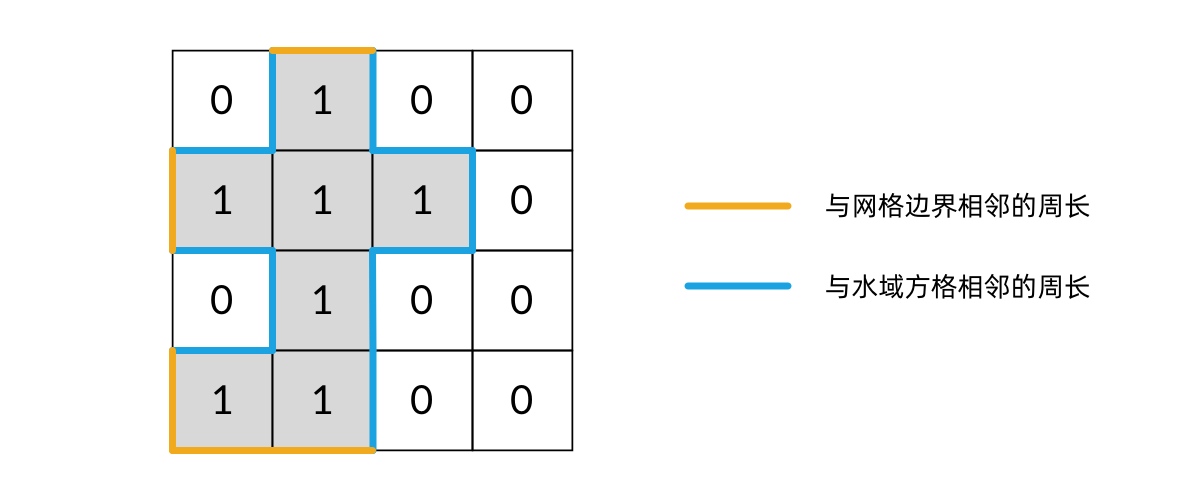
观察问题给出的示例图,发现:
1. 岛屿---->边界,周长+1
2.岛屿---->水域,周长+1
3.岛屿---->岛屿,周长不变化
此时,基于模板进行修改即可。
int Create_DFS_grith(int[][] grid, int r, int c) {//row and column //非法情况:不在网格内部 //岛屿---->边界,周长+1 if (!(r >= 0 && r < grid.length && c >= 0 && c < grid[0].length)) { return 1; } //岛屿---->水域,周长+1 if(grid[r][c]==0){ return 1; } //岛屿---->岛屿,周长不变化 if (grid[r][c] != 1) { return 0; } //如果是岛屿,走过之后要记得留痕迹,否则会一直打转转 grid[r][c] = 2; return DFS_G(grid, r - 1, c)+ DFS_G(grid, r + 1, c)+ DFS_G(grid, r, c - 1)+ DFS_G(grid, r, c + 1); }
public int islandPerimeter(int[][] grid) { for (int r = 0; i < grid.length; r++) { for (int c = 0; j < grid[0].length; c++) {
// 题目限制只有一个岛屿,计算一个即可 if (grid[r][c] == 1) return Create_DFS_grith(grid, r, c); } } return 0; }
给你一个由 ‘1‘(陆地)和 ‘0‘(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1
示例 2:
输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:3
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 ‘0‘ 或 ‘1‘
________________________________________________________________________________________________________________________________________________________________________
依旧是,具体问题具体分析,基于模板适当修改
//“感染”函数,将所有连接在一起的岛屿“感染”
public void DFS(char[][] grid, int r, int c) { //非法情况 and 走过 if (r < 0 || r >= grid.length || c < 0 || c >= grid[0].length || grid[r][c] != ‘1‘) { return; } grid[r][c] = ‘2‘;//走过的岛屿留记号 DFS(grid, r + 1, c); DFS(grid, r - 1, c); DFS(grid, r, c + 1); DFS(grid, r, c - 1); }
public int numIslands(char[][] grid) { int cnt_island = 0; //记录岛屿数量 for (int i = 0; i < grid.length; i++) { for (int j = 0; j < grid[0].length; j++) { if (grid[i][j] == ‘1‘) { DFS(grid, i, j); cnt_island++; } } } return cnt_island; }
解题思路,参考大神思路 作者:nettee 链接:https://leetcode-cn.com/problems/island-perimeter/solution/tu-jie-jian-ji-er-qiao-miao-de-dfs-fang-fa-java-by/ 来源:力扣(LeetCode) 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
标签:http rgba src loading 观察 假设 没有 data color
原文地址:https://www.cnblogs.com/ANullValue/p/13907252.html