码迷，mamicode.com
首页 > 其他好文 > 详细

[kuangbin带你飞]专题七 线段树

时间：2020-11-01 21:18:27      阅读：19      评论：0      收藏：0      [点我收藏+]

标签：初始   延迟标记   最大连续   之间   tin   端点   add   geo   algo   

1. HDU1166 敌兵布阵

题目链接

题意：单点更新+区间查询(求和)。

树状数组 (218ms)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, N = 5e4 + 5;

int t, n;
int c[N];
char str[10];

int lowbit(int x) { return x & -x; }

void add(int x, int v) {
    for (; x <= n; x += lowbit(x)) c[x] += v;
}

int sum(int x) {
    int res = 0;
    for (; x; x -= lowbit(x)) res += c[x];
    return res;
}

int main() 
{
    scanf("%d", &t);
    for (int cas = 1; cas <= t; ++cas) {
        scanf("%d", &n);
        int x, y;
        memset(c, 0, sizeof(c));
        for (int i = 1; i <= n; ++i) {
            scanf("%d", &x);
            add(i, x);
        }
        printf("Case %d:\n", cas);
        while (scanf("%s", str) && str[0] != ‘E‘) {
            scanf("%d%d", &x, &y);
            if (str[0] == ‘A‘) add(x, y);
            else if (str[0] == ‘S‘) add(x, -y);
            else printf("%d\n", sum(y) - sum(x - 1));
        }
    }
    return 0;
}

线段树 (234ms)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, N = 5e4 + 5;

struct Node {
    int l, r, sum;
}tree[N<<2];

int t, n;
int a[N];
char str[10];

void push_up(int rt) {
    tree[rt].sum = tree[rt<<1].sum + tree[rt<<1|1].sum;
}

void build(int rt, int l, int r) {
    tree[rt].l = l, tree[rt].r = r;
    if (l == r) { tree[rt].sum = a[l]; return; }
    int mid = (l + r) >> 1;
    build(rt<<1, l, mid);
    build(rt<<1|1, mid + 1, r);
    push_up(rt);
}

void update(int rt, int x, int v) {
    if (tree[rt].l == tree[rt].r) { tree[rt].sum += v; return; }
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if (x <= mid) update(rt<<1, x, v);
    else update(rt<<1|1, x, v);
    push_up(rt);
}

int query(int rt, int l, int r) {
    if (l <= tree[rt].l && r >= tree[rt].r) return tree[rt].sum;
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    int ans = 0;
    if (l <= mid) ans += query(rt<<1, l, r);
    if (r > mid) ans += query(rt<<1|1, l, r);
    return ans;
}

int main()
{
    scanf("%d", &t);
    for (int cas = 1; cas <= t; ++cas) {
        scanf("%d", &n);
        for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
        build(1, 1, n);
        int x, y;
        printf("Case %d:\n", cas);
        while (scanf("%s", str) && str[0] != ‘E‘) {
            scanf("%d%d", &x, &y);
            if (str[0] == ‘A‘) update(1, x, y);
            else if (str[0] == ‘S‘) update(1, x, -y);
            else printf("%d\n", query(1, x, y));
        }
    }
    return 0;
}

zkw(张昆玮) 线段树 (202ms)

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, N = 5e4 + 5;

int t, n, m;
int tree[N<<2];
char str[10];

void push_up(int rt) {
    tree[rt] = tree[rt<<1] + tree[rt<<1|1];
} 

void build() {
    for (m = 1; m <= n + 1; m <<= 1);
    for (int i = m + 1; i <= m + n; ++i) scanf("%d", &tree[i]);
    for (int i = m - 1; i; --i) push_up(i);
}

void update(int x, int v) {
    for (x += m; x; x >>= 1) tree[x] += v;
}

int query(int l, int r) {
    int res = 0;
    for (l = l + m - 1, r = r + m + 1; l ^ r ^ 1; l >>= 1, r >>= 1) {
        if (~l & 1) res += tree[l ^ 1];
        if (r & 1) res += tree[r ^ 1];
    }
    return res;
}

int main() 
{
    scanf("%d", &t);
    for (int cas = 1; cas <= t; ++cas) {
        scanf("%d", &n);
        build();
        int x, y;
        printf("Case %d:\n", cas);
        while (scanf("%s", str) && str[0] != ‘E‘) {
            scanf("%d%d", &x, &y);
            if (str[0] == ‘A‘) update(x, y);
            else if (str[0] == ‘S‘) update(x, -y);
            else printf("%d\n", query(x, y));
        }
    }
    return 0;
}

2. HDU1754 I Hate It

题目链接

题意：单点更新+区间查询(最值)。

??模板题。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, N = 2e5 + 5;

struct Node {
    int l, r, dat;
}tree[N<<2];

int n, m;
int a[N];
char op[3];

void push_up(int rt) {
    tree[rt].dat = max(tree[rt<<1].dat, tree[rt<<1|1].dat);
}

void build(int rt, int l, int r) {
    tree[rt].l = l, tree[rt].r = r;
    if (l == r) { tree[rt].dat = a[l]; return; }
    int mid = (l + r) >> 1;
    build(rt<<1, l, mid);
    build(rt<<1|1, mid + 1, r);
    push_up(rt);
}

void update(int rt, int x, int v) {
    if (tree[rt].l == tree[rt].r) { tree[rt].dat = v; return; }
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if (x <= mid) update(rt<<1, x, v);
    else update(rt<<1|1, x, v);
    push_up(rt);
}

int query(int rt, int l, int r) {
    if (l <= tree[rt].l && r >= tree[rt].r) return tree[rt].dat;
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    int res = 0;
    if (l <= mid) res = max(res, query(rt<<1, l, r));
    if (r > mid) res = max(res, query(rt<<1|1, l, r));
    return res;
}

int main() 
{
    while (~scanf("%d%d", &n, &m)) {
        for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
        build(1, 1, n);
        int x, y;
        while (m--) {
            scanf("%s%d%d", op, &x, &y);
            if (op[0] == ‘Q‘) printf("%d\n", query(1, x, y));
            else if (op[0] == ‘U‘) update(1, x, y);
        }
    }
    return 0;
}

3. POJ3468 A Simple Problem with Integers

题目链接

题意：区间更新+区间查询(求和)。

??模板题，延迟标记。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, N = 1e5 + 5;

struct Node {
    int l, r;
    ll sum, add;
}tree[N<<2];

int n, q;
int a[N];
char op[3];

void push_down(int rt) {
    if (tree[rt].add) {
        tree[rt<<1].sum += tree[rt].add * (tree[rt<<1].r - tree[rt<<1].l + 1);
        tree[rt<<1|1].sum += tree[rt].add * (tree[rt<<1|1].r - tree[rt<<1|1].l + 1);
        tree[rt<<1].add += tree[rt].add;
        tree[rt<<1|1].add += tree[rt].add;
        tree[rt].add = 0;
    }
}

void push_up(int rt) {
    tree[rt].sum = tree[rt<<1].sum + tree[rt<<1|1].sum;
}

void build(int rt, int l, int r) {
    tree[rt].l = l, tree[rt].r = r;
    if (l == r) { tree[rt].sum = a[l]; return; }
    int mid = (l + r) >> 1;
    build(rt<<1, l, mid);
    build(rt<<1|1, mid + 1, r);
    push_up(rt);
}

void update(int rt, int l, int r, int d) {
    if (l <= tree[rt].l && r >= tree[rt].r) {
        tree[rt].sum += (ll)d * (tree[rt].r - tree[rt].l + 1);
        tree[rt].add += d;
        return;
    }
    push_down(rt);
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if (l <= mid) update(rt<<1, l, r, d);
    if (r > mid) update(rt<<1|1, l, r, d);
    push_up(rt);
}

ll query(int rt, int l, int r) {
    if (l <= tree[rt].l && r >= tree[rt].r) return tree[rt].sum;
    push_down(rt);
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    ll res = 0;
    if (l <= mid) res += query(rt<<1, l, r);
    if (r > mid) res += query(rt<<1|1, l, r);
    return res;
}

int main() 
{
    scanf("%d%d", &n, &q);
    for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
    build(1, 1, n);
    while (q--) {
        int x, y, z;
        scanf("%s%d%d", op, &x, &y);
        if (op[0] == ‘C‘) {
            scanf("%d", &z);
            update(1, x, y, z);
        }
        else if (op[0] == ‘Q‘) printf("%lld\n", query(1, x, y));
    }
    return 0;
}

4. POJ2528 Mayor‘s posters

题目链接

题意：市长选举贴高度相同的海报，后面的海报可以贴在前面的上面，最后可以看见的海报。

??离散化用线段树，注意对于如 \([1,10],[1,4],[6,10]\) 等端点重合的样例，离散化将 5 压缩掉，因此需要在距离大于 1 的点中进行插点，不影响最终结果，在 \(2 * N\) 个点中插点，最多 \(4 * N-1\)，因此取 \(N=4e4\)。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, N = 4e4 + 5;

struct Node {
    int l, r, lazytag;
}tree[N<<2];

int cas, n, ans;
int pl[N], pr[N], seg[N<<1];
int vis[N<<1];

void push_down(int rt) {
    if (tree[rt].lazytag) {
        tree[rt<<1].lazytag = tree[rt<<1|1].lazytag = tree[rt].lazytag;
        tree[rt].lazytag = 0;
    }
}

void build(int rt, int l, int r) {
    tree[rt].l = l, tree[rt].r = r;
    tree[rt].lazytag = 0;
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(rt<<1, l, mid);
    build(rt<<1|1, mid + 1, r);
}

void update(int rt, int l, int r, int x) {
    if (l <= tree[rt].l && r >= tree[rt].r) {
        tree[rt].lazytag = x;
        return;
    }
    push_down(rt);
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if (l <= mid) update(rt<<1, l, r, x);
    if (r > mid) update(rt<<1|1, l, r, x);
}

void query(int rt) {
    if (tree[rt].lazytag && !vis[tree[rt].lazytag]) {
        ans++;
        vis[tree[rt].lazytag] = 1;
        return;
    }
    if (tree[rt].l == tree[rt].r) return;
    push_down(rt);
    query(rt<<1);
    query(rt<<1|1);
}

int main() 
{
    scanf("%d", &cas);
    while (cas--) {
        int cnt = 0;
        memset(vis, 0, sizeof(vis));
        scanf("%d", &n);
        for (int i = 1; i <= n; ++i) {
            scanf("%d%d", &pl[i], &pr[i]);
            seg[++cnt] = pl[i];
            seg[++cnt] = pr[i];
        }
        sort(seg + 1, seg + cnt + 1);
        int m = unique(seg + 1, seg + cnt + 1) - (seg + 1);
        for (int i = m; i >= 2; --i)
            if (seg[i] - seg[i-1] > 1) seg[++m] = seg[i-1] + 1;
        sort(seg + 1, seg + m + 1);
        build(1, 1, m);
        for (int i = 1; i <= n; ++i) {
            int x = lower_bound(seg + 1, seg + m + 1, pl[i]) - seg;
            int y = lower_bound(seg + 1, seg + m + 1, pr[i]) - seg;
            update(1, x, y, i);
        }
        ans = 0;
        query(1);
        printf("%d\n", ans);
    }
    return 0;
}

5. HDU1698 Just a Hook

题目链接

题意：区间更新+所有数的和。

??延迟标记，最后输出 tree[1].sum 即可。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, N = 1e5 + 5;

struct Node {
    int l, r, sum, tag;
}tree[N<<2];

int cas, n, q;

void push_up(int rt) {
    tree[rt].sum = tree[rt<<1].sum + tree[rt<<1|1].sum;
}

void push_down(int rt) {
    if (tree[rt].tag) {
        tree[rt<<1].tag = tree[rt<<1|1].tag = tree[rt].tag;
        int mid = (tree[rt].l + tree[rt].r) >> 1;
        tree[rt<<1].sum = (mid - tree[rt].l + 1) * tree[rt].tag;
        tree[rt<<1|1].sum = (tree[rt].r - mid) * tree[rt].tag;
        tree[rt].tag = 0;
    }
}

void build(int rt, int l, int r) {
    tree[rt].l = l, tree[rt].r = r;
    tree[rt].tag = 0;
    if (l == r) { tree[rt].sum = 1; return; }
    int mid = (l + r) >> 1;
    build(rt<<1, l, mid);
    build(rt<<1|1, mid + 1, r);
    push_up(rt);
}

void update(int rt, int l, int r, int x) {
    if (l <= tree[rt].l && r >= tree[rt].r) {
        tree[rt].sum = x * (tree[rt].r - tree[rt].l + 1);
        tree[rt].tag = x;
        return;
    }
    push_down(rt);
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if (l <= mid) update(rt<<1, l, r, x);
    if (r > mid) update(rt<<1|1, l, r, x);
    push_up(rt);
}

int main() 
{
    scanf("%d", &cas);
    for (int i = 1; i <= cas; ++i) {
        scanf("%d%d", &n, &q);
        build(1, 1, n);
        int x, y, z;
        while (q--) {
            scanf("%d%d%d", &x, &y, &z);
            update(1, x, y, z);
        }
        printf("Case %d: The total value of the hook is %d.\n", i, tree[1].sum);
    }
    return 0;
}

6. ZOJ1610 Count the Colors

题目链接

题意：区间涂色（可覆盖），求最终可看到几种颜色，以及这些颜色的段数。

??类似于第四题，延迟标记。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, N = 8e3 + 5;

struct Node {
    int l, r, tag;
}tree[N<<2];

int n, last;
int vis[N];

void push_down(int rt) {
    if (~tree[rt].tag) {
        tree[rt<<1].tag = tree[rt<<1|1].tag = tree[rt].tag;
        tree[rt].tag = -1;
    }
}

void build(int rt, int l, int r) {
    tree[rt].l = l, tree[rt].r = r;
    tree[rt].tag = -1;
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(rt<<1, l, mid);
    build(rt<<1|1, mid + 1, r); 
}

void update(int rt, int l, int r, int x) {
    if (l <= tree[rt].l && r >= tree[rt].r) {
        tree[rt].tag = x;
        return;
    }
    push_down(rt);
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if (l <= mid) update(rt<<1, l, r, x);
    if (r > mid) update(rt<<1|1, l, r, x);
}

void query(int rt) {
    if (tree[rt].l == tree[rt].r)  {
        if (~tree[rt].tag && tree[rt].tag != last) {
            vis[tree[rt].tag]++;
        }
        last = tree[rt].tag;
        return;
    }
    push_down(rt);
    query(rt<<1);
    query(rt<<1|1);
}

int main() 
{
    while (~scanf("%d", &n)) {
        memset(vis, 0, sizeof(vis));
        build(1, 1, 8000);
        int x, y, z;
        while (n--) {
            scanf("%d%d%d", &x, &y, &z);
            update(1, x + 1, y, z);
        }
        last = -1;
        query(1);
        for (int i = 0; i <= 8000; ++i) {
            if (vis[i]) printf("%d %d\n", i, vis[i]);
        }
        puts("");
    }
    return 0;
}

7. POJ3264 Balanced Lineup

题目链接

题意：农夫 Jorn 的 n 中奶牛排成一列，q 个查询，输出区间最大高度差。

树状数组

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, N = 5e4 + 5;

int n, q;
int a[N], minn[N], maxn[N];

int lowbit(int x) { return x & -x; }

void update(int x, int v) {
    for (; x <= n; x += lowbit(x)) {
        maxn[x] = max(maxn[x], v);
        minn[x] = min(minn[x], v);
    }
}

int ask(int l, int r) {
    int ma = a[l], mi = a[l];
    while (r >= l) {
        ma = max(ma, a[r]); mi = min(mi, a[r]);
        for (r--; r - lowbit(r) >= l; r -= lowbit(r))
            ma = max(ma, maxn[r]), mi = min(mi, minn[r]);
    }
    return ma - mi;
}

int main() 
{
    scanf("%d%d", &n, &q);
    memset(minn, 0x3f, sizeof(minn));
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &a[i]);
        update(i, a[i]);
    }
    int x, y;
    while (q--) {
        scanf("%d%d", &x, &y);
        printf("%d\n", ask(x, y));
    }
    return 0;
}

线段树

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, N = 5e4 + 5;

struct Node {
    int l, r, high, low;
}tree[N<<2];

int n, q;
int a[N];

void push_up(int rt) {
    tree[rt].high = max(tree[rt<<1].high, tree[rt<<1|1].high);
    tree[rt].low = min(tree[rt<<1].low, tree[rt<<1|1].low);
}

void build(int rt, int l, int r) {
    tree[rt].l = l, tree[rt].r = r;
    if (l == r) {
        tree[rt].high = tree[rt].low = a[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(rt<<1, l, mid);
    build(rt<<1|1, mid + 1, r);
    push_up(rt);
}

int query(int rt, int l, int r, int f) {
    if (l <= tree[rt].l && r >= tree[rt].r) {
        if (f) return tree[rt].high;
        else return tree[rt].low;
    }
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    int res; if (f) res = 0; else res = INF;
    if (l <= mid) {
        if (f) res = max(res, query(rt<<1, l, r, 1));
        else res = min(res, query(rt<<1, l, r, 0));
    }
    if (r > mid) {
        if (f) res = max(res, query(rt<<1|1, l, r, 1));
        else res = min(res, query(rt<<1|1, l, r, 0));
    }
    return res;
}

int main() 
{
    scanf("%d%d", &n, &q);
    for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
    build(1, 1, n);
    int x, y;
    while (q--) {
        scanf("%d%d", &x, &y);
        printf("%d\n", query(1, x, y, 1) - query(1, x, y, 0));
    }
    return 0;
}

8. HDU4027 Can you answer these queries?

题目链接

题意：区间修改(开方)+区间查询(求和)。

??每个点更新不一样，只能单点修改，由于 \(2^{64}\) 开 7 次方取整为 1，故还可加限制条件每个点最多更新 7 次，以及区间和等于区间长度时不需继续更新，注意输入数组不开 long long 会 TLE。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, N = 1e5 + 5;

struct Node {
    int l, r;
    ll sum;
}tree[N<<2];

int n, m, cas;
ll a[N];

void push_up(int rt) {
    tree[rt].sum = tree[rt<<1].sum + tree[rt<<1|1].sum;
}

void build(int rt, int l, int r) {
    tree[rt].l = l, tree[rt].r = r;
    if (l == r) { tree[rt].sum = a[l]; return; }
    int mid = (l + r) >> 1;
    build(rt<<1, l, mid);
    build(rt<<1|1, mid + 1, r);
    push_up(rt);
}

void update(int rt, int l, int r) {
    if (tree[rt].sum == ll(tree[rt].r - tree[rt].l + 1)) return;
    if (tree[rt].l == tree[rt].r) {
        tree[rt].sum = (ll)sqrt(tree[rt].sum);
        return;
    }
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if (l <= mid) update(rt<<1, l, r);
    if (r > mid) update(rt<<1|1, l, r);
    push_up(rt);
}

ll query(int rt, int l, int r) {
    if (l <= tree[rt].l && r >= tree[rt].r) return tree[rt].sum;
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    ll res = 0;
    if (l <= mid) res += query(rt<<1, l, r);
    if (r > mid) res += query(rt<<1|1, l, r);
    return res;
}

int main() 
{
    while (~scanf("%d", &n)) {
        for (int i = 1; i <= n; ++i) scanf("%lld", &a[i]);
        build(1, 1, n);
        scanf("%d", &m);
        printf("Case #%d:\n", ++cas);
        int t, x, y;
        while (m--) {
            scanf("%d%d%d", &t, &x, &y);
            if (x > y) swap(x, y);
            if (t) printf("%lld\n", query(1, x, y));
            else update(1, x, y);
            
        }
        puts("");
    }
    return 0;
}

9. HDU1540 Tunnel Warfare

题目链接

题意：n 个地道，m 个操作，D x: 炸掉第 x 个地道；Q x: 查询第 x 个地道所在的最大区间长度；R x: 重建上一次被炸的地道。

??法一：线段树维护三个信息，ll: 左端点开始最大连续长度，rl: 右端点开始最大连续长度，ml: 区间中最大连续长度。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, N = 5e4 + 5;

struct Node {
    int l, r;
    int ll, rl, ml;
}tree[N<<2];

int n, m;
int sta[N];
char op[3];

void push_up(int rt) {
    tree[rt].ll = tree[rt<<1].ll, tree[rt].rl = tree[rt<<1|1].rl;
    tree[rt].ml = max(tree[rt<<1].ml, tree[rt<<1|1].ml);
    tree[rt].ml = max(tree[rt].ml, tree[rt<<1].rl + tree[rt<<1|1].ll);
    if (tree[rt].ll == tree[rt<<1].r - tree[rt<<1].l + 1) tree[rt].ll += tree[rt<<1|1].ll;
    if (tree[rt].rl == tree[rt<<1|1].r - tree[rt<<1|1].l + 1) tree[rt].rl += tree[rt<<1].rl;
}

void build(int rt, int l, int r) {
    tree[rt].l = l, tree[rt].r = r;
    tree[rt].ll = tree[rt].rl = tree[rt].ml = r - l + 1;
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(rt<<1, l, mid);
    build(rt<<1|1, mid + 1, r);
}

void update(int rt, int x, int v) {
    if (tree[rt].l == tree[rt].r) {
        tree[rt].ll = tree[rt].rl = tree[rt].ml = v;
        return;
    }
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if (x <= mid) update(rt<<1, x, v);
    else update(rt<<1|1, x, v);
    push_up(rt);
}

int query(int rt, int x) {
    if (tree[rt].l == tree[rt].r || !tree[rt].ml || tree[rt].ml == tree[rt].r - tree[rt].l + 1) return tree[rt].ml;
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if (x <= mid) {
        if (x >= mid - tree[rt<<1].rl + 1)
            return tree[rt<<1].rl + tree[rt<<1|1].ll;
        else return query(rt<<1, x);
    }
    else {
        if (x <= mid + tree[rt<<1|1].ll)
            return tree[rt<<1|1].ll + tree[rt<<1].rl;
        else return query(rt<<1|1, x);
    }
}

int main() 
{
    while (~scanf("%d%d", &n, &m)) {
        build(1, 1, n);
        int top = 0, x;
        while (m--) {
            scanf("%s", op);
            if (op[0] == ‘D‘) {
                scanf("%d", &x);
                sta[++top] = x;
                update(1, x, 0);
            }
            else if (op[0] == ‘Q‘) {
                scanf("%d", &x);
                printf("%d\n", query(1, x));
            }
            else if (op[0] == ‘R‘) {
                if (!top) continue;
                x = sta[top--];
                update(1, x, 1);
            }
        }
    }
    return 0;
}

??法二：线段树维护区间中被摧毁村庄编号的最值。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, N = 5e4 + 5;

struct Node {
    int l, r;
    int mi, ma;
}tree[N<<2];

int n, m;
int sta[N];
char op[3];

void push_up(int rt) {
    tree[rt].mi = min(tree[rt<<1].mi, tree[rt<<1|1].mi);
    tree[rt].ma = max(tree[rt<<1].ma, tree[rt<<1|1].ma);
}

void build(int rt, int l, int r) {
    tree[rt].l = l, tree[rt].r = r;
    tree[rt].mi = n + 1, tree[rt].ma = 0;
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(rt<<1, l, mid);
    build(rt<<1|1, mid + 1, r);
}

void update(int rt, int x, int v) {
    if (tree[rt].l == tree[rt].r) {
        if (v) { tree[rt].mi = n + 1; tree[rt].ma = 0; }
        else tree[rt].mi = tree[rt].ma = x;
        return;
    }
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if (x <= mid) update(rt<<1, x, v);
    else update(rt<<1|1, x, v);
    push_up(rt);
}

int query(int rt, int x, int f) {
    int mid = (tree[rt].l + tree[rt].r) >> 1, res;
    if (f) {
        if (tree[rt].r <= x || tree[rt].l == tree[rt].r) {
            return tree[rt].ma;
        }
        res = 0;
        res = max(res, query(rt<<1, x, 1));
        if (mid < x) res = max(res, query(rt<<1|1, x, 1));
        return res;
    }
    else {
        if (tree[rt].l >= x || tree[rt].l == tree[rt].r) {
            return tree[rt].mi;
        }
        res = n + 1;
        res = min(res, query(rt<<1|1, x, 0));
        if (x <= mid) res = min(res, query(rt<<1, x, 0));
        return res;
    }
}

int main() 
{
    while (~scanf("%d%d", &n, &m)) {
        build(1, 1, n);
        int top = 0, x;
        while (m--) {
            scanf("%s", op);
            if (op[0] == ‘D‘) {
                scanf("%d", &x);
                sta[++top] = x;
                update(1, x, 0);
            }
            else if (op[0] == ‘Q‘) {
                scanf("%d", &x);
                int r = query(1, x, 0);
                int l = query(1, x, 1);
                if (l == r) puts("0");
                else printf("%d\n", r - l - 1);
            }
            else if (op[0] == ‘R‘) {
                if (!top) continue;
                x = sta[top--];
                update(1, x, 1);
            }
        }
    }
    return 0;
}

??法三：类似法二的思想，模拟来做。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <set>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, N = 5e4 + 5;

int n, m;
int sta[N];
char op[3];
set<int> s;

int main() 
{
    while (~scanf("%d%d", &n, &m)) {
        s.clear();
        int top = 0, x;
        while (m--) {
            scanf("%s", op);
            if (op[0] == ‘D‘) {
                scanf("%d", &x);
                sta[++top] = x;
                s.insert(x);
            }
            else if (op[0] == ‘Q‘) {
                scanf("%d", &x);
                set<int>::iterator it = s.lower_bound(x);
                int l, r;
                if (it == s.end()) r = n + 1;
                else r = *it;
                if (it == s.begin()) l = 0;
                else l = *(--it);
                if (r == x) puts("0");
                else printf("%d\n", r - l - 1);
            }
            else if (op[0] == ‘R‘) {
                s.erase(sta[top--]);
            }
        }
    }
    return 0;
}

10. HDU3974 Assign the task

题目链接

题意：n 个结点，n-1 个关系，所有结点初始值为 -1，给出 m 个操作，C x: 查询 x 结点的值，T x y: 以 x 为根的子树上所有结点值变成 y。

??dfs 找出树的 dfs 序，找出每个数字左右两边出现的位置，子结点必在两个位置之间，之后用线段树即可。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, N = 5e4 + 5;

struct Node {
    int l, r, dat, lazy;
}tree[N<<2];

int t, n, m, tot, root;
int head[N], L[N], R[N];
int ver[N], nxt[N];
char op[3];

void add(int x, int y) {
    ver[++tot] = y;
    nxt[tot] = head[x];
    head[x] = tot;
}

void dfs(int x) {
    L[x] = ++tot;
    for (int i = head[x]; i; i = nxt[i]) {
        dfs(ver[i]);
    }
    R[x] = ++tot;	
}

void push_down(int rt) {
    if (tree[rt].lazy) {
        tree[rt<<1].dat = tree[rt<<1|1].dat = tree[rt].lazy;
        tree[rt<<1].lazy = tree[rt<<1|1].lazy = tree[rt].lazy;
        tree[rt].lazy = 0;
    }
}

void build(int rt, int l, int r) {
    tree[rt].l = l, tree[rt].r = r, tree[rt].lazy = 0;
    if (l == r) { tree[rt].dat = -1; return; }
    int mid = (l + r) >> 1;
    build(rt<<1, l, mid);
    build(rt<<1|1, mid + 1, r);
}

void update(int rt, int l, int r, int v) {
    if (l <= tree[rt].l && r >= tree[rt].r) {
        tree[rt].dat = v;
        tree[rt].lazy = v;
        return;
    }
    push_down(rt);
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if (l <= mid) update(rt<<1, l, r, v);
    if (r > mid) update(rt<<1|1, l, r, v);
}

int query(int rt, int x) {
    if (tree[rt].l == tree[rt].r) {
        return tree[rt].dat;
    }
    push_down(rt);
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if (x <= mid) return query(rt<<1, x);
    else return query(rt<<1|1, x);
}

int main() 
{
    scanf("%d", &t);
    for (int cas = 1; cas <= t; ++cas) {
        scanf("%d", &n);
        tot = 0, root = n * (n + 1) / 2;
        for (int i = 1; i <= n; ++i) {
            head[i] = 0;
        }
        int x, y;
        for (int i = 1; i < n; ++i) {
            scanf("%d%d", &x, &y);
            root -= x;
            add(y, x);
        }
        tot = 0;
        dfs(root);
        build(1, 1, n<<1);
        scanf("%d", &m);
        printf("Case #%d:\n", cas);
        while (m--) {
            scanf("%s%d", op, &x);
            if (op[0] == ‘C‘) {
                printf("%d\n", query(1, L[x]));
            }
            else if (op[0] == ‘T‘) {
                scanf("%d", &y);
                update(1, L[x], R[x], y);
            }
        }

    }
    return 0;
}

11. HDU4578 Transformation

题目链接

题意：给定一个长度为 n 的序列，有 4 种操作:

  1. 1 x y c [x, y] 上的值全部加 c
  2. 2 x y c [x, y] 上的值全部乘 c
  3. 3 x y c [x, y] 上的值全部赋为 c
  4. 4 x y p [x, y] 上的值的 p 次方和

??线段树维护延迟标记 加(add), 乘(mul)，以及 sum[i] 表示 i 次方的和，更新时考虑 add、mul 对 sum[i] 的影响

乘法：

  • \(sum[i] = v ^ i * sum[i]\)

加法

  • \(sum[3] = sum[3] + 3v^2 * sum[1] + 3v * sum[2] + len * v^3\)
  • \(sum[2] = sum[2] + 2v * sum[2] + len * v^2\)
  • \(sum[1] = sum[1] + len * v\)

其中 len 为当前区间的长度。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, MOD = 1e4 + 7, N = 1e5 + 5;

struct Node {
    int l, r, add, mul;
    int sum[4];
    void _mul(int v) {
        mul = (mul * v) % MOD;
        add = (add * v) % MOD;
        for (int i = 1; i <= 3; ++i) {
            for (int p = 1; p <= i; ++p) {
                sum[i] = (sum[i] * v) % MOD;
            }
        }
    }
    void _add(int v) {
        add = (add + v) % MOD;
        int len = r - l + 1;
        sum[3] = (sum[3] + 3 * v % MOD * v % MOD * sum[1] % MOD) % MOD;
        sum[3] = (sum[3] + 3 * v % MOD * sum[2] % MOD) % MOD;
        sum[3] = (sum[3] + len * v % MOD * v % MOD * v % MOD) % MOD;
        sum[2] = (sum[2] + 2 * v % MOD * sum[1] % MOD) % MOD;
        sum[2] = (sum[2] + len * v % MOD * v % MOD) % MOD;
        sum[1] = (sum[1] + len * v % MOD) % MOD;
    }
    void calc(int MUL, int ADD) {
        _mul(MUL);
        _add(ADD);
    }
}tree[N<<2];

int n, m;

void push_up(int rt) {
    for (int i = 1; i <= 3; ++i) {
        tree[rt].sum[i] = (tree[rt<<1].sum[i] + tree[rt<<1|1].sum[i]) % MOD;
    }
}

void push_down(int rt) {
    if (tree[rt].add || tree[rt].mul != 1) {
        tree[rt<<1].calc(tree[rt].mul, tree[rt].add);
        tree[rt<<1|1].calc(tree[rt].mul, tree[rt].add);
        tree[rt].add = 0, tree[rt].mul = 1;
    }
}

void build(int rt, int l, int r) {
    tree[rt].l = l, tree[rt].r = r;
    tree[rt].add = 0, tree[rt].mul = 1;
    for (int i = 1; i <= 3; ++i) tree[rt].sum[i] = 0;
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(rt<<1, l, mid);
    build(rt<<1|1, mid + 1, r);
}

void update(int rt, int l, int r, int v, int op) {
    if (l <= tree[rt].l && r >= tree[rt].r) {
        if (op == 1) tree[rt].calc(1, v);
        else if (op == 2) tree[rt].calc(v, 0);
        else if (op == 3) tree[rt].calc(0, v);
        return;
    }
    push_down(rt);
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if (l <= mid) update(rt<<1, l, r, v, op);
    if (r > mid) update(rt<<1|1, l, r, v, op);
    push_up(rt);
}

int query(int rt, int l, int r, int p) {
    if (l <= tree[rt].l && r >= tree[rt].r) return tree[rt].sum[p];
    push_down(rt);
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    int res = 0;
    if (l <= mid) res = (res + query(rt<<1, l, r, p)) % MOD;
    if (r > mid) res = (res + query(rt<<1|1, l, r, p)) % MOD;
    return res;
}

int main() 
{
    while (scanf("%d%d", &n, &m), n || m) {
        build(1, 1, n);
        int op, x, y, z;
        while (m--) {
            scanf("%d%d%d%d", &op, &x, &y, &z);
            if (op == 4) {
                printf("%d\n", query(1, x, y, z) % MOD);
            }
            else update(1, x, y, z, op);
        }
    }
    return 0;
}

12. HDU4614 Vases and Flowers

题目链接

题意：有 n 个空花瓶 \(0\sim n-1\)，m 个操作：1 x y: 从 x 位置插 y 多花，有花的花瓶跳过，到最后一个花瓶还有剩余，丢弃剩余花；2 x y: 将区间 \([x,y]\)的花瓶清空。对 1 操作，输出第一个和最后一个插花的位置，如果一朵花都插不了，输出 ‘Can not put any one.‘；对 2 操作，输出区间 \([x,y]\) 内被清空的花瓶数量。

??线段树维护区间空花瓶数 num 和一个延迟标记 tag，对操作 1，判断所求区间空花瓶数大于 0，区间空花瓶递增，可二分找到第一个和最后一个插花位置，将两个位置间 num 置 0；对操作 2，输出总数减空花瓶数，之后区间 num 置为区间长度。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, N = 5e4 + 5;

struct Node {
    int l, r;
    int num, tag;
}tree[N<<2];

int t, n, m;

void push_up(int rt) {
    tree[rt].num = tree[rt<<1].num + tree[rt<<1|1].num;
}

void push_down(int rt) {
    if (~tree[rt].tag) {
        tree[rt<<1].tag = tree[rt<<1|1].tag = tree[rt].tag;
        int mid = (tree[rt].l + tree[rt].r) >> 1;
        tree[rt<<1].num = (mid - tree[rt].l + 1) * tree[rt].tag;
        tree[rt<<1|1].num = (tree[rt].r - mid) * tree[rt].tag;
        tree[rt].tag = -1;
    }
}

void build(int rt, int l, int r) {
    tree[rt].l = l, tree[rt].r = r;
    tree[rt].num = r - l + 1, tree[rt].tag = -1;
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(rt<<1, l, mid);
    build(rt<<1|1, mid + 1, r);
}

void update(int rt, int l, int r, int f) {
    if (l <= tree[rt].l && r >= tree[rt].r) {
        tree[rt].num = (tree[rt].r - tree[rt].l + 1) * f;
        tree[rt].tag = f;
        return;
    }
    push_down(rt);
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if (l <= mid) update(rt<<1, l, r, f);
    if (r > mid) update(rt<<1|1, l, r, f);
    push_up(rt);
}

int query(int rt, int l, int r) {
    if (l <= tree[rt].l && r >= tree[rt].r) return tree[rt].num;
    push_down(rt);
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    int res = 0;
    if (l <= mid) res += query(rt<<1, l, r);
    if (r > mid) res += query(rt<<1|1, l, r);
    return res;
}

int search(int x, int num) {
    int l = x, r = n;
    while (l < r) {
        int mid = (l + r) >> 1;
        if (query(1, x, mid) >= num) r = mid;
        else l = mid + 1;
    }
    return l;
}

int main() 
{
    scanf("%d", &t);
    while (t--) {
        scanf("%d%d", &n, &m);
        build(1, 1, n);
        int op, x, y;
        while (m--) {
            scanf("%d%d%d", &op, &x, &y);
            x++;
            if (op == 1) {
                int cnt = query(1, x, n);
                if (!cnt) puts("Can not put any one.");
                else {
                    int l = search(x, 1);
                    int r = search(x, min(cnt, y));
                    update(1, l, r, 0);
                    printf("%d %d\n", l - 1, r - 1);
                }
            }
            else if (op == 2) {
                y++;
                printf("%d\n", y - x + 1 - query(1, x, y));
                update(1, x, y, 1);
            }
        }
        puts("");
    }
    return 0;
}

13. HDU4553 约会安排

题目链接

题意：长度为 n 的区间，m 个操作：D x: 请求占用长度为 x 的连续区间，返回区间开始位置；N x: 请求占用长度为 x 的连续区间，如果没找到，可以忽略 D 的请求再寻找；S x y: 清空 [x, y] 占用部分。

??建 2 棵线段树维护最长连续区间，分别表示只有女神，以及既可以屌丝又可以女神，函数增加表示线段树的参数，注意输出标点符号是英文的。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, N = 1e5 + 5;

struct Node {
    int l, r;
    int ll, rl, ml, tag;
    inline int length() { return r - l + 1; }
}ds[N<<2], ns[N<<2];

int t, n, m;
char str[10];

void push_up(Node tree[], int rt) {
    tree[rt].ll = tree[rt<<1].ll, tree[rt].rl = tree[rt<<1|1].rl;
    if (tree[rt].ll == tree[rt<<1].length()) tree[rt].ll += tree[rt<<1|1].ll;
    if (tree[rt].rl == tree[rt<<1|1].length()) tree[rt].rl += tree[rt<<1].rl;
    tree[rt].ml = max(tree[rt<<1].rl + tree[rt<<1|1].ll, max(tree[rt<<1].ml, tree[rt<<1|1].ml));
}

void push_down(Node tree[], int rt) {
    if (~tree[rt].tag) {
        tree[rt<<1].tag = tree[rt<<1|1].tag = tree[rt].tag;
        tree[rt<<1].ll = tree[rt<<1].rl = tree[rt<<1].ml = tree[rt].tag ? 0 : tree[rt<<1].length();
        tree[rt<<1|1].ll = tree[rt<<1|1].rl = tree[rt<<1|1].ml = tree[rt].tag ? 0 : tree[rt<<1|1].length();
        tree[rt].tag = -1;
    }
}

void build(Node tree[], int rt, int l, int r) {
    tree[rt].l = l, tree[rt].r = r;
    tree[rt].ll = tree[rt].rl = tree[rt].ml = r - l + 1;
    tree[rt].tag = -1;
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(tree, rt<<1, l, mid);
    build(tree, rt<<1|1, mid + 1, r);
}

void update(Node tree[], int rt, int l, int r, int v) {
    if (l <= tree[rt].l && r >= tree[rt].r) {
        tree[rt].tag = v;
        tree[rt].ll = tree[rt].rl = tree[rt].ml = v ? 0 : tree[rt].length();
        return;
    }
    push_down(tree, rt);
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if (l <= mid) update(tree, rt<<1, l, r, v);
    if (r > mid) update(tree, rt<<1|1, l, r, v);
    push_up(tree, rt);
}

int query(Node tree[], int rt, int v) {
    if (tree[rt].ml < v) return 0;
    if (tree[rt].l == tree[rt].r) return tree[rt].l;
    push_down(tree, rt);
    if (tree[rt<<1].ml >= v) return query(tree, rt<<1, v);
    if (tree[rt<<1].rl + tree[rt<<1|1].ll >= v) return tree[rt<<1].r - tree[rt<<1].rl + 1;
    return query(tree, rt<<1|1, v);
}

int main()
{
    scanf("%d", &t);
    for (int cas = 1; cas <= t; ++cas) {
        scanf("%d%d", &n, &m);
        build(ds, 1, 1, n);
        build(ns, 1, 1, n);
        printf("Case %d:\n", cas);
        int x, y;
        while (m--) {
            scanf("%s%d", str, &x);
            if (str[0] == ‘D‘) {
                y = query(ds, 1, x);
                if (y) {
                    printf("%d,let‘s fly\n", y);
                    update(ds, 1, y, y + x - 1, 1);
                }
                else puts("fly with yourself");
            }
            else if (str[0] == ‘N‘) {
                y = query(ds, 1, x);
                if (y) {
                    printf("%d,don‘t put my gezi\n", y);
                    update(ds, 1, y, y + x - 1, 1);
                    update(ns, 1, y, y + x - 1, 1);
                }
                else {
                    y = query(ns, 1, x);
                    if (y) {
                        printf("%d,don‘t put my gezi\n", y);
                        update(ds, 1, y, y + x - 1, 1);
                        update(ns, 1, y, y + x - 1, 1);
                    }
                    else puts("wait for me");
                }
            }
            else if (str[0] == ‘S‘) {
                scanf("%d", &y);
                update(ds, 1, x, y, 0);
                update(ns, 1, x, y, 0);
                puts("I am the hope of chinese chengxuyuan!!");
            }
        }
    }
    return 0;
}

扫描线

接下来几题会涉及到扫描线，建议先学习 OIWiki-扫描线

14. POJ1177 Picture

题目链接

题意：求 n 个矩形的周长并。

??扫描线经典题。线段按 y 升序排序，按照 x 轴建立线段树，线段树维护区间完全覆盖次数 cnt，连续区间个数 num，覆盖长度 len，左右端点是否覆盖 lf、rf。

参考链接

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <map>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, N = 2e4 + 5;

struct Line {
    int h, l, r, f;
    Line() {}
    Line(int h, int l, int r, int f) : h(h), l(l), r(r), f(f) {}
    bool operator < (const Line &b) const {
        return h < b.h;
    }
}line[N];

struct Node {
    int l, r, cnt;
    int num, len;
    bool lf, rf;
}tree[N<<2];

int n, ans, pre;
int x[N];
map<int, int> mp;

void push_up(int rt) {
    if (tree[rt].cnt) {
        tree[rt].num = tree[rt].lf = tree[rt].rf = 1;
        tree[rt].len = x[tree[rt].r+1] - x[tree[rt].l];
    }
    else if (tree[rt].l == tree[rt].r) tree[rt].len = tree[rt].num = tree[rt].lf = tree[rt].rf = 0;
    else {
        tree[rt].len = tree[rt<<1].len + tree[rt<<1|1].len;
        tree[rt].num = tree[rt<<1].num + tree[rt<<1|1].num;
        if (tree[rt<<1].rf && tree[rt<<1|1].lf) --tree[rt].num;
        tree[rt].lf = tree[rt<<1].lf;
        tree[rt].rf = tree[rt<<1|1].rf;
    }
}

void build(int rt, int l, int r) {
    tree[rt].l = l, tree[rt].r = r;
    tree[rt].cnt = tree[rt].num = tree[rt].len = 0;
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(rt<<1, l, mid);
    build(rt<<1|1, mid + 1, r);
}

void update(int rt, int l, int r, int k) {
    if (l <= tree[rt].l && r >= tree[rt].r) {
        tree[rt].cnt += k;
        push_up(rt);
        return;
    }
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if (l <= mid) update(rt<<1, l, r, k);
    if (r > mid) update(rt<<1|1, l, r, k);
    push_up(rt);
}

int main() 
{
    scanf("%d", &n);
    int x1, y1, x2, y2;
    for (int i = 1; i <= n; ++i) {
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        line[i*2-1] = Line(y1, x1, x2, 1);
        line[i*2] = Line(y2, x1, x2, -1);
        x[2*i-1] = x1;
        x[2*i] = x2;
    }
    n <<= 1;
    sort(line + 1, line + n + 1);
    sort(x + 1, x + n + 1);
    int m = unique(x + 1, x + n + 1) - (x + 1);
    for (int i = 1; i <= m; ++i) mp[x[i]] = i;
    build(1, 1, m - 1);
    for (int i = 1; i <= n; ++i) {
        int l = mp[line[i].l], r = mp[line[i].r] - 1;
        update(1, l, r, line[i].f);
        ans += abs(tree[1].len - pre);
        pre = tree[1].len;
        ans += tree[1].num * (line[i+1].h - line[i].h) << 1; // 竖直周长
    }
    printf("%d\n", ans);
    return 0;
}

15. HDU1255 覆盖的面积

题目链接

题意：\(n(1\le n\le1000)\) 个矩形，求覆盖 2 次及以上的矩形面积并。

??稍微修改一下扫描线模板，维护结点被竖直线段完全覆盖次数 cnt，覆盖一次 x 方向长度 len1, 覆盖 2 次及以上 x 方向长度 len2。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <map>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, N = 2005;

struct Line {
    double h, l, r;
    int f;
    Line() {}
    Line(double h, double l, double r, int f) : h(h), l(l), r(r), f(f) {}
    bool operator < (const Line &b) const {
        return h < b.h;
    }
}line[N];

struct Node {
    int l, r, cnt;
    double len1, len2;
}tree[N<<2];

int t, n;
double x[N];
map<double, int> mp;

void push_up(int rt) {
    if (tree[rt].cnt > 1) {
        tree[rt].len1 = 0;
        tree[rt].len2 = x[tree[rt].r+1] - x[tree[rt].l];
    }
    else if (tree[rt].cnt == 1) {
        if (tree[rt].l == tree[rt].r) tree[rt].len2 = 0;
        else tree[rt].len2 = tree[rt<<1].len2 + tree[rt<<1].len1 + tree[rt<<1|1].len2 + tree[rt<<1|1].len1;
        tree[rt].len1 = (x[tree[rt].r+1] - x[tree[rt].l]) - tree[rt].len2;
    }
    else {
        if (tree[rt].l == tree[rt].r) tree[rt].len1 = tree[rt].len2 = 0;
        else {
            tree[rt].len1 = tree[rt<<1].len1 + tree[rt<<1|1].len1;
            tree[rt].len2 = tree[rt<<1].len2 + tree[rt<<1|1].len2;
        }
    }
}

void build(int rt, int l, int r) {
    tree[rt].l = l, tree[rt].r = r, tree[rt].cnt = 0;
    tree[rt].len1 = tree[rt].len2 = 0;
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(rt<<1, l, mid);
    build(rt<<1|1, mid + 1, r);
}

void update(int rt, int l, int r, int k) {
    if (l <= tree[rt].l && r >= tree[rt].r) {
        tree[rt].cnt += k;
        push_up(rt);
        return;
    }
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if (l <= mid) update(rt<<1, l, r, k);
    if (r > mid) update(rt<<1|1, l, r, k);
    push_up(rt);
}

int main() 
{
    scanf("%d", &t);
    while (t--) {
        scanf("%d", &n);
        double x1, y1, x2, y2;
        for (int i = 1; i <= n; ++i) {
            scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
            line[i*2-1] = Line(y1, x1, x2, 1);
            line[i*2] = Line(y2, x1, x2, -1);
            x[i*2-1] = x1;
            x[i*2] = x2;
        }
        n <<= 1;
        sort(line + 1, line + n + 1);
        sort(x + 1, x + n + 1);
        int m = unique(x + 1, x + n + 1) - (x + 1);
        for (int i = 1; i <= m; ++i) mp[x[i]] = i;
        build(1, 1, m - 1);
        double ans = 0;
        for (int i = 1; i <= n; ++i) {
            int l = mp[line[i].l], r = mp[line[i].r] - 1;
            update(1, l, r, line[i].f);
            ans += tree[1].len2 * (line[i+1].h - line[i].h);
        }
        printf("%.2lf\n", ans);
    }
    return 0;
}

16. HDU1542 Atlantis

题目链接

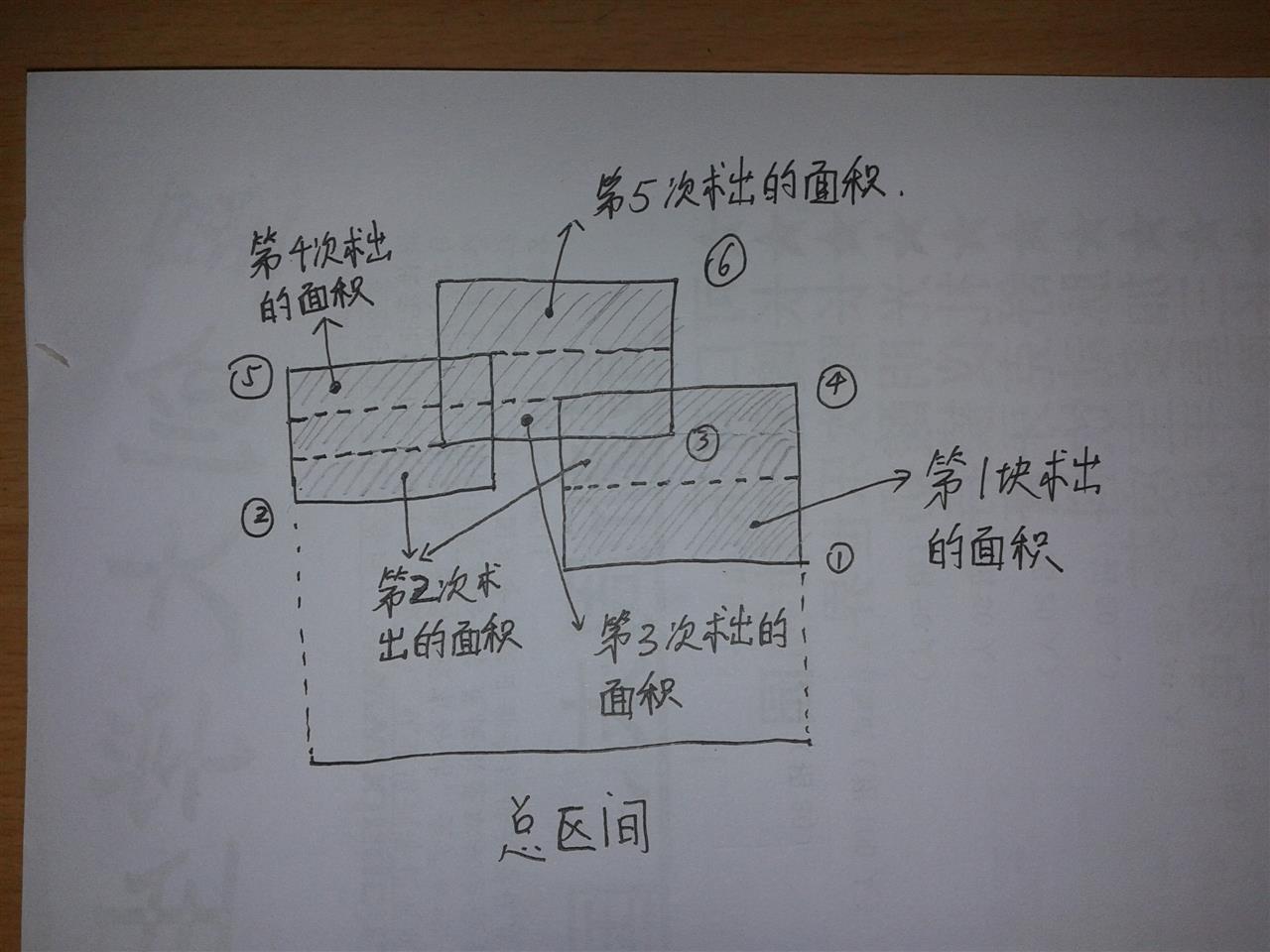
题意：求 \(n(1\le n\le 100)\) 个矩形的面积并。

??看这张别人画的图就明白了

技术图片

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <map>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, N = 105;

struct Line {
    double h, l, r;
    int f;
    Line() {}
    Line(double h, double l, double r, int f) : h(h), l(l), r(r), f(f) {}
    bool operator < (const Line &b) const {
        return h < b.h;
    }
}line[N<<1];

struct Node {
    int l, r, cnt;
    double len;
}tree[N<<3];

int n, cas, tot;
double x[N<<1];
map<double, int> mp;

void push_up(int rt) {
    if (tree[rt].cnt) tree[rt].len = x[tree[rt].r+1] - x[tree[rt].l];
    else if (tree[rt].l == tree[rt].r) tree[rt].len = 0;
    else tree[rt].len = tree[rt<<1].len + tree[rt<<1|1].len;
}

void build(int rt, int l, int r) {
    tree[rt].l = l, tree[rt].r = r;
    tree[rt].cnt = 0, tree[rt].len = 0;
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(rt<<1, l, mid);
    build(rt<<1|1, mid + 1, r);
}

void update(int rt, int l, int r, int k) {
    if (l <= tree[rt].l && r >= tree[rt].r) {
        tree[rt].cnt += k;
        push_up(rt);
        return;
    }
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if (l <= mid) update(rt<<1, l, r, k);
    if (r > mid) update(rt<<1|1, l, r, k);
    push_up(rt);
}

int main() 
{
    while (scanf("%d", &n), n) {
        double x1, x2, y1, y2;
        for (int i = 1; i <= n; ++i) {
            scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
            line[i*2-1] = Line(y1, x1, x2, 1);
            line[i*2] = Line(y2, x1, x2, -1);
            x[2*i-1] = x1;
            x[2*i] = x2;
        }
        n <<= 1;
        sort(line + 1, line + n + 1);
        sort(x + 1, x + n + 1);
        int m = unique(x + 1, x + n + 1) - (x + 1);
        for (int i = 1; i <= m; ++i) mp[x[i]] = i;
        build(1, 1, m - 1);
        double ans = 0;
        for (int i = 1; i <= n; ++i) {
            int l = mp[line[i].l], r = mp[line[i].r] - 1;
            update(1, l, r, line[i].f);
            ans += tree[1].len * (line[i+1].h - line[i].h);
        }
        printf("Test case #%d\nTotal explored area: %.2lf\n\n", ++cas, ans);
    }
    return 0;
}

17. HDU3642 Get The Treasury

题目链接

题意：\(n(1\le n\le1000)\) 个长方体，求相交 3 次及以上部分的体积。

??\(z\in[-500,500]\)，枚举 \(z_i\) 在 \([z_i,z_{i+1})\) 用扫描线转化为二维。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <map>
using namespace std;

#define debug(x) cout << #x << " is " << x << endl
#define inc(i, a, b) for (int i = a; i <= b; ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f, N = 2005;

struct Plane {
    int y, x1, z1, x2, z2, f;
    Plane() {}
    Plane(int y, int x1, int z1, int x2, int z2, int f) : y(y), x1(x1), z1(z1), x2(x2), z2(z2), f(f) {}
    bool operator < (const Plane &b) const {
        return y < b.y;
    }
}plane[N], tmp[N];

struct Node {
    int l, r, cnt;
    int len1, len2, len3;
}tree[N<<2];

int t, n;
int x[N], z[N];
map<int, int> mp;

void push_up(int rt) {
    if (tree[rt].cnt) tree[rt].len1 = x[tree[rt].r+1] - x[tree[rt].l];
    else if (tree[rt].l == tree[rt].r) tree[rt].len1 = 0;
    else tree[rt].len1 = tree[rt<<1].len1 + tree[rt<<1|1].len1;

    if (tree[rt].cnt >= 2) tree[rt].len2 = x[tree[rt].r+1] - x[tree[rt].l];
    else if (tree[rt].l == tree[rt].r) tree[rt].len2 = 0;
    else if (tree[rt].cnt == 1) tree[rt].len2 = tree[rt<<1].len1 + tree[rt<<1|1].len1;
    else if (!tree[rt].cnt) tree[rt].len2 = tree[rt<<1].len2 + tree[rt<<1|1].len2;

    if (tree[rt].cnt >= 3) tree[rt].len3 = x[tree[rt].r+1] - x[tree[rt].l];
    else if (tree[rt].l == tree[rt].r) tree[rt].len3 = 0;
    else if (tree[rt].cnt == 2) tree[rt].len3 = tree[rt<<1].len1 + tree[rt<<1|1].len1;
    else if (tree[rt].cnt == 1) tree[rt].len3 = tree[rt<<1].len2 + tree[rt<<1|1].len2;
    else if (!tree[rt].cnt) tree[rt].len3 = tree[rt<<1].len3 + tree[rt<<1|1].len3;
}

void build(int rt, int l, int r) {
    tree[rt].l = l, tree[rt].r = r, tree[rt].cnt = 0;
    tree[rt].len1 = tree[rt].len2 = tree[rt].len3 = 0;
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(rt<<1, l, mid);
    build(rt<<1|1, mid + 1, r);
}

void update(int rt, int l, int r, int k) {
    if (l <= tree[rt].l && r >= tree[rt].r) {
        tree[rt].cnt += k;
        push_up(rt);
        return;
    }
    int mid = (tree[rt].l + tree[rt].r) >> 1;
    if (l <= mid) update(rt<<1, l, r, k);
    if (r > mid) update(rt<<1|1, l, r, k);
    push_up(rt);
}

int main() 
{
    scanf("%d", &t);
    for (int cas = 1; cas <= t; ++cas) {
        scanf("%d", &n);
        int x1, x2, y1, y2, z1, z2;
        for (int i = 1; i <= n; ++i) {
            scanf("%d%d%d%d%d%d", &x1, &y1, &z1, &x2, &y2, &z2);
            plane[i*2-1] = Plane(y1, x1, z1, x2, z2, 1);
            plane[i*2] = Plane(y2, x1, z1, x2, z2, -1);
            x[i*2-1] = x1;
            x[i*2] = x2;
            z[i*2-1] = z1;
            z[i*2] = z2;
        }
        n <<= 1;
        sort(x + 1, x + n + 1);
        sort(z + 1, z + n + 1);
        int m1 = unique(x + 1, x + n + 1) - (x + 1);
        int m2 = unique(z + 1, z + n + 1) - (z + 1);
        for (int i = 1; i <= m1; ++i) mp[x[i]] = i;
        n >>= 1;
        ll ans = 0;
        for (int i = 1; i < m2; ++i) {
            build(1, 1, m1 - 1);
            int tot = 0;
            for (int j = 1; j <= n; ++j) {
                if (plane[j*2-1].z1 <= z[i] && plane[j*2-1].z2 > z[i]) {
                    tmp[++tot] = plane[j*2-1];
                    tmp[++tot] = plane[j*2];
                }
            }
            sort(tmp + 1, tmp + tot + 1);
            ll res = 0;
            for (int j = 1; j < tot; ++j) {
                int l = mp[tmp[j].x1], r = mp[tmp[j].x2] - 1;
                update(1, l, r, tmp[j].f);
                res += (ll)tree[1].len3 * (tmp[j+1].y - tmp[j].y);
            }
            ans += res * (z[i+1] - z[i]);
        }
        printf("Case %d: %lld\n", cas, ans);
    }
    return 0;
}

[kuangbin带你飞]专题七 线段树

标签：初始   延迟标记   最大连续   之间   tin   端点   add   geo   algo   

原文地址：https://www.cnblogs.com/2inf/p/13868482.html
踩
(0)
赞
(0)
   
举报
评论 一句话评论（0）
登录后才能评论！
分享档案
更多>
2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)
周排行
mamicode.com排行更多图片
更多
友情链接
兰亭集智   国之画   百度统计   站长统计   阿里云   chrome插件   新版天听网
关于我们 - 联系我们 - 留言反馈
© 2014 mamicode.com 版权所有  联系我们:gaon5@hotmail.com
迷上了代码！