2. A Distributional Perspective on Reinforcement Learning

标签：lob   http   图片   距离   value   https   fixed   方法   函数   

本文主要研究了分布式强化学习，利用价值分布(value distribution)的思想，求出回报\(Z\)的概率分布，从而取代期望值(即\(Q\)值)。

Q-Learning

Q-Learning的目标是近似Q函数，即在策略\(\pi\)下回报\(Z_t\)的期望值：

Q-Learning的核心是Bellman方程。它可以通过时序差分学习迭代更新Q函数

然后，最小化估计项\(Q(s,a)\)和目标项\(r+\gamma \max_{a^\prime}Q(s^\prime,a^\prime)\)的均方误差损失

通过假设目标\(r+\gamma \max_{a^\prime}Q(s^\prime,a^\prime)\)为定量，最小化公式(2)使\(Q(s,a)\)朝目标方向移动来优化网络。

Distributional RL

对于给定状态\(s\)和动作\(a\)，智能体获得的回报\(Z(s,a)\)是服从某种分布的随机变量，传统的方法是利用它的期望值来优化策略。

而分布式强化学习的思想是直接作用在回报\(Z(s,a)\)的价值分布上，而不是它的期望。

学习\(Z(s,a)\)的概率分布，以此取代它的期望函数\(Q(s,a)\)，有以下几个优势：

1. 学习到的概率分布所含信息比期望值要丰富。当两个动作期望值相同时，可以选择方差较小的动作
2. 针对一些稀疏奖励的场景，使用价值分布可以有效缓解
3. 只考虑期望值，可能会忽略在某一状态下回报显著的动作，导致学习陷入次优策略

Value Distribution

使用一个随机变量\(Z(s,a)\)替代\(Q(s,a)\)，\(Z(s,a)\)用于表示回报的分布，被称为价值分布(value distribution)，它们的关系式为

\(s_t\sim P(\cdot|s_{t-1},a_{t-1}),a_t\sim\pi(\cdot|x_t),s_0=x,a_0=a\)
同时，可以推出当前状态和下一状态的\(Z\)都服从同一分布\(D\)，因此，定义transition算子\(\mathcal{P}^\pi\)：

\(s^\prime\sim P(\cdot|s,a),a^\prime\sim \pi(\cdot|s^\prime)\)，\(P^\pi:Z\to Z\)

Policy Evaluation

根据公式(1)的Bellman方程，可以定义Bellman算子\(\mathcal{T}^\pi\)，如下

再结合公式(3)，可以推出Bellman方程的分布式版本

上式表示\(Z(s,a)\)和\(Z(s^\prime,a^\prime)\)都服从同一分布\(D\)。

衡量两个价值分布距离时，不光要考虑\(Z\)本身的随机性，还需要考虑输入自变量\(s\)和\(a\)。因此，该距离定义为：

\(s^\prime \sim p(\cdot|s,a)\)
【注】上式式代替公式(2)来优化网络，但优化策略时仍然使用期望\(Q(s,a)\)。论文用Wassertein metric作为距离度量，并证明了在该度量下，通过分布式Bellman方程更新，最终都能收敛于真实的价值分布，即Bellman算子\(\mathcal{T}^\pi:Z\to Z\)可以看作\(\gamma\)收缩：\(\text{dist}(\mathcal{T}Q_1,\mathcal{T}Q_2)\le \gamma \text{dist}(Q_1,Q_2)\)，由于\(Q^\pi\)是唯一不动点，即\(\mathcal{T}Q=Q\Leftrightarrow Q=Q^\pi\)，所以在不考虑近似误差的情况下，使\(\mathcal{T}^\infty Q=Q^\pi\)。

Control

最优策略的定义是使回报期望最大的策略，因此，最优策略对应的价值分布也应是最优的。在只考虑期望的时候，最优策略是没有歧义的，也就是说，选择的最优价值函数只有一个，即唯一不动点\(Q^\pi\)(Banach‘s Fixed Point Theorem)。但考虑价值分布时，会存在期望值相同的同等最优价值分布，因此存在一族不稳定的最优价值分布。论文中对所有最优策略排序，只允许存在一个最优策略，即可产生一个唯一不动点\(Z^{\pi^*}\)。

Implement

本文提出通过多个支持构建的离散分布表示价值分布，且\(Z\)和\(Z‘\)共享相同的离散支持集。这种离散分布的优点是表现力强(即它可以表示任何类型的分布，不限于高斯分布)。

此外，因为Wassertein距离作为度量难以实现，所以改用交叉熵损失优化网络。

实现原理：

1. 构建\(Z(s^\prime,a^\prime)\)价值分布模型，将价值分布的区间\([V_\text{MIN},V_\text{MAX}]\)分为N等分，每份间距为\(\triangle z=\frac{V_\text{MAX}-V_\text{MIN}}{N-1}\)，得到一个离散支持的原子集\(\{z_i=V_{\rm MIN}+i \triangle z,0\le i<N \}\)，图示如下

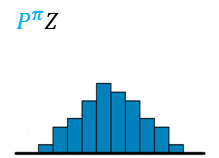
??然后，用参数化模型\(\theta:\mathcal{S}\times\mathcal{A}\to\mathbb{R}^N\)得到原子概率

2. 对\(Z(s‘,a‘)\)先用\(\gamma\)进行缩放，再用\(R\)进行位移，得到目标分布

??图示如下

3. \(\gamma\)是折扣回报，且奖励值不一定为\(\triangle z\)的整数倍，所以不能保证通过Bellman算子更新所得的\(Z(s^\prime,a^\prime)\)落在更新前相同值的原子上，因此，需要利用\(\Phi\)投影。
   将样本Bellman更新\(\mathcal{\hat T} Z_\theta\)投影到\(Z_\theta\)的支持上，有效地将Bellman更新减少到多类别分类。给出采样转移\((s,a,r,s^\prime)\)，可以计算出每个原子\(z_j\)的Bellman更新\(\mathcal{\hat T} z_j\doteq r+\gamma z_j\)，然后分配其概率\(p_j(s^\prime,\pi(s^\prime))\)。因此，投影更新\(\Phi \hat{\mathcal{T}} Z_\theta(s,a)\)的第\(i\)个组成部分为

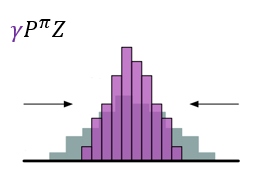
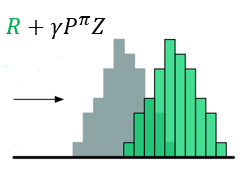
??其中，\([\cdot]_a^b\)将参数限制在范围\([a,b]\)，\(\pi\)是贪心策略。图示如下

4. 使用KL散度来约束两个分布

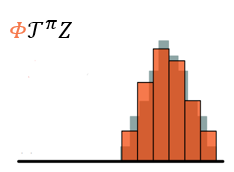
??最终，得到交叉熵损失函数

C51算法：

Append

1. Wasserstein Metric
它用于衡量概率分布的累积分布函数距离。\(p\)-Wasserstein度量\(W_p(p\in[1,\infty])\)可以看作是逆累积分布函数的\(L^p\)度量。假设两个分布为\(U\)和\(V\)，则\(p\)-Wasserstein距离为

对于随机变量\(Y\)，它的累积分布函数为\(F_Y(y)=\Pr(Y\le y)\)，对应的逆累积分布函数为

【注】对于\(p=\infty\)，\(W_\infty(Y,U)=\sup_{\mathcal{w}\in [0,1]|F^{-1}_Y(\mathcal{w})-F^{-1}_U(\mathcal{w})|}\)

2. KL散度与交叉熵损失
对于离散情况，\(p\)和\(q\)分布的KL散度为

References

Marc G. Bellemare, Will Dabney, Rémi Munos. A Distributional Perspective on Reinforcement Learning. 2017.
Distributional Bellman and the C51 Algorithm
Distributional RL

2. A Distributional Perspective on Reinforcement Learning

标签：lob   http   图片   距离   value   https   fixed   方法   函数   

原文地址：https://www.cnblogs.com/HughCai/p/13845571.html