作者|PROCRASTINATOR
编译|VK
来源|Analytics Vidhya
了解类权重优化是如何工作的,以及如何在logistic回归或任何其他算法中使用sklearn实现相同的方法
了解如何在不使用任何采样方法的情况下,通过修改类权重可以克服类不平衡数据的问题
机器学习中的分类问题是我们给出了一些输入(独立变量),并且我们必须预测一个离散目标。离散值的分布极有可能是非常不同的。由于每个类的差异,算法往往偏向于现有的大多数值,而对少数值的处理效果不好。
类频率的这种差异影响模型的整体可预测性。
在这些问题上获得良好的准确度并不难,但并不意味着模型是良好的。我们需要检查这些模型的性能是否具有任何商业意义或有任何价值。这就是为什么理解问题和数据是非常必要的,这样你就可以使用正确的度量并使用适当的方法优化它。
什么是类别失衡?
为什么要处理类别不平衡?
什么是类别权重?
logistic回归中的类权重
Python实现
进一步提高分数的技巧
类不平衡是机器学习分类问题中出现的一个问题。它只说明目标类的频率高度不平衡,即其中一个类的频率与现有的其他类相比非常高。换句话说,对目标中的大多数类存在偏见。
假设我们考虑一个二分类,其中大多数目标类有10000个,而少数目标类只有100个。在这种情况下,比率为100:1,即每100个多数类,就只有一个少数类。这个问题就是我们所说的类别失衡。我们可以找到这些数据的一般领域有欺诈检测、流失预测、医疗诊断、电子邮件分类等。
我们将在医学领域中处理一个数据集,以正确理解类不平衡。在这里,我们必须根据给定的属性(独立变量)来预测一个人是否会患上心脏病。为了跳过数据的清理和预处理,我们使用的是数据的已清理版本。
在下面的图像中,你可以看到目标变量的分布。
#绘制目标的条形图
plt.figure(figsize=(10,6))
g = sns.barplot(data[‘stroke‘], data[‘stroke‘], palette=‘Set1‘, estimator=lambda x: len(x) / len(data) )
#图的统计
for p in g.patches:
width, height = p.get_width(), p.get_height()
x, y = p.get_xy()
g.text(x+width/2,
y+height,
‘{:.0%}‘.format(height),
horizontalalignment=‘center‘,fontsize=15)
#设置标签
plt.xlabel(‘Heart Stroke‘, fontsize=14)
plt.ylabel(‘Precentage‘, fontsize=14)
plt.title(‘Percentage of patients will/will not have heart stroke‘, fontsize=16)
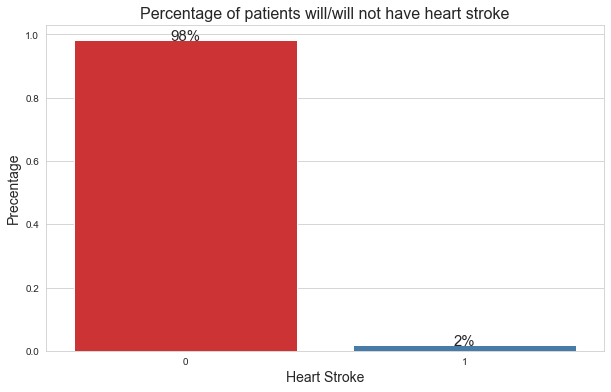
在这里,
0:表示患者没有心脏病。
1: 表示病人患了心脏病。
从分布上可以看出,只有2%的患者患有心脏病。所以,这是一个经典的类别失衡问题。
到目前为止,我们已经对类别失衡有了直觉。但是为什么需要克服这个问题,在使用这些数据建模时会产生什么问题?
大多数机器学习算法都假定数据在类中分布均匀。在类不平衡问题中,广泛的问题是算法将更偏向于预测大多数类别(在我们的情况下没有心脏病)。该算法没有足够的数据来学习少数类(心脏病)中的模式。
让我们以一个现实生活的例子来更好地理解这一点。
假设你已经从你的家乡搬到了一个新的城市,你在这里住了一个月。当你来到你的家乡,你会非常熟悉所有的地方,如你的家,路线,重要的商店,旅游景点等等,因为你在那里度过了你的整个童年。
但是到了新城市,你不会对每个地方的具体位置有太多的想法,走错路线迷路的几率会非常高。在这里,你的家乡是你的多数类,新城是少数类。
同样,这种情况也会发生在类别不平衡中。少数类关于你类的信息不充分,这就是为什么少数类会有很高的误分类错误。
注:为了检查模型的性能,我们将使用f1分数作为衡量标准,而不是准确度。
原因是如果我们建立一个愚蠢的模型,预测每一个新的训练数据为0(没有心脏病),即使这样,我们也会得到非常高的准确率,因为模型偏向大多数类。
在这里,模型非常精确,但对我们的问题陈述没有任何价值。这就是为什么我们将使用f1分数作为评估指标。F1分数只不过是精确度和召回率的调和平均值。但是,评估指标是根据业务问题和我们希望减少的错误类型来选择的。但是,f1分数是衡量类别不平衡问题的关键。
以下是f1分数公式:
f1 score = 2*(precision*recall)/(precision+recall)
让我们通过训练一个基于目标变量模式的模型来确认这一点,并检查我们得到的分数:
#利用目标模式训练模型
from sklearn.metrics import f1_score, accuracy_score, confusion_matrix
pred_test = []
for i in range (0, 13020):
pred_test.append(y_train.mode()[0])
#打印f1和准确度分数
print(‘The accuracy for mode model is:‘, accuracy_score(y_test, pred_test))
print(‘The f1 score for the model model is:‘,f1_score(y_test, pred_test))
#绘制混淆矩阵
conf_matrix(y_test, pred_test)
模式模型的准确度为:0.9819508448540707
模式模式的f1分数为:0.0
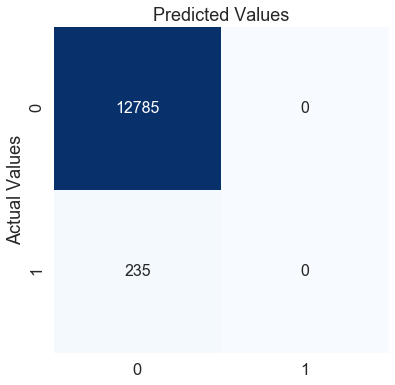
在这里,模型对测试数据的准确度为0.98,这是一个很好的分数。但另一方面,f1的分数为零,这表明该模型在少数类群体中表现不佳。我们可以通过查看混淆矩阵来确认这一点。
模式模型预测每个病人为0(无心脏病)。根据这个模型,无论病人有什么样的症状,他/她永远不会犯心脏病。使用这个模型有意义吗?
现在我们已经了解了什么是类不平衡以及它如何影响我们的模型性能,我们将把重点转移到类权重是什么以及类权重如何帮助改进模型性能。
大多数机器学习算法对有偏差的类数据不是很有用。但是,我们可以对现有的训练算法进行修改,以考虑到类的倾斜分布。这可以通过给予多数类别和少数类别不同的权重来实现。在训练阶段,权重的差异会影响类别的分类。其整体目的是通过设置更高的类权重,同时为多数类降低权重,以惩罚少数类的错误分类。
为了更清楚地说明这一点,我们将恢复我们之前考虑过的城市例子。
请这样想一想,上个月你在这个新城市度过,而不是在需要的时候出去,而是花了整整一个月的时间探索这个城市。整个月你花了更多的时间了解城市的路线和地点。给你更多的时间去研究将有助于你更好地了解这个新城市,并且减少迷路的机会。这正是类权重的工作原理。
在训练过程中,我们在算法的代价函数中赋予少数类更大的权重,使其能够对少数类提供更高的惩罚,使算法能够专注于减少少数类的误差。
注意:有一个阈值,你应该分别增加和减少少数类和多数类的类权重。如果给少数类赋予非常高的类权重,算法很可能会偏向少数类,并且会增加多数类中的错误。
大多数sklearn分类器建模库,甚至一些基于boosting的库,如LightGBM和catboost,都有一个内置的参数“class_weight”,这有助于我们优化少数类的得分,就像我们目前所学的那样。
默认情况下,class_weights 的值为“None”,即两个类的权重相等。除此之外,我们可以给它“balanced”或者传递一个包含两个类的人工设计权重的字典。
当类权重=‘平衡’时,模型会自动分配与其各自频率成反比的类权重。
更精确地说,计算公式为:
wj=n_samples / (n_classes * n_samplesj)
在这里,
wj是每个类的权重(j表示类)
n_samples是数据集中的样本或行总数
n_classes是目标中唯一类的总数
n_samplesj是相应类的总行数
对于我们的心脏案例:
n_samples= 43400, n_classes= 2(0&1), n_sample0= 42617, n_samples1= 783
0类的权重:
w0= 43400/(2*42617) = 0.509
1类的权重:
w1= 43400/(2*783) = 27.713
我希望这能让事情更清楚地表明,类别权重=‘balanced’有助于我们给予少数类别更高的权重,给多数类别较低的权重。
虽然在大多数情况下,将值作为“balanced”传递会产生很好的结果,但有时对于极端的类不平衡,我们可以尝试设计权重。稍后我们将了解如何在Python中找到类权重的最佳值。
我们可以通过在算法的代价函数中添加不同的类权重来修改每种机器学习算法,但这里我们将特别关注logistic回归。
对于logistic回归,我们使用对数损失作为成本函数。我们没有使用均方误差作为logistic回归的成本函数,因为我们使用sigmoid曲线作为预测函数,而不是拟合直线。
将sigmoid函数展平会导致一条非凸曲线,这使得代价函数具有大量的局部极小值,而用梯度下降法收敛到全局极小值是非常困难的。但是对数损失是一个凸函数,我们只有一个极小值可以收敛。
log损失公式:
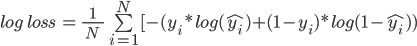
在这里,
N是值的数目
yi是目标类的实际值
yi是目标类的预测概率
让我们形成一个伪表,其中包含实际预测、预测概率和使用log损失公式计算的成本:
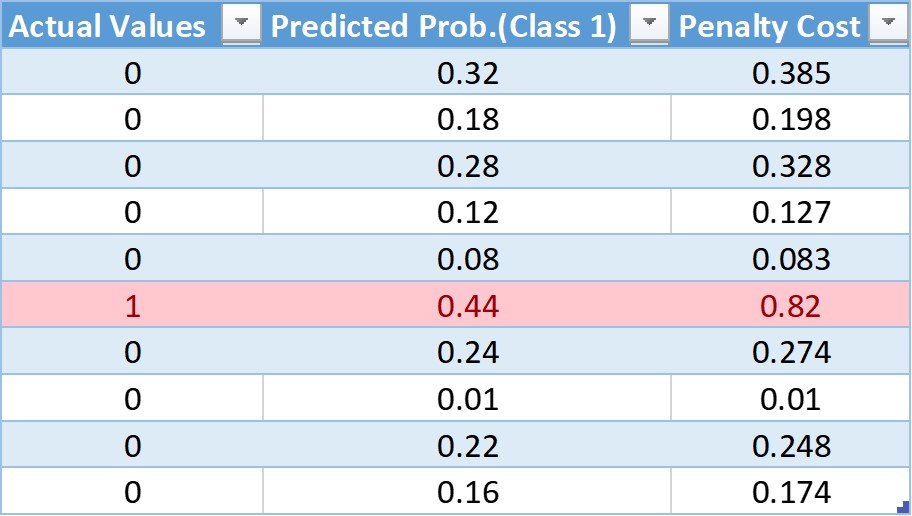
在这个表格中,我们有10个观察值,其中9个来自0类,9个来自1类。在下一篇专栏文章中,我们将给出每一次观察的预测概率。最后,利用对数损失公式,我们得到了成本惩罚。
将权重加入成本函数后,修改后的对数损失函数为:
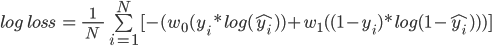
这里
w0是类0的类权重
w1是类1的类权重
现在,我们将添加权重,看看它会对成本惩罚产生什么影响。
对于权重值,我们将使用class_weights=‘balanced‘公式。
w0= 10/(2*1) = 5
w1= 10/(2*9) = 0.55
计算表中第一个值的成本:
Cost = -(5(0*log(0.32) + 0.55(1-0)*log(1-0.32))
= -(0 + 0.55*log(.68))
= -(0.55*(-0.385))
= 0.211
同样,我们可以计算每个观测值的加权成本,更新后的表为:
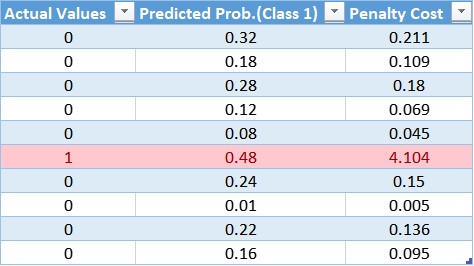
通过该表,我们可以确定对大多数类的成本函数应用了较小的权重,从而导致较小的误差值,进而减少了对模型系数的更新。一个更大的权重值应用到少数类的成本函数中,这会导致更大的误差计算,进而对模型系数进行更多的更新。这样,我们就可以改变模型的偏差,从而减少少数类的误差。
较小的权重会导致较小的惩罚和对模型系数的小更新
较大的权重会导致较大的惩罚和对模型系数的大量更新
在这里,我们将使用相同的心脏病数据来预测。首先,我们将训练一个简单的logistic回归,然后我们将实现加权logistic回归,类权重为“平衡”。最后,我们将尝试使用网格搜索来找到类权重的最佳值。我们试图优化的指标将是f1分数。
这里,我们使用sklearn库来训练我们的模型,我们使用默认的logistic回归。默认情况下,算法将为两个类赋予相等的权重。
#导入和训练模型
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(solver=‘newton-cg‘)
lr.fit(x_train, y_train)
#测试数据预测
pred_test = lr.predict(x_test)
#计算并打印f1分数
f1_test = f1_score(y_test, pred_test)
print(‘The f1 score for the testing data:‘, f1_test)
# 创建混淆矩阵的函数
def conf_matrix(y_test, pred_test):
# 创建混淆矩阵
con_mat = confusion_matrix(y_test, pred_test)
con_mat = pd.DataFrame(con_mat, range(2), range(2))
plt.figure(figsize=(6,6))
sns.set(font_scale=1.5)
sns.heatmap(con_mat, annot=True, annot_kws={"size": 16}, fmt=‘g‘, cmap=‘Blues‘, cbar=False)
#调用函数
conf_matrix(y_test, pred_test)
测试数据f1得分:0.0

在简单的logistic回归模型中,f1得分为0。通过观察混淆矩阵,我们可以确认我们的模型预测了每一个观察结果,因为不会发生心脏病。这个模型并不比我们前面创建的模式模型好。让我们试着给少数类增加一些权重,看看这是否有帮助。
我们在logistic回归算法中加入了类权重参数,传递的值是“balanced”。
#导入和训练模型
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(solver=‘newton-cg‘, class_weight=‘balanced‘)
lr.fit(x_train, y_train)
# 测试数据预测
pred_test = lr.predict(x_test)
# 计算并打印f1分数
f1_test = f1_score(y_test, pred_test)
print(‘The f1 score for the testing data:‘, f1_test)
#绘制混淆矩阵
conf_matrix(y_test, pred_test)
测试数据f1得分:0.10098851188885921
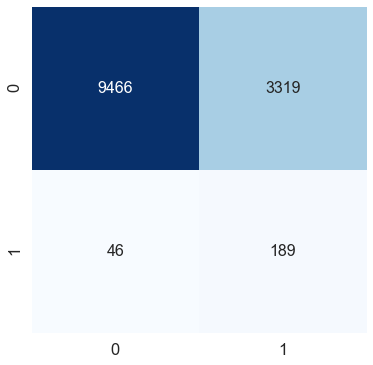
通过在logistic回归函数中添加一个单类权重参数,我们将f1分数提高了10%。我们可以在混淆矩阵中看到,尽管类0(无心脏病)的错误分类增加了,但模型可以很好地捕捉到类1(心脏病)。
我们可以通过改变类权重来进一步改进度量吗?
最后,我们尝试使用网格搜索来寻找得分最高的最优权重。我们将搜索0到1之间的权重。我们的想法是,如果我们给少数类别n作为权重,多数类别将得到1-n作为权重。
在这里,权重的大小并不是很大,但是多数类别和少数类别之间的权重比例将非常高。
例如:
w1 = 0.95
w0 = 1 – 0.95 = 0.05
w1:w0 = 19:1
因此,少数类别的权重将是多数类别的19倍。
from sklearn.model_selection import GridSearchCV, StratifiedKFold
lr = LogisticRegression(solver=‘newton-cg‘)
#设置类权重的范围
weights = np.linspace(0.0,0.99,200)
#为网格搜索创建字典网格
param_grid = {‘class_weight‘: [{0:x, 1:1.0-x} for x in weights]}
##用5倍网格搜索法拟合训练数据
gridsearch = GridSearchCV(estimator= lr,
param_grid= param_grid,
cv=StratifiedKFold(),
n_jobs=-1,
scoring=‘f1‘,
verbose=2).fit(x_train, y_train)
#绘制不同权重值的分数
sns.set_style(‘whitegrid‘)
plt.figure(figsize=(12,8))
weigh_data = pd.DataFrame({ ‘score‘: gridsearch.cv_results_[‘mean_test_score‘], ‘weight‘: (1- weights)})
sns.lineplot(weigh_data[‘weight‘], weigh_data[‘score‘])
plt.xlabel(‘Weight for class 1‘)
plt.ylabel(‘F1 score‘)
plt.xticks([round(i/10,1) for i in range(0,11,1)])
plt.title(‘Scoring for different class weights‘, fontsize=24)
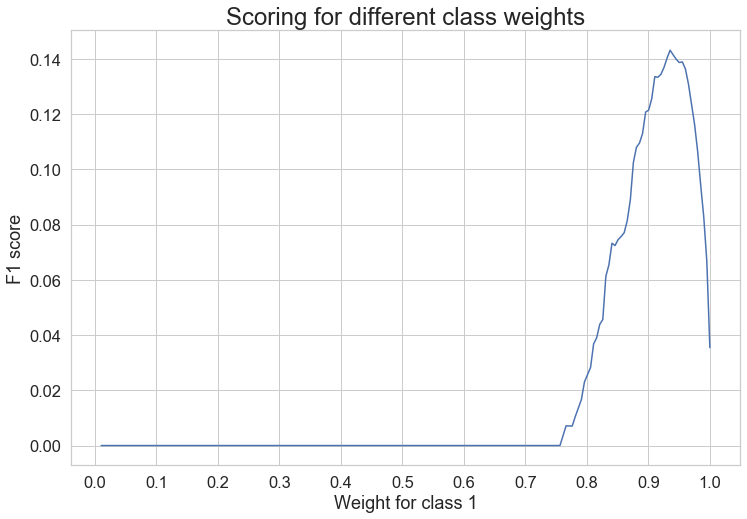
从图中我们可以看到少数类的最高值在0.93处达到峰值。
通过网格搜索,我们得到了最佳的类权重,0类(多数类)为0.06467,1类(少数类)为1:0.93532。
现在我们已经使用分层交叉验证和网格搜索获得了最佳类权重,我们将看到测试数据的性能。
#导入和训练模型
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(solver=‘newton-cg‘, class_weight={0: 0.06467336683417085, 1: 0.9353266331658292})
lr.fit(x_train, y_train)
# 测试数据预测
pred_test = lr.predict(x_test)
# 计算并打印f1分数
f1_test = f1_score(y_test, pred_test)
print(‘The f1 score for the testing data:‘, f1_test)
# 绘制混淆矩阵
conf_matrix(y_test, pred_test)
f1分数:0.15714644
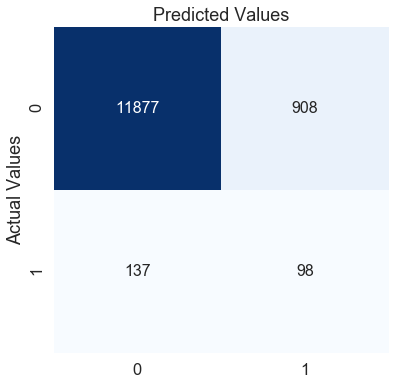
通过手动改变权重值,我们可以进一步提高f1分数约6%。混淆矩阵还表明,从之前的模型来看,我们能够更好地预测0类,但代价是我们的1类错误分类。这完全取决于业务问题或你希望减少的错误类型。在这里,我们的重点是提高f1分数,我们可以通过调整类别权重来做到这一点。
特征工程:为了简单起见,我们只使用了给定的自变量。你可以尝试创建新的特征
调整阈值:默认情况下,所有算法的阈值都是0.5。你可以尝试不同的阈值值,并可以通过使用网格搜索或随机化搜索来找到最佳值
使用高级算法:对于这个解释,我们只使用了logistic回归。你可以尝试不同的bagging 和boosting 算法。最后还可以尝试混合多种算法
我希望这篇文章能让你了解类权重如何帮助处理类不平衡问题,以及在python中实现它有多容易。
虽然我们已经讨论了类权重如何仅适用于logistic回归,但其他算法的思想都是相同的;只是每种算法用于最小化误差和优化少数类结果的代价函数的变化
原文链接:https://www.analyticsvidhya.com/blog/2020/10/improve-class-imbalance-class-weights/
欢迎关注磐创AI博客站:
http://panchuang.net/
sklearn机器学习中文官方文档:
http://sklearn123.com/
欢迎关注磐创博客资源汇总站:
http://docs.panchuang.net/
原文地址:https://www.cnblogs.com/panchuangai/p/13934205.html