标签:没有 arp 返回 示例 list insert ++ 重叠 max
给出一个无重叠的 ,按照区间起始端点排序的区间列表。
在列表中插入一个新的区间,你需要确保列表中的区间仍然有序且不重叠(如果有必要的话,可以合并区间)。
示例 1:
输入:intervals = [[1,3],[6,9]], newInterval = [2,5] 输出:[[1,5],[6,9]]
示例 2:
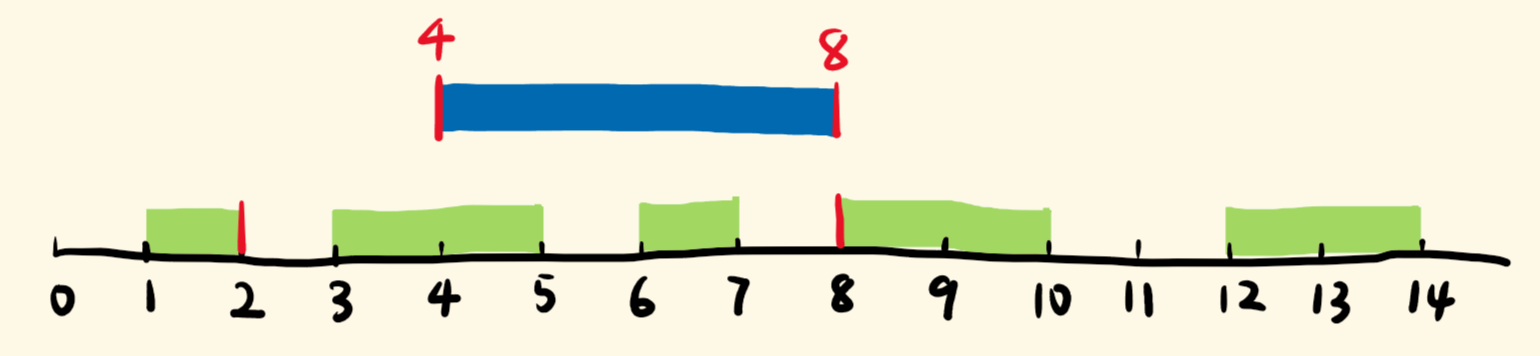
输入:intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8] 输出:[[1,2],[3,10],[12,16]] 解释:这是因为新的区间 [4,8] 与 [3,5],[6,7],[8,10] 重叠。
==================================================================================================
思路:既然是找重复区间,那么就可以先记录下新区间的左右边界。先将原列表中没有覆盖到的区间存进要返回的新list中,再去找覆盖到的区间。这样插入新区间左侧边界没有覆盖到的区间都已经进入到了输出列表,那么就默认接下来的区间都是可以覆盖到的。现在把判定改到右边,当列表中某区间的左边界小于等于插入区间的右边界,即说明该区间是被覆盖到的。这里用min来求最小的左边界,用max来求最大的右边界,这样求得的覆盖区间就是最大的了。然后将剩下没有覆盖到的、原列表中的区间加入到输出列表中返回即可。
class Solution { public int[][] insert(int[][] intervals, int[] newInterval) { //左右边界 int left = newInterval[0]; int right = newInterval[1]; int len = intervals.length; List<int[]> list = new ArrayList<>(); int i = 0;//指针指向原列表的区间 //找左边没覆盖到的区间 while (i < len && intervals[i][1] < left) { list.add(intervals[i]); i++; } //找覆盖到了的区间,min和max来获得左右最大边界 while (i < len && intervals[i][0] <= right) { left = Math.min(intervals[i][0], left); right = Math.max(intervals[i][1], right); i++; } int[] res = {left, right}; list.add(res); //将右边剩余的区间加入结果 while (i < len && intervals[i][0] > right) { list.add(intervals[i]); i++; } return list.toArray(new int[0][]); } }
标签:没有 arp 返回 示例 list insert ++ 重叠 max
原文地址:https://www.cnblogs.com/RS-Sakura/p/13926911.html