Leetcode1382.将二叉搜索树变平衡

标签：中序   push   size   roo   ack   inf   load   image   alt   

题目

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> orderseq; //存储中序遍历之后的有序序列
    void inorder_traversal(TreeNode* root) //中序遍历
    {
        if(root)
        {
            inorder_traversal(root->left);//左
            orderseq.push_back(root->val);//根
            inorder_traversal(root->right);//右
        }
    }
    TreeNode* build_tree(int low,int high)//根据index构造树，包前包后
    {
        if(low>high) //终点
            return NULL;
        else if(low==high)//终点
        {
            TreeNode* ans=new TreeNode(orderseq[low]);
            return ans;
        }
        else
        {
            int mid=(low+high)/2;
            TreeNode* ans=new TreeNode(orderseq[mid]);
            ans->left=build_tree(low,mid-1);
            ans->right=build_tree(mid+1,high);
            return ans;
        }
    }
    TreeNode* balanceBST(TreeNode* root) 
    {
        inorder_traversal(root);
        return build_tree(0,orderseq.size()-1);
    }
};```
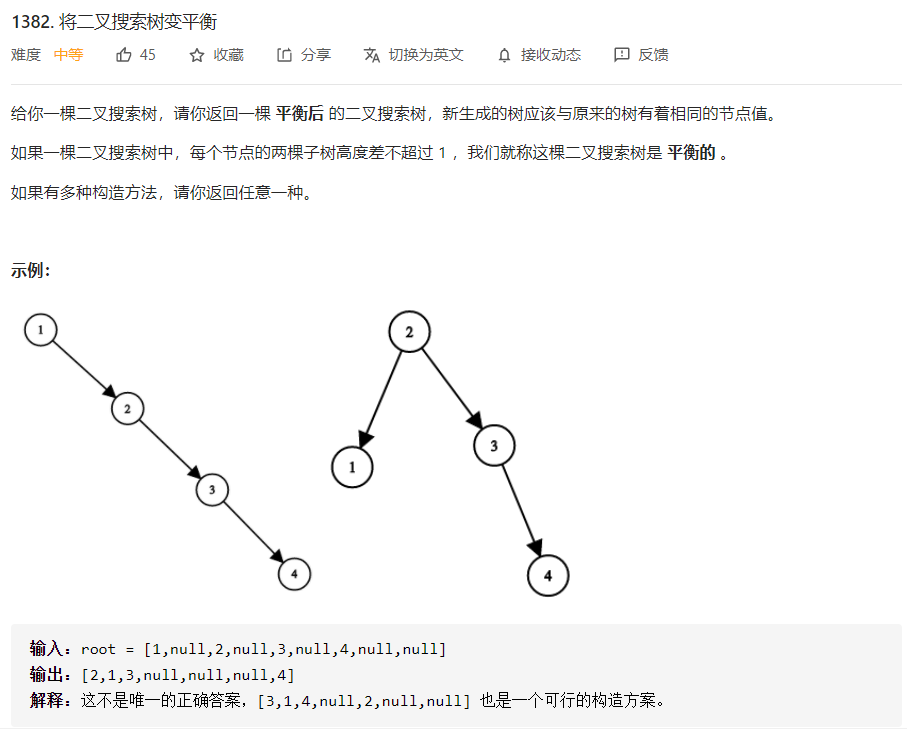
## 算法  
二叉搜索树右子树上的所有元素都比根节点大，左子树上的所有元素都比根节点小  

1.  运用中序遍历（左根右）将二叉搜索树转化为有序序列  
2.  选用有序序列的中间点为根节点，中间点左侧的为左子树，中间点右侧的为右子树  
3.  用有序序列index的方式（[low,high]，mid=(low+high)/2），考虑边界条件构造树

Leetcode1382.将二叉搜索树变平衡

标签：中序   push   size   roo   ack   inf   load   image   alt   

原文地址：https://www.cnblogs.com/ouyangyang/p/13949244.html