盛最多水的容器（leetcode-11）

标签：stream   names   ++   输入   两个指针   using   mes   tor   span   

题目

给你\(n\)个非负整数\(a_1，a_2，...，a_n\)每个数代表坐标中的一个点\((i, a_i)\)。在坐标内画\(n\)条垂直线，垂直线\(i\)的两个端点分别为\((i, a_i)\)和\((i, 0)\)。找出其中的两条线，使得它们与\(x\)轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器。

示例 1：
输入：[1,8,6,2,5,4,8,3,7]
输出：49

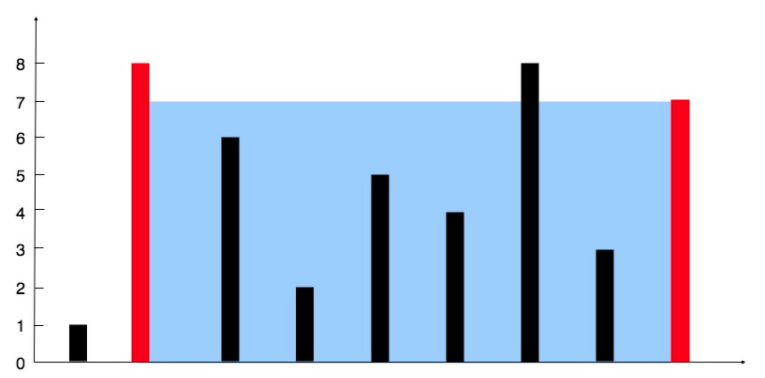
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：
输入：height = [1,1]
输出：1

示例 3：
输入：height = [4,3,2,1,4]
输出：16

示例 4：
输入：height = [1,2,1]
输出：2

提示：
$n = $height.length
\(2 <= n <= 3 * 10^4\)
\(0 <= height[i] <= 3 * 10^4\)

思路

看到这种连续区间的题目，首先想到双指针。（想到了双指针，没想到初始是指向两边的= =

从图和大致分析可以得出，我们希望找到两个又长，距离又远的隔板。先从最远的隔板开始扫描。左指针指向最左边，右指针指向最右边。然后慢慢缩小范围。直到找到两个指针指向同一隔板。

面积 = min（左隔板长度, 右隔板长度) * length。如果缩小长的那个，那么显然面积只会小不会大。而且我们的思想是找两个长隔板。所以扫描规则是每次往后（前）缩进短的那个隔板。

代码

# include <iostream>
# include <vector>
# include <algorithm>
using namespace std;
using ll = long long;
class Solution {
public:
    int maxArea(vector<int>& height) {
        int lp = 0, rp = height.size() - 1, ans = 0;
        while (lp < rp) {
            ans = max(ans, (rp - lp) * min(height[lp], height[rp]));
            if (height[lp] < height[rp]) lp++;
            else rp--;
        }
        return ans;
    }
};

盛最多水的容器（leetcode-11）

标签：stream   names   ++   输入   两个指针   using   mes   tor   span   

原文地址：https://www.cnblogs.com/destinyzk/p/13950848.html